0459. Repeated Substring Pattern (E)

Repeated Substring Pattern (E)

题目

Given a non-empty string check if it can be constructed by taking a substring of it and appending multiple copies of the substring together. You may assume the given string consists of lowercase English letters only and its length will not exceed 10000.

Example 1:

Input: "abab"
Output: True
Explanation: It's the substring "ab" twice.

Example 2:

Input: "aba"
Output: False

Example 3:

Input: "abcabcabcabc"
Output: True
Explanation: It's the substring "abc" four times. (And the substring "abcabc" twice.)

---

题意

判断一个字符串是否能有其中的一个子串重复多次得到。

思路

最简单的直接暴力遍历即可。

另一种比较好的方法是先用KMP算法的前半部分计算next数组，这样可以得到字符串s的最长公共前后缀。以字符串 abababab 为例：

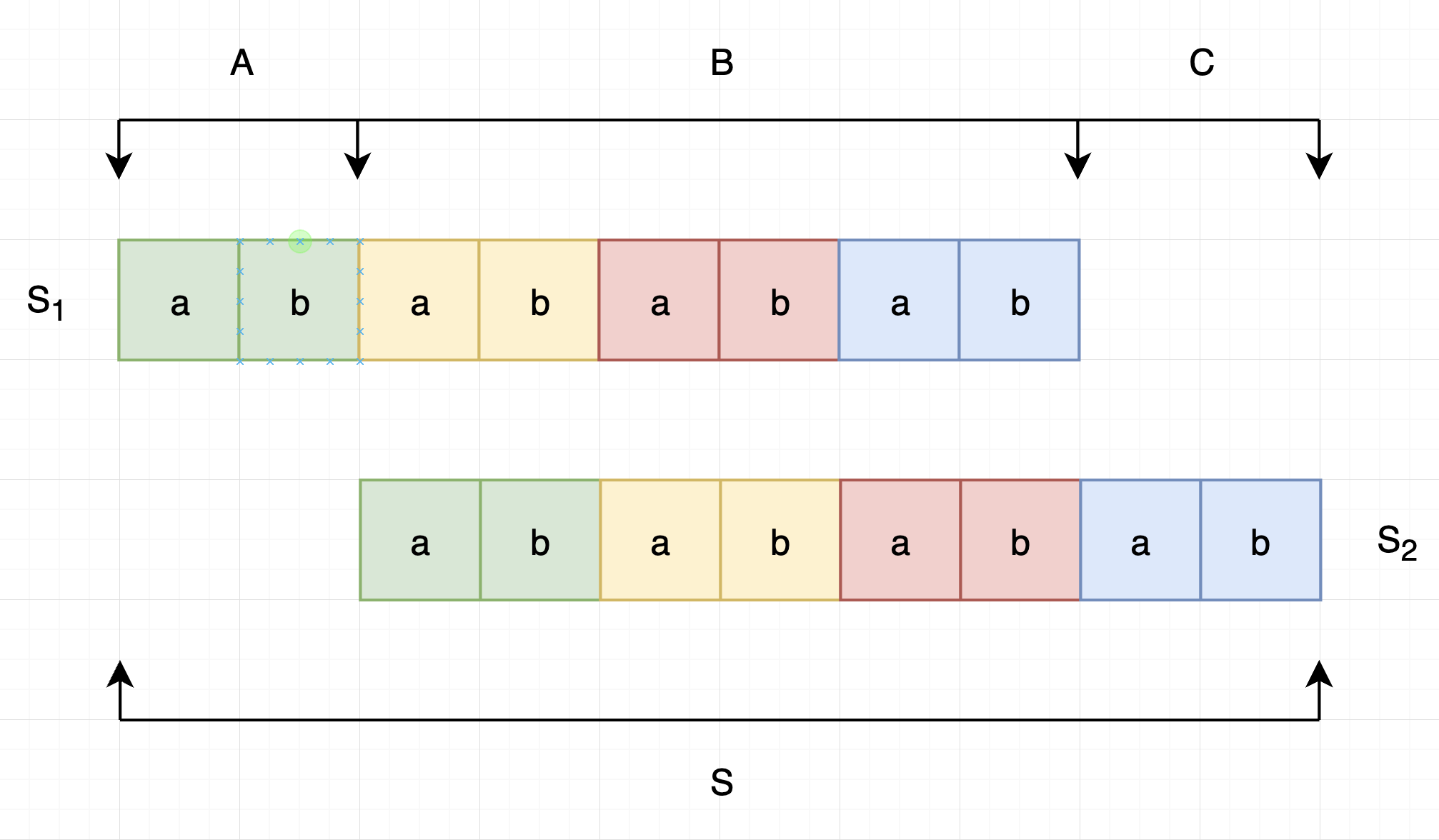
S被分为了前缀AB和后缀BC，如果AB的长度是C的整数倍，那么我们以C的长度为单位将S进行划分得到上图。因为AB和BC是相同的字符串，显然同一色块的子串是相同的；同时因为B是公用部分，上下对应色块位置的子串也是相同的。结合这两点，我们就可以证明所有色块的子串都是相同的。

---

代码实现

Java

暴力法

class Solution {
    public boolean repeatedSubstringPattern(String s) {
        int len = s.length();
        for (int i = 1; i <= len / 2; i++) {
            if (len % i == 0 && s.substring(0, i).repeat(len / i).equals(s)) {
                return true;
            }
        }
        return false;
    }
}

KMP

class Solution {
    public boolean repeatedSubstringPattern(String s) {
        int len = s.length();
        int[] next = new int[len];
        int i = 0, j = 1;
        while (j < len) {
            if (s.charAt(j) == s.charAt(i)) {
                next[j++] = ++i;
            } else if (i > 0) {
                i = next[i - 1];
            } else {
                ++j;
            }
        }
        return next[len - 1] > 0 && next[len - 1] % (len - next[len - 1]) == 0;
    }
}