一、引入
随机数据中,BST 一次操作的期望复杂度为 (mathcal{O}(log n))。
然而,BST 很容易退化,例如在 BST 中一次插入一个有序序列,将会得到一条链,平均每次操作的复杂度为 (mathcal{O}(n))。我们称这种左右子树大小相差很大的 BST 是“不平衡”的。
有很多方法可以维持 BST 的平衡,从而产生了各种平衡树。
Treap 就是常见平衡树中的一种。
二、简介
满足 BST 性质且中序遍历为相同序列的二叉查找树是不唯一的。这些二叉查找树是等价的,它们维护的是相同的一组数值。在这些二叉查找树上执行同样的操作,将得到相同的结果。
因此,我们可以在维持 BST 性质的基础上,通过改变二叉查找树的 形态,使得树上每个节点的左右子树大小达到平衡,从而使整棵树的深度维持在 (mathcal{O}(log n)) 级别。
Treap 改变形态并保持 BST 性质的方式为“旋转”,并且保持平衡而不至于退化为链。
Treap=Tree+Heap。Treap 是利用堆的性质来维护平衡的一种平衡树。对每个节点额外存储一个随机值,根据随机值调整 Treap 的形态,使其满足 BST 性质外,还满足父节点的随机值 (geq) 子节点的随机值。
三、Treap
前面说过,为了使 Treap 保持平衡而进行旋转操作。
旋转的本质是将某个节点上移一个位置。旋转需要保证 :
-
整棵树的中序遍历不变(不能破坏 BST 的性质)。
-
受影响的节点维护的信息依然正确有效。
每个节点在建立时,赋予其一个随机值,通过旋转操作使得随机值满足大根堆的性质。这样可以使得树高期望保持在 (mathcal{O}(log n)) 。
1. 旋转操作
在 Treap 中的旋转分为两种:左旋 和 右旋。
注意:某些书籍把左右旋定义为一个节点绕其父节点向左或向右旋转。而这里的 Treap 代码仅记录左右子节点,没有记录父节点,方便起见,统一以“旋转前处于父节点位置”(旋转后处于子节点位置)的节点作为左右旋的作用对象。
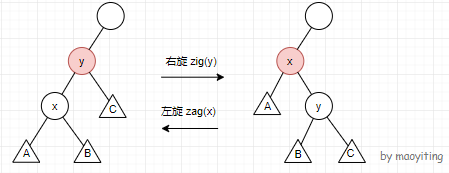
以右旋为例。如图所示,在初始情况下,(x) 是 (y) 的左子节点,(A) 和 (B) 分别是 (x) 的左右子树,(C) 是 (y) 的右子树。
“右旋”操作在保持 BST 性质的基础上,把 (x) 变为 (y) 的父节点。因为 (x) 的关键码小于 (y) 的关键码,所以 (y) 应该作为 (x) 的右子节点。
当 (x) 变成 (y) 的父节点后,(y) 的左子树就空了出来,于是 (x) 原来的右子树 (B) 就恰好作为 (y) 的左子树。
-
左旋:将右儿子提到当前节点,自己作为右儿子的左儿子,右儿子原来的左儿子变成自己新的右儿子。
-
右旋:将左儿子提到当前节点,自己作为左儿子的右儿子,左儿子原来的右儿子变成自己新的左儿子。
右旋将左儿子上移,左旋将右儿子上移。左右旋并 没有本质区别。其目的相同,即将指定节点上移一个位置。
旋转后的二叉树仍满足 BST 的性质。
void zig(int &p){ //右旋操作。zig(p) 可以理解成把 p 的左子节点绕着 p 向右旋转。 int q=lc[p]; lc[p]=rc[q],rc[q]=p,p=q; //注意 p 是引用 } void zag(int &p){ //左旋操作。zag(p) 可以理解成把 p 的右子节点绕着 p 向左旋转。 int q=rc[p]; rc[p]=lc[q],lc[q]=p,p=q; //注意 p 是引用 }
2. 随机权值
合理的旋转操作可使 BST 更“平衡”。如下图,经过一些旋转操作,这棵 BST 变得比较平衡了。

在随机数据下,普通的 BST 就是趋近平衡的。Treap 的思想就是利用“随机”来创造平衡条件。因为在旋转过程中必须维持 BST 性质,所以 Treap 就把“随机”作用在堆性质上。
具体来说,Treap 在插入每个新节点时,给该节点随机生成一个额外的权值。当某个节点不满足大根堆性质时,就执行旋转操作,使该点与其父节点的关系发生对换。
每次删除/插入时通过随机的值决定要不要旋转即可,其他操作与 BST 类似。
特别地,对于删除操作,由于 Treap 支持旋转,我们可以直接找到需要删除的节点,并把它 向下旋转成叶节点,最后直接删除。这样就避免了采取类似普通 BST 的删除方法可能导致的节点信息更新、堆性质维护等复杂问题。
Treap 通过适当的旋转操作,在 维持节点关键码满足 BST 性质的同时,还使每个节点上随机生成的额外权值满足大根堆性质。Treap 是一种平衡的二叉查找树,检索、插入、求前驱后继以及删除节点的时间复杂度都是 (mathcal{O}(log n))。
四、模板
Luogu P3369 普通平衡树
题目大意:你需要写一种数据结构,来维护一些数,其中需要提供以下操作:
- 插入数值 (x)
- 删除数值 (x)(若有多个相同的数,应只删除一个)
- 查询数值 (x) 的排名(若有多个相同的数,应输出最小的排名)
- 查询排名为 (x) 的数
- 求数值 (x) 的前驱(前驱定义为小于 (x) 的最大的数)
- 求数值 (x) 的后继(后继定义为大于 (x) 的最小的数)
(1leq n leq 10^5,|x| leq 10^7)。
Solution:平衡树模板题,用 Treap 实现即可。
数据中可能有相同的数值。记 (cnt(u)) 表示节点 (u) 对应数值的出现次数,初始时为 (1)。(这里的“对应数值”就是关键码)
若插入已经存在的数值,就直接把 (cnt) 值加 (1)。删除时,若 (cnt(u)>1),则把 (cnt(u)) 减 (1);否则删除该节点。
再记 (sz(u)) 表示以 (u) 为根的子树中所有节点的 (cnt) 之和。在插入或删除时从下往上更新 (sz) 信息。另外,在旋转操作时,也需要同时修改 (sz)。
在 BST 检索的基础上,通过判断 (sz(lc(u))) 和 (sz(rc(u))) 的大小,选择适当的一侧递归,就能查询排名了。
在插入和删除操作时,Treap 的形态会发生变化,一般使用递归实现,以便于在回溯时更新 Treap 上存储的 (sz) 等信息。
#include<bits/stdc++.h> #define int long long using namespace std; const int N=1e5+5; int n,opt,x,tot,rt,lc[N],rc[N],val[N],rnd[N],sz[N],cnt[N],ans; //rnd(u) 表示节点 u 的随机值 void upd(int p){ sz[p]=sz[lc[p]]+sz[rc[p]]+cnt[p]; } int getnew(int k){ val[++tot]=k,rnd[tot]=rand(),cnt[tot]=sz[tot]=1; return tot; } void build(){ getnew(-1e18),getnew(1e18),rt=1,rc[1]=2,upd(rt); } void rotate(int &p,int dir){ //dir= 0 右旋 1 左旋 int q=!dir?lc[p]:rc[p]; if(!dir) lc[p]=rc[q],rc[q]=p,p=q,upd(rc[p]),upd(p); else rc[p]=lc[q],lc[q]=p,p=q,upd(lc[p]),upd(p); } void insert(int &p,int k){ if(!p){p=getnew(k);return ;} if(val[p]==k){cnt[p]++,upd(p);return ;} if(k<val[p]){insert(lc[p],k);if(rnd[p]<rnd[lc[p]]) rotate(p,0);} //不满足堆性质,右旋 else{insert(rc[p],k);if(rnd[p]<rnd[rc[p]]) rotate(p,1);} //不满足堆性质,左旋 upd(p); } void del(int &p,int k){ if(!p) return ; if(val[p]==k){ //检索到 k if(cnt[p]>1){cnt[p]--,upd(p);return ;} //有重复,让 cnt 值减 1 即可 if(lc[p]||rc[p]){ //不是叶子节点,向下旋转 if(!rc[p]||rnd[lc[p]]>rnd[rc[p]]) rotate(p,0),del(rc[p],k); else rotate(p,1),del(lc[p],k); upd(p); } else p=0; return ; //叶子节点直接删除 } del(k<val[p]?lc[p]:rc[p],k),upd(p); } int rank(int p,int k){ if(!p) return 0; if(val[p]==k) return sz[lc[p]]+1; return k<val[p]?rank(lc[p],k):rank(rc[p],k)+sz[lc[p]]+cnt[p]; } int Kth(int p,int rk){ if(!p) return 1e18; if(sz[lc[p]]>=rk) return Kth(lc[p],rk); if(sz[lc[p]]+cnt[p]>=rk) return val[p]; return Kth(rc[p],rk-sz[lc[p]]-cnt[p]); } int pre(int k){ int ans=1,p=rt; while(p){ if(val[p]==k){ if(lc[p]>0){p=lc[p]; while(rc[p]>0) p=rc[p]; ans=p;} //左子树上一直向右走 break; } if(val[p]<k&&val[p]>val[ans]) ans=p; p=k<val[p]?lc[p]:rc[p]; } return val[ans]; } int nxt(int k){ int ans=2,p=rt; while(p){ if(val[p]==k){ if(rc[p]>0){p=rc[p]; while(lc[p]>0) p=lc[p]; ans=p;} //右子树上一直向左走 break; } if(val[p]>k&&val[p]<val[ans]) ans=p; p=k<val[p]?lc[p]:rc[p]; } return val[ans]; } signed main(){ scanf("%lld",&n),build(); while(n--){ scanf("%lld%lld",&opt,&x),ans=-1; if(opt==1) insert(rt,x); else if(opt==2) del(rt,x); else if(opt==3) ans=rank(rt,x)-1; else if(opt==4) ans=Kth(rt,x+1); else if(opt==5) ans=pre(x); else ans=nxt(x); if(~ans) printf("%lld ",ans); } return 0; }
少了一点压行的版本:
#include<bits/stdc++.h> #define int long long using namespace std; const int N=1e5+5; int n,opt,x,tot,rt,lc[N],rc[N],val[N],rnd[N],sz[N],cnt[N],ans; //rnd(u) 表示节点 u 的随机值 void upd(int p){ sz[p]=sz[lc[p]]+sz[rc[p]]+cnt[p]; } int getnew(int k){ val[++tot]=k,rnd[tot]=rand(),cnt[tot]=sz[tot]=1; return tot; } void build(){ getnew(-1e18),getnew(1e18),rt=1,rc[1]=2,upd(rt); } void zig(int &p){ //右旋 int q=lc[p]; lc[p]=rc[q],rc[q]=p,p=q,upd(rc[p]),upd(p); } void zag(int &p){ //左旋 int q=rc[p]; rc[p]=lc[q],lc[q]=p,p=q,upd(lc[p]),upd(p); } void insert(int &p,int k){ if(!p){p=getnew(k);return ;} if(val[p]==k){cnt[p]++,upd(p);return ;} if(k<val[p]){ insert(lc[p],k); if(rnd[p]<rnd[lc[p]]) zig(p); //不满足堆性质,右旋 } else{ insert(rc[p],k); if(rnd[p]<rnd[rc[p]]) zag(p); //不满足堆性质,左旋 } upd(p); } void del(int &p,int k){ if(!p) return ; if(val[p]==k){ //检索到 k if(cnt[p]>1){cnt[p]--,upd(p);return ;} //有重复,让 cnt 值减 1 即可 if(lc[p]||rc[p]){ //不是叶子节点,向下旋转 if(!rc[p]||rnd[lc[p]]>rnd[rc[p]]) zig(p),del(rc[p],k); else zag(p),del(lc[p],k); upd(p); } else p=0; return ; //叶子节点直接删除 } del(k<val[p]?lc[p]:rc[p],k),upd(p); } int rank(int p,int k){ if(!p) return 0; if(val[p]==k) return sz[lc[p]]+1; if(k<val[p]) return rank(lc[p],k); return rank(rc[p],k)+sz[lc[p]]+cnt[p]; } int Kth(int p,int rk){ if(!p) return 1e18; if(sz[lc[p]]>=rk) return Kth(lc[p],rk); if(sz[lc[p]]+cnt[p]>=rk) return val[p]; return Kth(rc[p],rk-sz[lc[p]]-cnt[p]); } int pre(int k){ int ans=1,p=rt; while(p){ if(val[p]==k){ if(!(p=lc[p])) break; while(rc[p]>0) p=rc[p]; //左子树上一直向右走 ans=p;break; } if(val[p]<k&&val[p]>val[ans]) ans=p; p=k<val[p]?lc[p]:rc[p]; } return val[ans]; } int nxt(int k){ int ans=2,p=rt; while(p){ if(val[p]==k){ if(!(p=rc[p])) break; while(lc[p]>0) p=lc[p]; //右子树上一直向左走 ans=p;break; } if(val[p]>k&&val[p]<val[ans]) ans=p; p=k<val[p]?lc[p]:rc[p]; } return val[ans]; } signed main(){ scanf("%lld",&n),build(); while(n--){ scanf("%lld%lld",&opt,&x),ans=-1; if(opt==1) insert(rt,x); else if(opt==2) del(rt,x); else if(opt==3) ans=rank(rt,x)-1; else if(opt==4) ans=Kth(rt,x+1); else if(opt==5) ans=pre(x); else ans=nxt(x); if(~ans) printf("%lld ",ans); } return 0; }
注:rank(rt,x)-1 和 Kth(rt,x+1) 的加减一是因为初始时额外插入了关键码为 (+infty) 和 (−infty) 的节点。
五、参考资料
- 《算法竞赛进阶指南》(大棒子)