AtCoder Grand Contest 019 F-yes or no
解题思路:
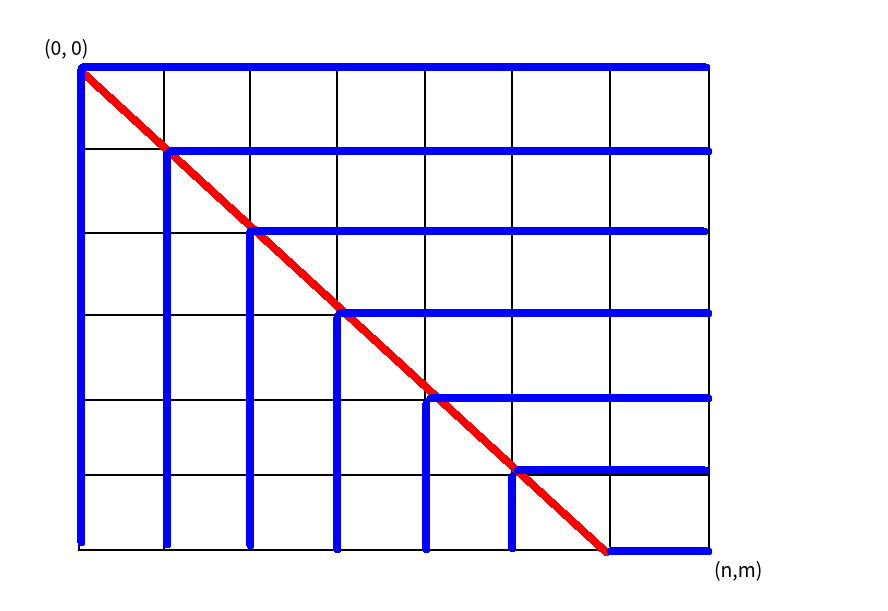
考虑一个贪心策略,假设当前还有 (x) 道 ( ext{yes}) 和 (y) 道 ( ext{no}) ,那么一定猜较大者,如果 (x=y) 就相当于随便猜一个,把 ((x, y)) 用坐标表示,把所有在这种决策下猜对的边用蓝色表示,走过这样一条边就相当于有 (1) 的贡献,然后会发现从 ((0,0)) 到 ((n,m)) 的所有路径经过的蓝色的边的数量都是相同的 (max(n,m)) 条,也就是说只需要考虑每次在 ((x=y)) 时的决策的贡献之和就好了。
这个东西就是经过这个点的路径方案数乘上 (dfrac{1}{2}) ,组合数搞搞就好了
code
/*program by mangoyang*/
#pragma GCC optimize("Ofast", "inline")
#include <bits/stdc++.h>
#define inf (0x7f7f7f7f)
#define Max(a, b) ((a) > (b) ? (a) : (b))
#define Min(a, b) ((a) < (b) ? (a) : (b))
typedef long long ll;
using namespace std;
template <class T>
inline void read(T &x){
int f = 0, ch = 0; x = 0;
for(; !isdigit(ch); ch = getchar()) if(ch == '-') f = 1;
for(; isdigit(ch); ch = getchar()) x = x * 10 + ch - 48;
if(f) x = -x;
}
const int N = 1000005, mod = 998244353;
ll js[1000005], inv[1000005], n, m, ans;
inline ll Pow(ll a, ll b){
ll ans = 1;
for(; b; b >>= 1, a = a * a % mod)
if(b & 1) ans = ans * a % mod;
return ans;
}
inline ll C(ll x, ll y){ return js[x] * inv[y] % mod * inv[x-y] % mod; }
int main(){
read(n), read(m);
if(n > m) swap(n, m);
js[0] = inv[0] = 1;
for(int i = 1; i < N; i++)
js[i] = 1ll * js[i-1] * i % mod, inv[i] = Pow(js[i], mod - 2);
for(int i = 1; i <= n; i++)
(ans += C(n + m - 2 * i, m - i) * C(2 * i, i) % mod) %= mod;
cout << ((m + ans * inv[2] % mod * Pow(C(n + m, n), mod - 2) % mod) % mod + mod) % mod << endl;
}