Canny算子是John Canny在1986年提出的,那年老大爷才28岁,该文章发表在PAMI顶级期刊上的(1986. A computational approach to edge detection. IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 8, 1986, pp. 679-698)。老大爷目前在加州伯克利做machine learning,80-90年代视觉都是图像处理,现在做视觉都是机器学习的天下,大爷的主页(http://www.cs.berkeley.edu/~jfc/)。
Canny算子与Marr(LoG)边缘检测方法类似(Marr大爷号称计算机视觉之父),也属于是先平滑后求导数的方法。John Canny研究了最优边缘检测方法所需的特性,给出了评价边缘检测性能优劣的三个指标:
1 好的信噪比,即将非边缘点判定为边缘点的概率要低,将边缘点判为非边缘点的概率要低;
2 高的定位性能,即检测出的边缘点要尽可能在实际边缘的中心;
3 对单一边缘仅有唯一响应,即单个边缘产生多个响应的概率要低,并且虚假响应边缘应该得到最大抑制。
用一句话说,就是希望在提高对景物边缘的敏感性的同时,可以抑制噪声的方法才是好的边缘提取方法。
Canny算子求边缘点具体算法步骤如下:
1. 用高斯滤波器平滑图像.
2. 用一阶偏导有限差分计算梯度幅值和方向
3. 对梯度幅值进行非极大值抑制
4. 用双阈值算法检测和连接边缘.
具体的步骤是能容易理解,现在就是用C语言怎么实现了,在参考了网上诸多教程的基础下,写了个代码给大家参考,肯定有不少问题,希望能得到大家的指点。
首先用白话叙述下Canny算子的原理:看作者写的paper题目就是边缘检测,何为边缘?图象局部区域亮度变化显著的部分,对于灰度图像来说,也就是灰度值有一个明显变化,既从一个灰度值在很小的缓冲区域内急剧变化到另一个灰度相差较大的灰度值。依据我仅有的数学知识,怎么表征这种灰度值的变化呢?导数就是表征变化率的,但是数字图像都是离散的,也就是导数肯定会用差分来代替。也就是具体算法中的步骤2。但是在真实的图像中,一般会有噪声,噪声会影响梯度(换不严格说法 偏导数)的计算,所以步骤1上来先滤波。理论上将图像梯度幅值的元素值越大,说明图像中该点的梯度值越大,但这不能说明该点就是边缘。在Canny算法中,非极大值抑制(步骤3)是进行边缘检测的重要步骤,通俗意义上是指寻找像素点局部最大值,沿着梯度方向,比较它前面和后面的梯度值进行了。步骤4,是一个典型算法,有时候我们并不像一刀切,也就是超过阈值的都是边缘点,而是设为两个阈值,希望在高阈值和低阈值之间的点也可能是边缘点,而且这些点最好在高阈值的附近,也就是说这些中间阈值的点是高阈值边缘点的一种延伸。所以步骤4用了双阈值来检测和连接边缘。
基本原理简单说完,上代码,代码按照下面6步骤叙述。
第一步:灰度化
第二步:高斯滤波
第三步:计算梯度值和方向
第四步:非极大值抑制
第五步:双阈值的选取
第六步:边缘检测
1 把彩色图像变成灰度图像。该部分主要是为像我这样的小菜鸟准备的。
该部分是按照Canny算法通常处理的图像为灰度图,如果获取的彩色图像,那首先就得进行灰度化。以RGB格式的彩图为例,通常灰度化采用的公式是:
Gray=0.299R+0.587G+0.114B;
说个我经常出问题的代码:OpenCvGrayImage->imageData[i*OpenCvGrayImage->widthStep+j] 这是opencv iplimage格式通过直接访问内存读取像素值的方式,我一直搞不清楚,i*widthStep还是j*widthStep。
记住一点,是高*widthStep就行。而且是*widthStep,而不是乘以width.如果图像的宽度不是4的倍数,opencv貌似还有补齐这一说法,所以mark一下。
代码如下:

1 ////////第一步:灰度化 2 IplImage * ColorImage=cvLoadImage("c:\photo.bmp",1); 3 if (ColorImage==NULL) 4 { 5 printf("image read error"); 6 return 0; 7 } 8 cvNamedWindow("Sourceimg",0); 9 cvShowImage("Sourceimg",ColorImage); // 10 IplImage * OpenCvGrayImage; 11 OpenCvGrayImage=cvCreateImage(cvGetSize(ColorImage),ColorImage->depth,1); 12 float data1,data2,data3; 13 for (int i=0;i<ColorImage->height;i++) 14 { 15 for (int j=0;j<ColorImage->width;j++) 16 { 17 data1=(uchar)(ColorImage->imageData[i*ColorImage->widthStep+j*3+0]); 18 data2=(uchar)(ColorImage->imageData[i*ColorImage->widthStep+j*3+1]); 19 data3=(uchar)(ColorImage->imageData[i*ColorImage->widthStep+j*3+2]); 20 OpenCvGrayImage->imageData[i*OpenCvGrayImage->widthStep+j]=(uchar)(0.07*data1 + 0.71*data2 + 0.21*data3); 21 } 22 } 23 cvNamedWindow("GrayImage",0); 24 cvShowImage("GrayImage",OpenCvGrayImage); //显示灰度图 25 cvWaitKey(0); 26 cvDestroyWindow("GrayImage");
2 对图像高斯滤波,图像高斯滤波的实现可以用两个一维高斯核分别两次加权实现,也就是先一维X方向卷积,得到的结果再一维Y方向卷积。当然也可以直接通过一个二维高斯核一次卷积实现。也就是二维卷积模板,由于水平有限,只说二维卷积模板怎么算。
首先,一维高斯函数:
二维高斯函数:
是不是和一维很像,其实就是两个一维乘积就是二维,有的书和文章中将r2=x2+y2 来表示距离的平方,也就是当前要卷积的点离核心的距离的平方,如果是3*3的卷积模板,核心就是中间的那个元素,那左上角的点到核心的距离是多少呢,就是sqrt(1+1)=sqrt(2),距离的平方 r2=2。基于这个理论,那么模板中每一个点的高斯系数可以由上面的公式计算,这样得到的是不是最终的模板呢?答案不是,需要归一化,也即是每一个点的系数要除以所有系数之和,这样才是最终的二维高斯模板。
这个里面有个小知识点,要想计算上面的系数,需要知道高斯函数的标准差σ (sigma),还需要知道选3*3还是5*5的模板,也就是模板要多大,实际应用的时候,这两者是有关系的,根据数理统计的知识,高斯分布的特点就是数值分布在(μ—3σ,μ+3σ)中的概率为0.9974,也就是模板的大小其实就是6σ这么大就OK了,但是6σ可能不是奇数,因为我们一定要保证有核心。所以模板窗口的大小一般采用1+2*ceil(3*nSigma) ceil是向上取整函数,例如ceil(0.6)=1。
计算得到模板,那就是直接卷积就OK,卷积的意思就是图像中的点附近的模板大小区域乘以高斯模板区域,得到的结果就是该点卷积后的结果。卷积的核心意义就是获取原始图像中像模板特征的性质。插一句话,目前深度学习中很火的一个卷积神经网络CNN,就是利用卷积的原理,通过学习出这些卷积模板来识别检测。
代码如下:

////////第二步:高斯滤波 /////// double nSigma=0.2; int nWindowSize=1+2*ceil(3*nSigma);//通过sigma得到窗口大小 int nCenter=nWindowSize/2; int nWidth=OpenCvGrayImage->width; int nHeight=OpenCvGrayImage->height; IplImage * pCanny; pCanny=cvCreateImage(cvGetSize(ColorImage),ColorImage->depth,1); //生成二维滤波核 double *pKernel_2=new double[nWindowSize*nWindowSize]; double d_sum=0.0; for(int i=0;i<nWindowSize;i++) { for (int j=0;j<nWindowSize;j++) { double n_Disx=i-nCenter;//水平方向距离中心像素距离 double n_Disy=j-nCenter; pKernel_2[j*nWindowSize+i]=exp(-0.5*(n_Disx*n_Disx+n_Disy*n_Disy)/(nSigma*nSigma))/(2.0*3.1415926)*nSigma*nSigma; d_sum=d_sum+pKernel_2[j*nWindowSize+i]; } } for(int i=0;i<nWindowSize;i++)//归一化处理 { for (int j=0;j<nWindowSize;j++) { pKernel_2[j*nWindowSize+i]=pKernel_2[j*nWindowSize+i]/d_sum; } } //输出模板 for (int i=0;i<nWindowSize*nWindowSize;i++) { if (i%(nWindowSize)==0) { printf(" "); } printf("%.10f ",pKernel_2[i]); } //滤波处理 for (int s=0;s<nWidth;s++) { for (int t=0;t<nHeight;t++) { double dFilter=0; double dSum=0; //当前坐标(s,t) //获取8邻域 for (int x=-nCenter;x<=nCenter;x++) { for (int y=-nCenter;y<=nCenter;y++) { if ((x+s>=0)&&(x+s<nWidth)&&(y+t>=0)&&(y+t<nHeight))//判断是否越界 { double currentvalue=(double)OpenCvGrayImage->imageData[(y+t)*OpenCvGrayImage->widthStep+x+s]; dFilter+=currentvalue*pKernel_2[x+nCenter+(y+nCenter)*nCenter]; dSum+=pKernel_2[x+nCenter+(y+nCenter)*nCenter]; } } } pCanny->imageData[t*pCanny->widthStep+s]=(uchar)(dFilter/dSum); } } cvNamedWindow("GaussImage",0); cvShowImage("GaussImage",pCanny); //显示高斯图 cvWaitKey(0); cvDestroyWindow("GaussImage");
3 计算梯度值和方向,图像灰度值的梯度一般使用一阶有限差分来进行近似,这样就可以得图像在x和y方向上偏导数的两个矩阵。本文采用非常简单的算子,当然你也可以选择高大上的算子或者自己写的:
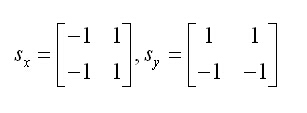

其中f为图像灰度值,P代表X方向梯度幅值,Q代表Y方向 梯度幅值,M是该点幅值,Θ是梯度方向,也就是角度。
代码如下:

1 ////////////////////////////////////////////////////////// 2 ////////第三步:计算梯度值和方向 3 //////////////////同样可以用不同的检测器////////////////加上把图像放到0-255之间////// 4 ///// P[i,j]=(S[i+1,j]-S[i,j]+S[i+1,j+1]-S[i,j+1])/2 ///// 5 ///// Q[i,j]=(S[i,j]-S[i,j+1]+S[i+1,j]-S[i+1,j+1])/2 ///// 6 ///////////////////////////////////////////////////////////////// 7 double *P=new double[nWidth*nHeight]; 8 double *Q=new double[nWidth*nHeight]; 9 int *M=new int[nWidth*nHeight]; 10 //IplImage * M;//梯度结果 11 //M=cvCreateImage(cvGetSize(ColorImage),ColorImage->depth,1); 12 double *Theta=new double[nWidth*nHeight]; 13 int nwidthstep=pCanny->widthStep; 14 for(int iw=0;iw<nWidth-1;iw++) 15 { 16 for (int jh=0;jh<nHeight-1;jh++) 17 { 18 P[jh*nWidth+iw]=(double)(pCanny->imageData[min(iw+1,nWidth-1)+jh*nwidthstep]-pCanny->imageData[iw+jh*nwidthstep]+ 19 pCanny->imageData[min(iw+1,nWidth-1)+min(jh+1,nHeight-1)*nwidthstep]-pCanny->imageData[iw+min(jh+1,nHeight-1)*nwidthstep])/2; 20 Q[jh*nWidth+iw]=(double)(pCanny->imageData[iw+jh*nwidthstep]-pCanny->imageData[iw+min(jh+1,nHeight-1)*nwidthstep]+ 21 pCanny->imageData[min(iw+1,nWidth-1)+jh*nwidthstep]-pCanny->imageData[min(iw+1,nWidth-1)+min(jh+1,nHeight-1)*nwidthstep])/2; 22 } 23 } 24 //计算幅值和方向 25 for(int iw=0;iw<nWidth-1;iw++) 26 { 27 for (int jh=0;jh<nHeight-1;jh++) 28 { 29 M[jh*nWidth+iw]=(int)sqrt(P[jh*nWidth+iw]*P[jh*nWidth+iw]+Q[jh*nWidth+iw]*Q[jh*nWidth+iw]+0.5); 30 Theta[jh*nWidth+iw]=atan2(Q[jh*nWidth+iw],P[jh*nWidth+iw])*180/3.1415; 31 if (Theta[jh*nWidth+iw]<0) 32 { 33 Theta[jh*nWidth+iw]=360+Theta[jh*nWidth+iw]; 34 } 35 } 36 }
4 非极大值抑制是进行边缘检测的一个重要步骤,通俗意义上是指寻找像素点局部最大值。沿着梯度方向,比较它前面和后面的梯度值进行了。见下图。
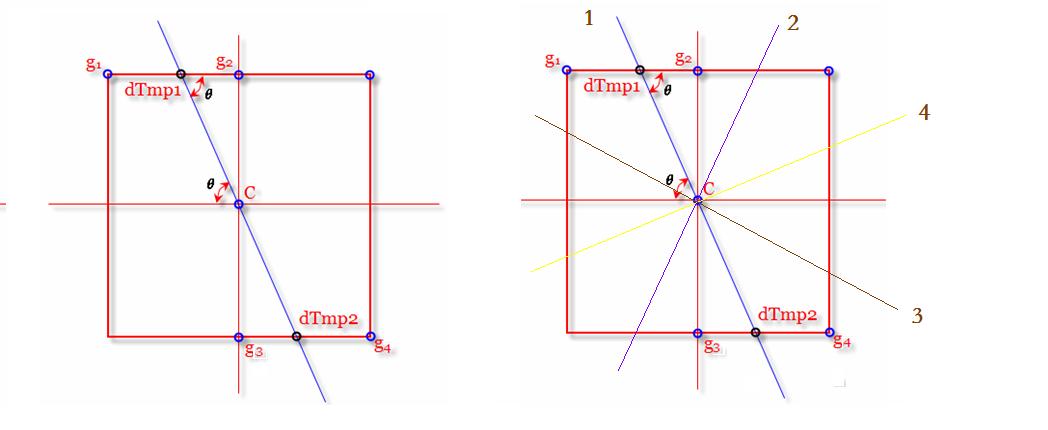
上图中左右图:g1、g2、g3、g4都代表像素点,很明显它们是c的八领域中的4个,左图中c点是我们需要判断的点,蓝色的直线是它的梯度方向,也就是说c要是局部极大值,它的梯度幅值M需要大于直线与g1g2和g2g3的交点,dtmp1和dtmp2处的梯度幅值。但是dtmp1和dtmp2不是整像素,而是亚像素,也就是坐标是浮点的,那怎么求它们的梯度幅值呢?线性插值,例如dtmp1在g1、g2之间,g1、g2的幅值都知道,我们只要知道dtmp1在g1、g2之间的比例,就能得到它的梯度幅值,而比例是可以靠夹角计算出来的,夹角又是梯度的方向。
写个线性插值的公式:设g1的幅值M(g1),g2的幅值M(g2),则dtmp1可以很得到:
M(dtmp1)=w*M(g2)+(1-w)*M(g1)
其中w=distance(dtmp1,g2)/distance(g1,g2)
distance(g1,g2) 表示两点之间的距离。实际上w是一个比例系数,这个比例系数可以通过梯度方向(幅角的正切和余切)得到。
右边图中的4个直线就是4个不同的情况,情况不同,g1、g2、g3、g4代表c的八领域中的4个坐标会有所差异,但是线性插值的原理都是一致的。
代码如下:

1 ////////第四步:非极大值抑制 2 //注意事项 权重的选取,也就是离得近权重大 3 ///////////////////////////////////////////////////////////////// 4 IplImage * N;//非极大值抑制结果 5 N=cvCreateImage(cvGetSize(ColorImage),ColorImage->depth,1); 6 IplImage * OpencvCannyimg;//非极大值抑制结果 7 OpencvCannyimg=cvCreateImage(cvGetSize(ColorImage),ColorImage->depth,1); 8 int g1=0, g2=0, g3=0, g4=0; //用于进行插值,得到亚像素点坐标值 9 double dTmp1=0.0, dTmp2=0.0; //保存两个亚像素点插值得到的灰度数据 10 double dWeight=0.0; //插值的权重 11 12 for(int i=1;i<nWidth-1;i++) 13 { 14 for(int j=1;j<nHeight-1;j++) 15 { 16 //如果当前点梯度为0,该点就不是边缘点 17 if (M[i+j*nWidth]==0) 18 { 19 N->imageData[i+j*nwidthstep]=0; 20 }else 21 { 22 ////////首先判断属于那种情况,然后根据情况插值/////// 23 ////////////////////第一种情况/////////////////////// 24 ///////// g1 g2 ///////////// 25 ///////// C ///////////// 26 ///////// g3 g4 ///////////// 27 ///////////////////////////////////////////////////// 28 if((Theta[i+j*nWidth]>=90&&Theta[i+j*nWidth]<135)||(Theta[i+j*nWidth]>=270&&Theta[i+j*nWidth]<315)) 29 { 30 g1=M[i-1+(j-1)*nWidth]; 31 g2=M[i+(j-1)*nWidth]; 32 g3=M[i+(j+1)*nWidth]; 33 g4=M[i+1+(j+1)*nWidth]; 34 dWeight=fabs(P[i+j*nWidth])/fabs(Q[i+j*nWidth]); 35 dTmp1=g1*dWeight+(1-dWeight)*g2; 36 dTmp2=g4*dWeight+(1-dWeight)*g3; 37 ////////////////////第二种情况/////////////////////// 38 ///////// g1 ///////////// 39 ///////// g2 C g3 ///////////// 40 ///////// g4 ///////////// 41 ///////////////////////////////////////////////////// 42 }else if((Theta[i+j*nWidth]>=135&&Theta[i+j*nWidth]<180)||(Theta[i+j*nWidth]>=315&&Theta[i+j*nWidth]<360)) 43 { 44 g1=M[i-1+(j-1)*nWidth]; 45 g2=M[i-1+(j)*nWidth]; 46 g3=M[i+1+(j)*nWidth]; 47 g4=M[i+1+(j+1)*nWidth]; 48 dWeight=fabs(Q[i+j*nWidth])/fabs(P[i+j*nWidth]); 49 dTmp1=g1*dWeight+(1-dWeight)*g2; 50 dTmp2=g4*dWeight+(1-dWeight)*g3; 51 ////////////////////第三种情况/////////////////////// 52 ///////// g1 g2 ///////////// 53 ///////// C ///////////// 54 ///////// g4 g3 ///////////// 55 ///////////////////////////////////////////////////// 56 }else if((Theta[i+j*nWidth]>=45&&Theta[i+j*nWidth]<90)||(Theta[i+j*nWidth]>=225&&Theta[i+j*nWidth]<270)) 57 { 58 g1=M[i+1+(j-1)*nWidth]; 59 g2=M[i+(j-1)*nWidth]; 60 g3=M[i+(j+1)*nWidth]; 61 g4=M[i-1+(j+1)*nWidth]; 62 dWeight=fabs(P[i+j*nWidth])/fabs(Q[i+j*nWidth]); 63 dTmp1=g1*dWeight+(1-dWeight)*g2; 64 dTmp2=g4*dWeight+(1-dWeight)*g3; 65 ////////////////////第四种情况/////////////////////// 66 ///////// g1 ///////////// 67 ///////// g4 C g2 ///////////// 68 ///////// g3 ///////////// 69 ///////////////////////////////////////////////////// 70 }else if((Theta[i+j*nWidth]>=0&&Theta[i+j*nWidth]<45)||(Theta[i+j*nWidth]>=180&&Theta[i+j*nWidth]<225)) 71 { 72 g1=M[i+1+(j-1)*nWidth]; 73 g2=M[i+1+(j)*nWidth]; 74 g3=M[i-1+(j)*nWidth]; 75 g4=M[i-1+(j+1)*nWidth]; 76 dWeight=fabs(Q[i+j*nWidth])/fabs(P[i+j*nWidth]); 77 dTmp1=g1*dWeight+(1-dWeight)*g2; 78 dTmp2=g4*dWeight+(1-dWeight)*g3; 79 80 } 81 82 } 83 84 if ((M[i+j*nWidth]>=dTmp1)&&(M[i+j*nWidth]>=dTmp2)) 85 { 86 N->imageData[i+j*nwidthstep]=200; 87 88 }else N->imageData[i+j*nwidthstep]=0; 89 90 } 91 } 92 93 94 //cvNamedWindow("Limteimg",0); 95 //cvShowImage("Limteimg",N); //显示非抑制 96 //cvWaitKey(0); 97 //cvDestroyWindow("Limteimg");
5 双阈值的选取。
双阈值的选取是按照直方图来选择的,首先把梯度幅值的直方图(扯点题外话:梯度的幅值直方图和角度直方图也是SIFT算子中的一个环节)求出来,选取占直方图总数%多少(自己定,代码中定义70%)所对应的梯度幅值为高阈值,高阈值的一半为低阈值,这只是一种简单策略。也可以采用其他的。
代码如下:

1 ///////第五步:双阈值的选取 2 //注意事项 注意是梯度幅值的阈值 3 ///////////////////////////////////////////////////////////////// 4 int nHist[1024];//直方图 5 int nEdgeNum;//所有边缘点的数目 6 int nMaxMag=0;//最大梯度的幅值 7 for(int k=0;k<1024;k++) 8 { 9 nHist[k]=0; 10 } 11 for (int wx=0;wx<nWidth;wx++) 12 { 13 for (int hy=0;hy<nHeight;hy++) 14 { 15 if((uchar)N->imageData[wx+hy*N->widthStep]==200) 16 { 17 int Mindex=M[wx+hy*nWidth]; 18 nHist[M[wx+hy*nWidth]]++;//获取了梯度直方图 19 20 } 21 } 22 } 23 nEdgeNum=0; 24 for (int index=1;index<1024;index++) 25 { 26 if (nHist[index]!=0) 27 { 28 nMaxMag=index; 29 } 30 nEdgeNum+=nHist[index];//经过non-maximum suppression后有多少边缘点像素 31 } 32 //计算两个阈值 注意是梯度的阈值 33 int nThrHigh; 34 int nThrLow; 35 double dRateHigh=0.7; 36 double dRateLow=0.5; 37 int nHightcount=(int)(dRateHigh*nEdgeNum+0.5); 38 int count=1; 39 nEdgeNum=nHist[1]; 40 while((nEdgeNum<=nHightcount)&&(count<nMaxMag-1)) 41 { 42 count++; 43 nEdgeNum+=nHist[count]; 44 } 45 nThrHigh=count; 46 nThrLow= (int)(nThrHigh*dRateLow+0.5); 47 printf(" 直方图的长度 %d ",nMaxMag); 48 printf(" 梯度的阈值幅值大 %d 小阈值 %d ",nThrHigh,nThrLow);
6 边缘检测,也即是根据步骤5得到的双阈值进行连接。
首先判断该点是否超过高阈值,然后判断该点的8邻域点中寻找满足超过低阈值的点,再根据此点收集新的边缘,直到整个图像边缘闭合。整个图像找完后,将非边缘点剔除,即灰度值置0.
代码如下:

1 ////////////////////////////////////////////////////////// 2 ////////第六步:边缘检测 3 ///////////////////////////////////////////////////////////////// 4 5 for(int is=1;is<nWidth-1;is++) 6 { 7 for (int jt=1;jt<nHeight-1;jt++) 8 { 9 //CvScalar s=cvGet2D(N,jt,is); 10 //int currentvalue=s.val[0]; 11 int currentvalue=(uchar)(N->imageData[is+jt*N->widthStep]); 12 if ((currentvalue==200)&&(M[is+jt*nWidth]>=nThrHigh)) 13 //是非最大抑制后的点且 梯度幅值要大于高阈值 14 { 15 N->imageData[is+jt*nwidthstep]=255; 16 //邻域点判断 17 TraceEdge(is, jt, nThrLow, N, M); 18 } 19 } 20 } 21 for (int si=1;si<nWidth-1;si++) 22 { 23 for (int tj=1;tj<nHeight-1;tj++) 24 { 25 if ((uchar)N->imageData[si+tj*nwidthstep]!=255) 26 { 27 N->imageData[si+tj*nwidthstep]=0; 28 } 29 } 30 31 } 32 33 cvNamedWindow("Cannyimg",0); 34 cvShowImage("Cannyimg",N);
其中,邻域跟踪算法给出了两个,一种是递归,一种是非递归。
递归算法。解决了堆栈溢出问题。之前找了很多canny代码参考,其中有一个版本流传很广,但是对于大图像堆栈溢出。

1 int TraceEdge(int w, int h, int nThrLow, IplImage* pResult, int *pMag) 2 { 3 int n,m; 4 char flag = 0; 5 int currentvalue=(uchar)pResult->imageData[w+h*pResult->widthStep]; 6 if ( currentvalue== 0) 7 { 8 pResult->imageData[w+h*pResult->widthStep]= 255; 9 flag=0; 10 for (n= -1; n<=1; n++) 11 { 12 for(m= -1; m<=1; m++) 13 { 14 if (n==0 && m==0) continue; 15 int curgrayvalue=(uchar)pResult->imageData[w+n+(h+m)*pResult->widthStep]; 16 int curgrdvalue=pMag[w+n+(h+m)*pResult->width]; 17 if (curgrayvalue==200&&curgrdvalue>nThrLow) 18 if (TraceEdge(w+n, h+m, nThrLow, pResult, pMag)) 19 { 20 flag=1; 21 break; 22 } 23 } 24 if (flag) break; 25 } 26 return(1); 27 } 28 return(0); 29 }
非递归算法。如下:

1 void TraceEdge(int w, int h, int nThrLow, IplImage* pResult, int *pMag) 2 { 3 //对8邻域像素进行查询 4 int xNum[8] = {1,1,0,-1,-1,-1,0,1}; 5 int yNum[8] = {0,1,1,1,0,-1,-1,-1}; 6 int xx=0; 7 int yy=0; 8 bool change=true; 9 while(change) 10 { 11 change=false; 12 for(int k=0;k<8;k++) 13 { 14 xx=w+xNum[k]; 15 yy=h+yNum[k]; 16 // 如果该象素为可能的边界点,又没有处理过 17 // 并且梯度大于阈值 18 int curgrayvalue=(uchar)pResult->imageData[xx+yy*pResult->widthStep]; 19 int curgrdvalue=pMag[xx+yy*pResult->width]; 20 if(curgrayvalue==200&&curgrdvalue>nThrLow) 21 { 22 change=true; 23 // 把该点设置成为边界点 24 pResult->imageData[xx+yy*pResult->widthStep]=255; 25 h=yy; 26 w=xx; 27 break; 28 } 29 } 30 } 31 }
到此,整个算法写完了。打击下信心,整个算法跑起来没问题,但是没有opencv 的cvCanny 一个函数效果好。分析了下原因,一个是梯度算子选的太简单,opencv一般选用的是3*3 sobel。二是边缘连接性还是不够好,出现了很多断的,也就是邻域跟踪算法不够好。希望有高手能改进。
附上代码:http://www.pudn.com/downloads726/sourcecode/graph/detail2903773.html
整篇博客参考过网上很多canny算法的总结,在此谢过!
