本节为JVM垃圾收集的基础理论,一个GC过程在逻辑上需要经过两个步骤,即先判断哪些对象是存活的、哪些对象是死亡的,然后对死亡的对象进行回收。
一、关于回收目标
在前面我们已经了解到,JVM的内存模型划分为多个区域,由于不同区域的实现机制以及功能不同,那么各自的回收目标也不同。一般来说,内存回收主要涉及以下三个区域:
- 虚拟机栈/本地方法栈:顾名思义,该部分内存以栈的形式作为实现,那么在进栈、出栈的时候内存会自动释放,类似于C的“自动变量区域内存”;
- 堆:内存回收主要目标,可以认为类似于C中的“动态内存分配区域”,只不过C通过malloc与free函数手动进行管理,而java通过GC进行自动管理;
- 方法区:该区域回收效果很弱,虚拟机规范强制要求在这里进行回收。回收目标是常量池的回收和对类型的卸载;
二、方法区回收
方法区的回收目标是回收常量池中的废弃常量与类卸载。
2.1.常量回收
若常量池中的某常量没有任何地方引用或者使用,包括该常量不以字面量的形式被使用或引用,则可以被回收。
2.2.类卸载
满足以下条件的类可以被卸载:
- 该类所有实例已被回收;
- 该类的ClassLoader已被回收;
- 该类的类型信息,即java.lang.Class没有任何地方引用(一般为反射使用);
可以看出,对于类的卸载,要求很苛刻。因此在大量使用反射、动态代理、CGLib等字节码框架、动态生成jsp以及OSGI这类频繁自定义ClassLoader功能的场景中,都要求JVM具备类卸载功能,以保证永久带不溢出。
三、堆回收
3.1.对象存活判定
关于堆中的对象存活判定,以标记为基础,并配合其他步骤完成。
3.1.1.标记算法
(1)引用计数法
即给对象添加一个引用计数器,每有一个地方进行引用,则计数器加1。当计数器为0的时候,表示该对象可回收。
引用计数法未被JVM采用,原因是其无法解决对象间循环引用的问题,如下图所示,当堆内的两个对象循环引用,就算他们已经没用了,也无法进行回收:

(2)可达性分析算法
该算法的思想是将一系列被称为“GC ROOTS”的对象作为起点(或称根节点),向下搜索,所走过的路径称为“引用链(reference chain)”。若一个对象没有可以到达GC ROOTS的路径,则称“该对象不可达”。对于不可达对象,会被标记为回收状态。
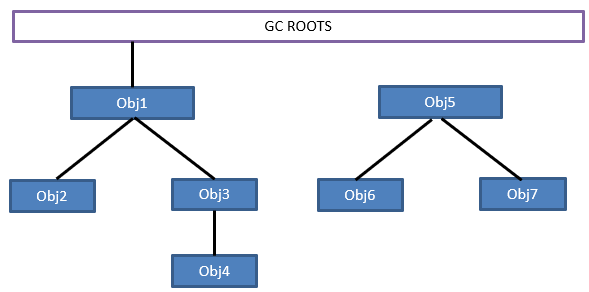
上图中,顺着GC ROOTS,Obj1、Obj2、Obj3和Obj4都是可以到达的,因此他们为存活对象;而Obj5不可到达,Obj6、Obj7即使存在指向它们的引用,但因无法到达GC ROOTS,因此为需要回收的对象。
在可达性分析算法中,最重要的就是GC ROOTS。其本质是对象,但并非所有对象都有资格作为GC ROOTS,只有以下位置的才可以:
- 栈上引用:虚拟机栈的栈帧中本地变量表内引用的对象;
- 栈上引用:本地方法栈中JNI引用的对象;
- 方法区:类静态属性引用的对象;
- 方法区:类常量引用的对象;
3.1.2.死亡判定
对象在经过标记之后,并不会马上被回收,还要经过以下一系列阶段才最终确定需要被回收:
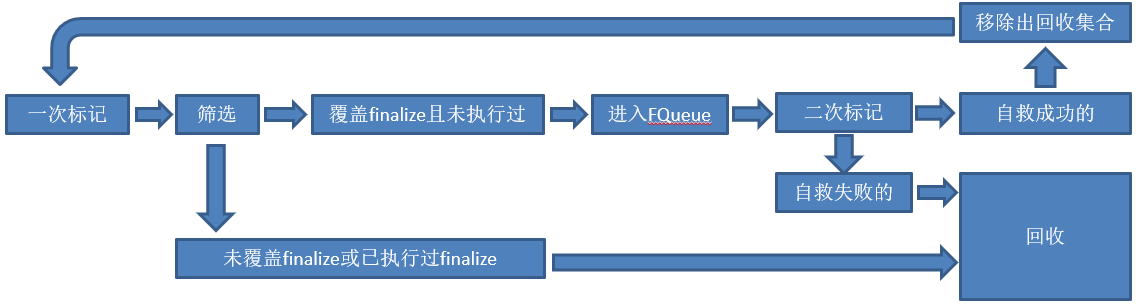
- 一次标记:即通过标记算法将对象标记为待回收状态,并进入一个待回收对象集合;
- 筛选:对一次标记之后的待回收对象进行过滤,如果该对象覆盖了finalize方法,并且该方法未执行过,则将该对象放入F-QUEUE;反之,对象没有覆盖finalize方法或者finalize方法已经被执行过了,该对象不会进行任何处理;
- F-QUEUE:一个队列,JVM会通过一个Finalizer线程去执行这个队列中对象的finalize方法,并且只保证该方法的执行,不保证该方法成功执行完成。因为若finalize方法有死循环,会造成FQUEUE后续未被执行对象的持续等待,导致整个内存回收系统崩溃。根据这个特点,对象可以在执行finalize方法时进行“自救”,所谓的自救,就是将对象重新与GC ROOTS相关联;
- 二次标记:GC会对FQUEUE中的对象进行额外的一次标记,若对象“自救”成功,则会从待回收对象集合中移除;若对象“自救”失败,它仍然会处于待回收对象集合中,等待真正被回收;
- 回收:对象通过垃圾收集进行回收,释放内存空间;
3.2.垃圾收集算法
在上一小节我们讲了对象标记相关的算法,本小节来了解一下垃圾收集算法。
3.2.1.标记-清除算法
标记-清除(mark-sweep)算法,是最基础的垃圾收集算法,它的思想比较简单,就是在“对象存活判定”标记出需要回收的对象后,统一回收(清除)这些对象的内存。
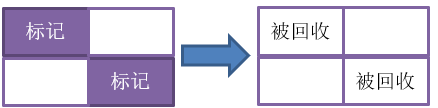
该算法简单有效,但是存在两个不足:首先是效率问题,标记和清除两个阶段的效率都不高,所谓效率不高,并非指的是自身的执行效率,而是指回收结果与耗时的效益比不高;其次是空间问题,标记-清除算法并未整理内存,会产生大量不连续的内存碎片,要分配较大对象时,可能无法找到足够的连续内存而不得不又触发一次GC。
3.2.2.复制算法
复制算法(copying)是对标记-清除算法的改进,其主要思想是将内存划分为不同的区域,包括“内存使用区”和“结果缓冲区”。每次只使用一部分内存,在该部分内存满了之后,将仍然存活的对象复制到另外一块区域上面,然后将之前使用过的内存区域全部清理掉,现代商业虚拟机都采用其回收新生代。
该算法大大提高了回收效率,也可以避免内存碎片。然而带来了新的问题:由于需要开辟一块内存空间作为每次回收结果的缓冲,因此可用内存无法达到100%,“结果缓冲区”的大小决定了内存有效的比率。
如何设置结果缓冲区的内存大小(比例)?将其设置为50%最能确保每次回收都有足够大小的缓冲区域存放回收结果,毕竟最差的情况就是所有对象都存活,然而内存浪费也太高了。根据IBM的研究,一般情况下,新生代中的对象98%都是“朝生夕死”的,也就是说,每次存活对象的比例并不会太高,我们只需要设置一小块内存作为“回收结果缓冲”即可,他们提出的解决模型如下,将内存划分为eden与2块suvivor:

- eden:主存储区,新对象的创建都在这块区域;
- survivor:分为两块,一块作为上次回收结果的“缓存”,一块作为下一次回收的“缓存”区域;
基于这种模型,每次回收时,将eden和上次回收结果的survivor中存活的对象复制进空闲的survivor,然后清理掉被回收的区域即可,简单的示意流程图见下:
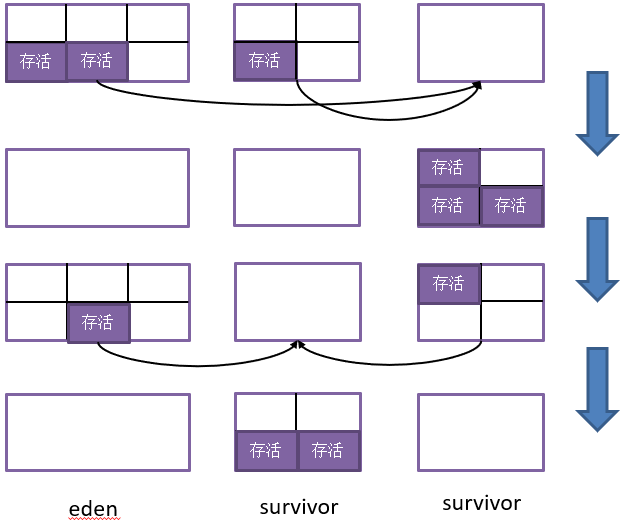
值得注意的是,对于eden-survivor模型,98%的对象可回收只是理想理论,在某些场景下,回收时存活对象的大小有可能大于空闲survivor。对于这种survivor空间大小不够用的情况,需要通过“分配担保”机制来保证对象能正确留存。所谓的分配担保,就是不够空间survivor存放的对象进入老年代。
3.2.3.标记-整理算法
在上一小节我们知道复制算法主要适合于新生代的回收,对于老年代这种对象存活率高的区域,因为每次都会复制大量对象,成本收益比较低,使用复制算法明显不合适;相反,标记-清除算法更适合老年代的特征,为了解决标记-清除算法的内存碎片问题,在此基础上,优化为标记-整理算法(mark-compact)。
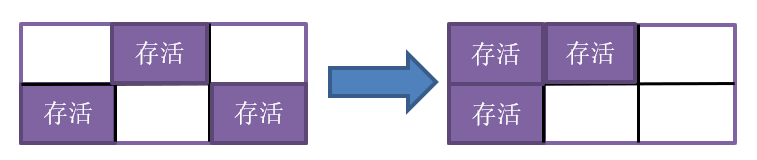
标记-整理算法主要思想是在标记对象后,将存活对象向内存的一端移动,然后清理掉端边界以外的内存,所谓的整理也可以理解为压缩。
3.2.4.总结
没有哪一种垃圾收集算法能够适用于所有情况,对于不同的堆内存区域(新生代、老年代),需要根据实际的对象特征,选择合适的算法。
| 算法 | 优点 | 缺点 | 适用区域 |
| 复制 | 效率较高,无内存碎片问题 | 1.内存利用率达不到100%;2.需要分配担保机制确保对象存活率较高时的内存分配; | 新生代(对象存活率低,复制成本低) |
| 标记-清除 | 简单有效 | 1.效率不高;2.有内存碎片问题; | 老年代(对象存活率高,无额外空间进行分配担保) |
| 标记-整理 | 标记-清除的改良,解决了内存碎片问题 | 1.同样存在效率问题;2.整理过程需要额外的时间开销; |