
事实上,目前还没有十全十美的排序算法,有优点就会有缺点,即使是快速排序法,也只是在整体性能上优越,它也存在排序不稳定、需要大量辅助空间、对少量数据排序无优势等不足。因此我们就来从多个角度来剖析一下提到的各种排序的长与短。
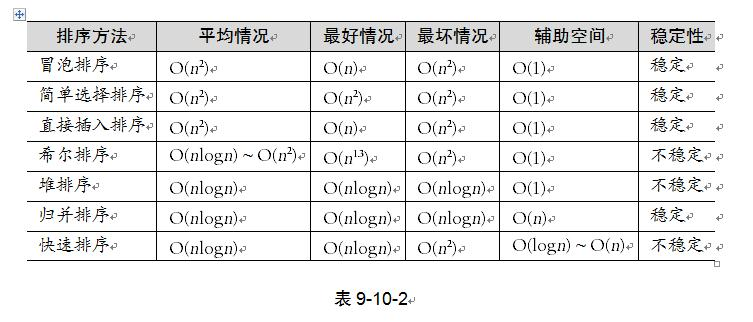
从算法的简单性来看,我们将七种算法分为两类
1) 简单算法:冒泡、简单选择、直接插入。
2) 改进算法:希尔、堆、归并、快速。
从平均情况来看,显然后三种改进算法要胜过希尔排序,并远远胜过前三种简单算法。
从最好情况看,反而冒泡和直接插入排序要更胜一筹,也就是说,如果你的待排序序列总是基本有序,反而不应该考虑四种复杂的改进算法。
从最坏情况看,堆排序与归并排序又强过快速排序以及其他简单排序。
从这三组时间复杂度的数据对比中,我们可以得出这样一个认识。堆排序和归并排序就像两个参加奥数考试的优等生,心理素质强,发挥稳定。而快速排序像是很情绪化的天才,心情好时表现极佳,碰到较糟糕环境会变得差强人意。但是他们如果都来比赛计算个位数的加减法,它们反而算不过成绩极普通的冒泡和直接插入。
从空间复杂度来说,归并排序强调要马跑得快,就得给马吃个饱。快速排序也有相应的空间要求,反而堆排序等却都是少量索取,大量付出,对空间要求是O(1)。如果执行算法的软件所处的环境非常在乎内存使用量的多少时,选择归并排序和快速排序就不是一个较好的决策了。
从稳定性来看,归并排序独占鳌头,我们前面也说过,对于非常在乎排序稳定性的应用中,归并排序是个好算法。
从待排序记录的个数上来说,待排序的个数n越小,采用简单排序方法越合适。反之,n越大,采用改进排序方法越合适。这也就是我们为什么对快速排序优化时,增加了一个阀值,低于阀值时换作直接插入排序的原因。
从上表的数据中,似乎简单选择排序在三种简单排序中性能最差,其实也不完全是,比如说如果记录的关键字本身信息量比较大(例如关键字都是数十位的数字),此时表明其占用存储空间很大,这样移动记录所花费的时间也就越多,我们给出三种简单排序算法的移动次数比较,如表9-10-3所示。
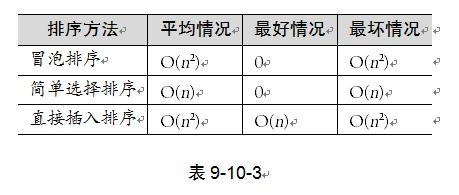
你会发现,此时简单选择排序就变得非常有优势,原因也就在于,它是通过大量比较后选择明确的记录进行移动,有的放矢。因此对于数据量不是很大,而记录的关键字信息量较大的排序要求,简单排序算法是占优的。另外,记录的关键字信息量大小对那四个改进算法影响不大。
总之,从综合各项指标来说,经过优化的快速排序是性能最好的排序算法,但是不同的场合我们也应该考虑使用不同的算法来应对它。
|
1
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 |
#include <iostream>
using namespace std; void Swap(int array[], int i, int j) { int tmp = array[i]; array[i] = array[j]; array[j] = tmp; } void BubbleSort1(int array[], int len) { int exchange = 1;//表示没有排序 for (int i = 0; i < len && exchange; ++i) { exchange = 0; for (int j = len-1; j >i; j--) { if(array[j] < array[j-1]) { Swap(array, j, j-1); exchange = 1; } } } } void BubbleSort2(int array[], int len) { for (int i = 0; i < len; ++i) { for(int j = 0; j<len-i-1; j++) { if (array[j] > array[j+1]) { Swap(array, j, j+1); } } } } void SelectSort(int array[], int len) { for (int i = 0; i < len; ++i) { int min = i; for(int j = i+1; j < len ; j++) { if (array[min] > array[j]) { min = j; } } Swap(array,i, min); } } void InsertSort(int array[], int len) { for (int i = 1; i <len; i++) { int k = i;//待插入的位置 int tmp = array[k]; for(int j = i-1; (j>=0) && (tmp < array[j]);j--) { array[j+1] = array[j]; k = j; } array[k] = tmp; } } void ShellSort(int array[], int len) { int gap = len; do { gap = gap/3+1; for (int i = gap; i < len; ++i) { int k = i; int tmp = array[k]; for(int j=i-gap; (j>0)&& (tmp<array[j]);j--) { array[j+gap] = array[gap]; k = j; } array[k] = tmp; } }while(gap>1); } void Merge(int src[], int des[], int low, int mid, int high) { int i = low; int j = mid+1; int k = low; while((i<=mid) && (j<= high)) { if (src[i] < src[j]) { des[k++] = src[i++]; } else { des[k++] = src[j++]; } } while(i <= mid) { des[k++] = src[i++]; } while(j <= high) { des[k++] = src[j++]; } } void MSort(int src[], int des[], int low, int high , int len) { if (low == high) { des[low] = src[low]; } else { int mid = (low+high)/2; int *space = (int*)malloc(sizeof(int)*len); if (space == NULL) { return; } MSort(src, space, low, mid, len); MSort(src, space, mid+1, high, len); Merge(space, des, low ,mid, high); free(space); } } void MergeSort(int array[], int len) { MSort(array, array, 0, len-1, len); } //-----快速排序------------ int partition(int array[], int low, int high) { int pv = array[low]; while(low < high) { while((low < high) && (array[high] > pv)) { high--; } Swap(array, low, high); while((low < high) && (array[low] <= pv)) { low++; } Swap(array, low, high); } return low; } void QSort(int array[], int low, int high) { if (low < high) { int pivot = partition(array, low, high); QSort(array, low , pivot-1); QSort(array, pivot+1, high); } } void QuickSort(int array[], int len) { QSort(array, 0, len-1); } void Printf(int array[], int len) { for (int i = 0; i < len; ++i) { cout << array[i] << " "; } cout << endl; } int main() { int array[] = {9,8,6,5,3,7}; int len = sizeof(array)/sizeof(int); cout << "冒泡排序从后往前...." << endl; BubbleSort1(array, len); Printf(array, len); cout << "冒泡排序从前往后...." << endl; BubbleSort2(array, len); Printf(array, len); cout << "选择排序...." << endl; SelectSort(array, len); Printf(array, len); cout << "插入排序...." << endl; InsertSort(array, len); Printf(array, len); cout << "希尔排序...." << endl; ShellSort(array, len); Printf(array, len); cout << "归并排序...." << endl; ShellSort(array, len); Printf(array, len); cout << "快速排序...." << endl; QuickSort(array, len); Printf(array, len); return 0; } 
冒泡排序从后往前.... 3 5 6 7 8 9 冒泡排序从前往后.... 3 5 6 7 8 9 选择排序.... 3 5 6 7 8 9 插入排序.... 3 5 6 7 8 9 希尔排序.... 3 5 6 7 8 9 归并排序.... 3 5 6 7 8 9 快速排序.... 3 5 6 7 8 9 [Finished in 0.9s] |
|
1
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 |
//*********排列组合*****
void Printf(char array[], int len) { for (int i = 0; i < len; ++i) { cout << array[i] << " "; } cout << endl; } void Swap(char array[], int i, int j) { int tmp = array[i]; array[i] = array[j]; array[j] = tmp; } //排列组合 void Permutation(char array[], int m, int n) { if (m == n) { for (int i = 0; i <= m; ++i) { cout << array[i]; } cout << endl; } else { for (int i = m; i <= n; ++i) { Swap(array, i, n); Permutation(array, m + 1, n); Swap(array, i, n); } } } |
