深度学习基础

摘要：本文主要介绍了深度学习中的一些基础知识和CNN的相关内容。

1、关于目标函数的选取

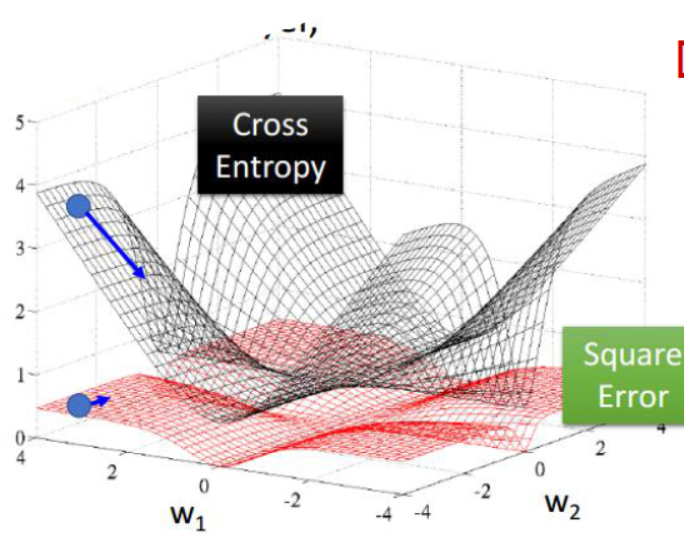
目标函数用于衡量训练出来的模型的输出值和给定样本数据实际输出值的误差。目标函数会直接参与到误差的反向传播的计算当中，一个较好的目标函数会对各层的权重的调整起到更好的效果，所以选择好的目标函数尤为重要。下面列举出两种目标函数：

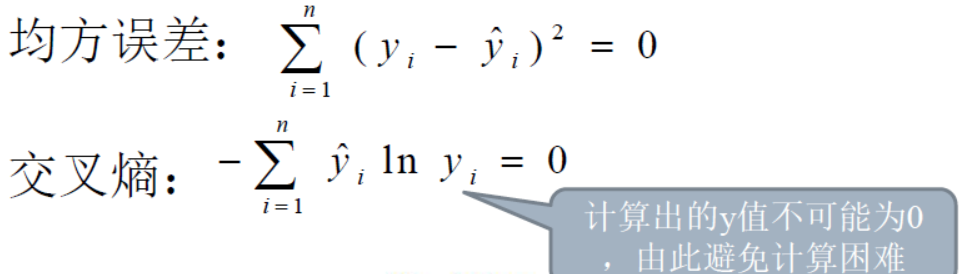
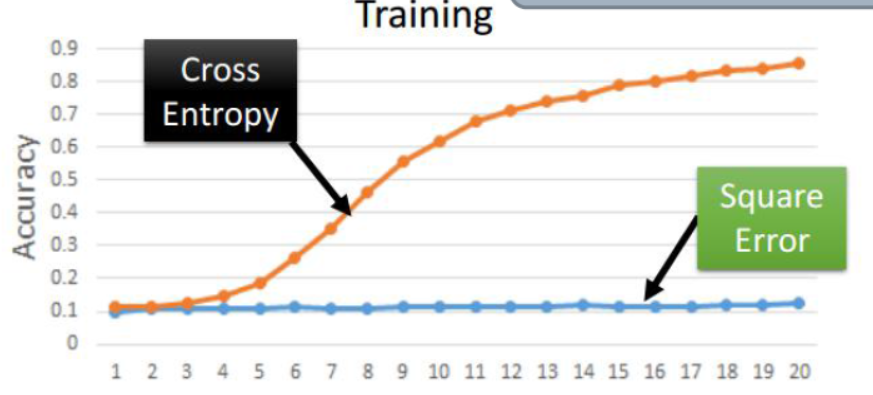
在上面两种比较常见的目标函数的对比中，我们可以清楚的看到，交叉熵目标函数的图像更加陡峭，因此移动相同的步数，那么目标函数的变化也就更加明显，那么也就更有利于寻找最小值（最优值），最终确定相应的模型权重。

2、关于全连接层Softmax

Softmax是神经网络的最后一层，用于处理经过各个层计算后得到的最后结果。如下图：

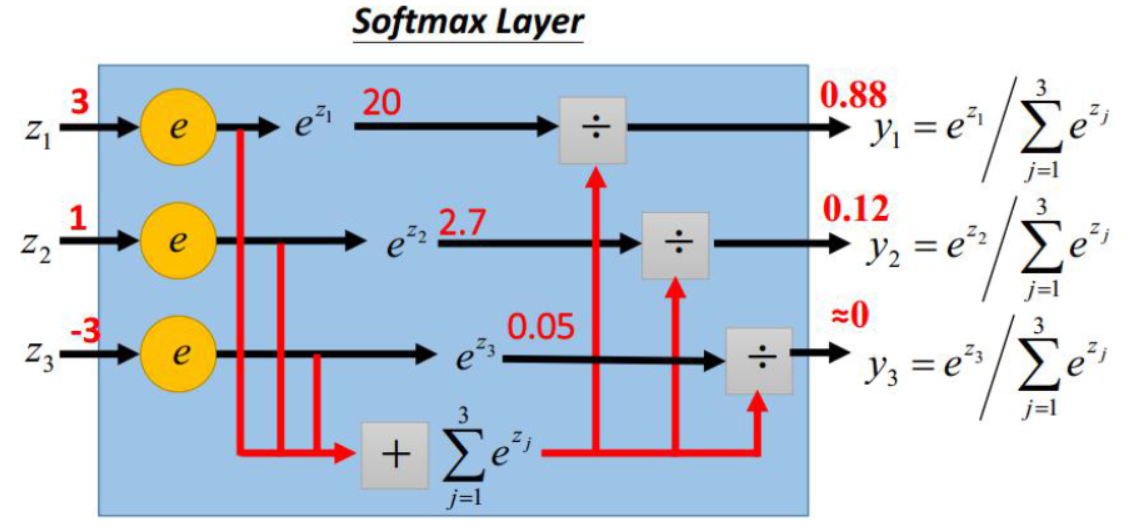
 在上面的图中，z代表经过各层计算得到的输出值，将z值带入上面的逻辑计算中，最后得到了的输出值有这样的特点：将原来的输出结果映射到了0-1范围内，并且这些值相加为1。

那么为什么要进行这样做呢？

• 经过Softmax处理得到的输出值可以用在以交叉熵作为目标函数的情况中。
• 利用概率的形式进行处理，更加明确了各个输出值对精度的影响状况，进而更有利于对各层权重进行调整。

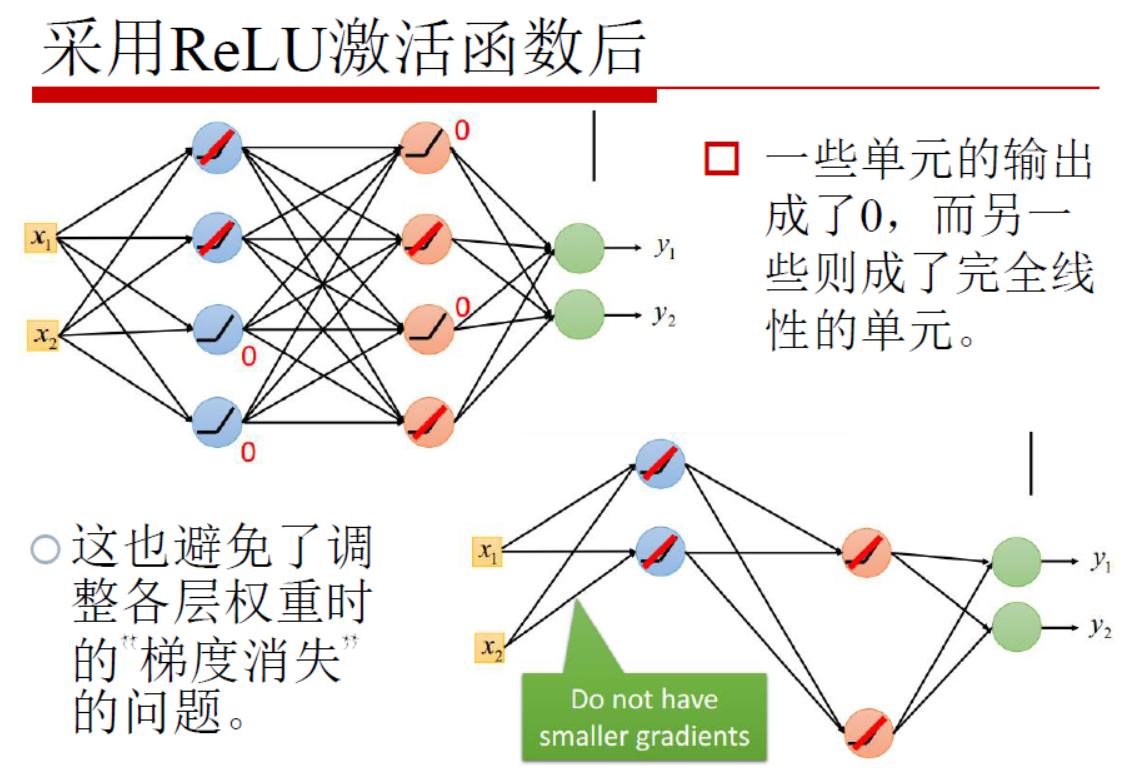
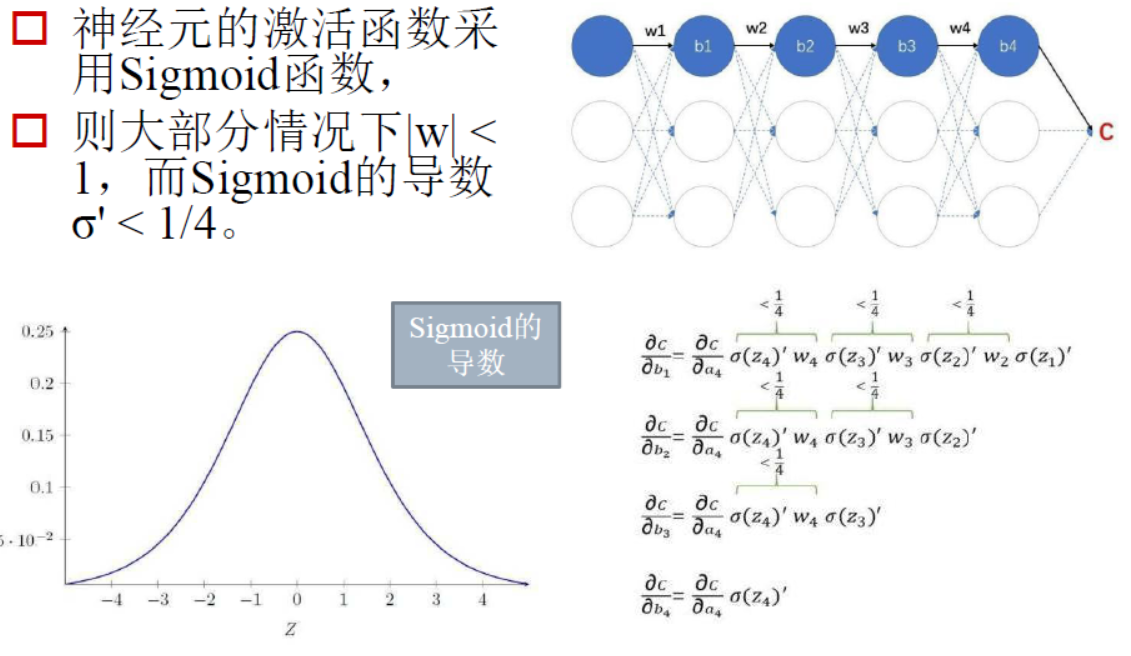
3、采用RELU激活函数，而不采用Sigmoid函数的原因

在梯度下降过程中，会对激活函数求导，Sigmoid函数求导之后的峰值为0.25，而且在调整权重的过程中w的绝对值一般都是小于1的，这样就会导致最终求得的梯度下降值非常小，这毫无疑问会导致迭代效率大打折扣。而RELU函数则可以较好地解决这样的问题，如下图：

根据上图，总结RELU函数的优点如下：

• 对于深度神经网络，sigmoid函数反向传播时，很容易就出现梯度消失的情况（比如sigmoid函数接近饱和区时，变换太缓慢，导数趋于0，这种情况就会造成信息消失），从而无法完成深层网络的训练。

• 使用Relu会使部分神经元为0，这样就造成了网络的稀疏性，并且减少了参数之间的相互依赖关系，缓解了过拟合问题的发生【因为早期的机器学习主要是神经网络方面演化的，是想用机器模拟人类大脑的工作，而大脑参与某一件事的运算时，是由一些基本的神经元发挥作用，就是由一些基本的特征组合就可以拼接出高阶的特征表达，所以稀疏一些比较好。】

• 采用sigmoid等函数，算激活函数（进行指数运算时），计算量大。反向传播误差传递时，求导涉及除法，计算量非常大，而采用Relu激活函数，整个过程的计算量就会节省很多。

4、关于学习步长的调整问题

在进行梯度下降时，如果步长太大，那么在学习过程中会导致目标函数的值在两峰之间跳来跳去，而无法找到最优解。而当步长太小时，效率又太低。所以理想的方法是每迭代几次就进行一次步长的调整。如下图：

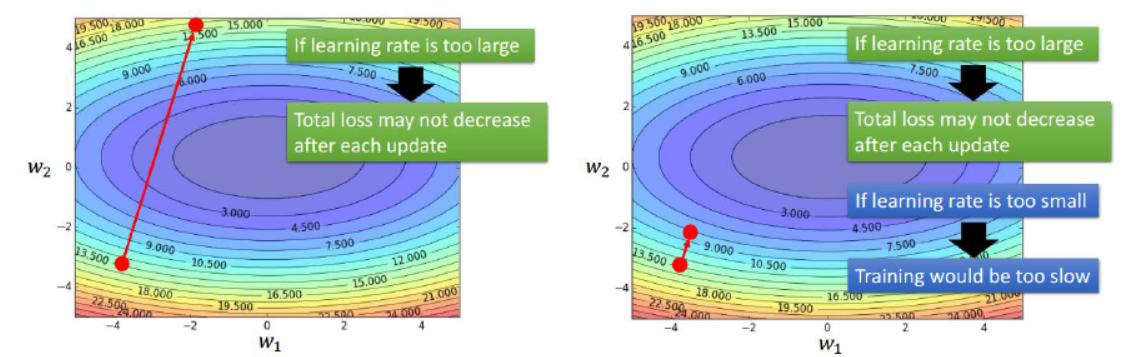
除了上面提到的问题之外，在深度学习过程中还可能会遇到马鞍面的情况，在马鞍面处，基本所有方向的梯度变化均为0，这样就导致了权重变化的停滞。

解决方案：

1、借助动量（冲量）思想（momentum）：

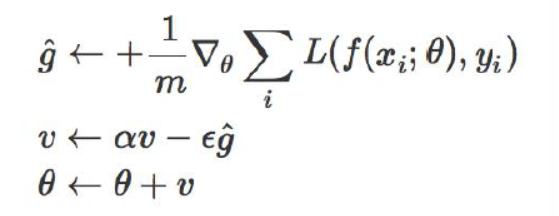
 在上面的例子中，g就是梯度，v就是动量，前面的α是一个衰减系数，ε就是步长，那么每一次得到的新v就是一个携带有冲量的梯度下降量，这样就可以防止马鞍面问题。但是也有一个问题，累加效应会让这个下降的量越来越大。

后来又有学者对这个模型进行了一个微调——计算梯度的时候首先进行一个估计（nesterov momentum），然后再计算误差（如下图），事实证明，效果会略好些。

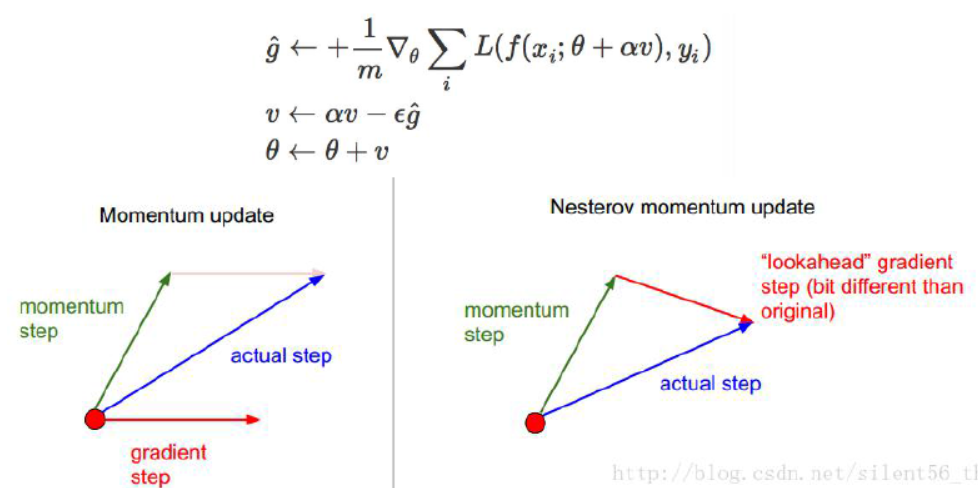
 2、在上面的例子中，可以解决的问题主要是越过马鞍面的问题，但是依然不能解决步长选择的问题，于是出现了下面的改进的方法（adagrad），这样的方法使得不同的梯度具有不同的步长，当曲面比较陡峭时选择较小的步长，比较平缓时选择比较大的步长：

 在上面的例子中，看似没有问题，但是正如图上指出的，r的值会越来越大，这样就实现不了步长随斜率改变的设想，但是另一方面这样也是合理的：刚开始步长较大可以快速下降梯度，之后步长减小，可以防止谷底抖动，方便找到极小值。

既然上面的例子有“累加效应”，那么只要去除这种效应，就可以实现更好的效果，于是出现了更好的改进（RSMprop）：

3、最后一种方法是自适应距估计(Adam)，如下图：

各种方法最终对梯度下降的影响效果图如下：

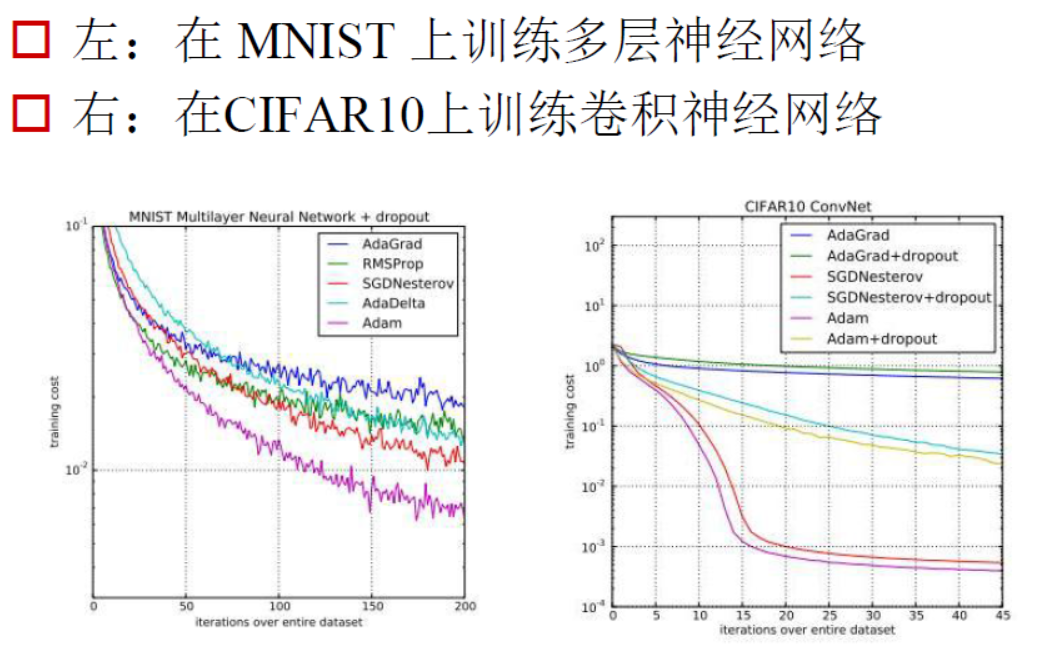
 对于梯度下降算法的选择，不能够一概而论，主要依据数据的特点来定。

5、关于Batch Normalization的理解

实际上进行深度学习训练的时候，每一次都是按照一定的比例选择一部分数据进行训练。这样的模式就导致了每一次迭代过程中数据都是有改变的。在上面的第四点中提到，对于梯度下降的方法，其实要根据数据的疏密程度来定。综合上面的原因，由于每次迭代数据不同，那么每次就要选择不同的梯度下降方法，这样就为训练过程带来了很大的麻烦，因此，后来有学者提出了Batch Normalization算法。具体如下：

上面的算法的前面三步实际上是将数据进行了误差的归一化处理，最后一步是为了将数据进行一定程度的还原，经过这样的处理之后，再进行梯度下降算法的处理，就会有效避免迭代中的算法算则问题。

6、关于过拟合问题的处理

有时候数据量太少，但是神经网络中的权重参数太多，经过很多次迭代训练之后就会出现过拟合的情况，处理过拟合的发生，可以采用下面这些方法：

• 防止过度训练，在训练早期就停止训练

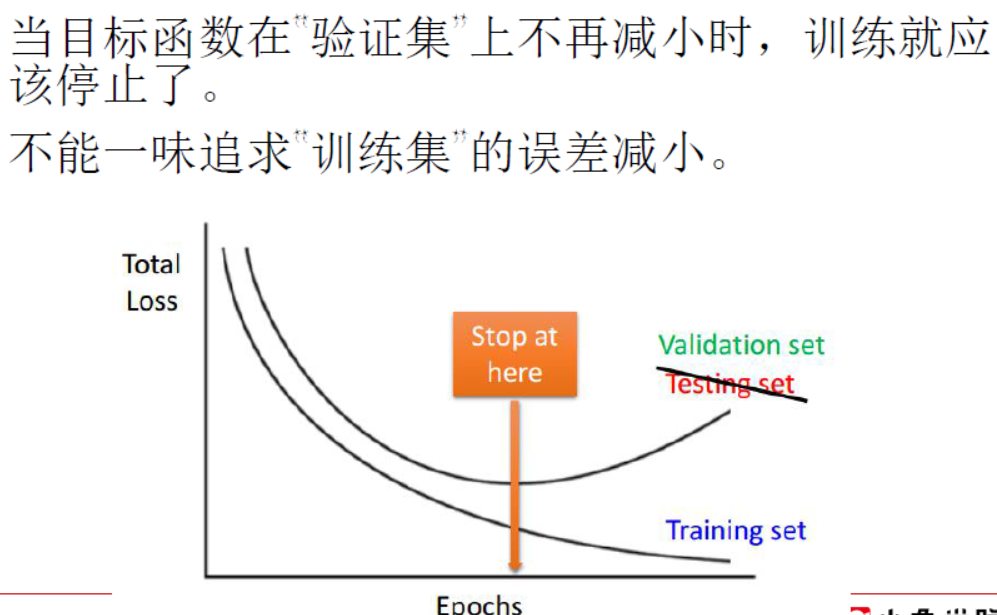
• 进行权重衰减

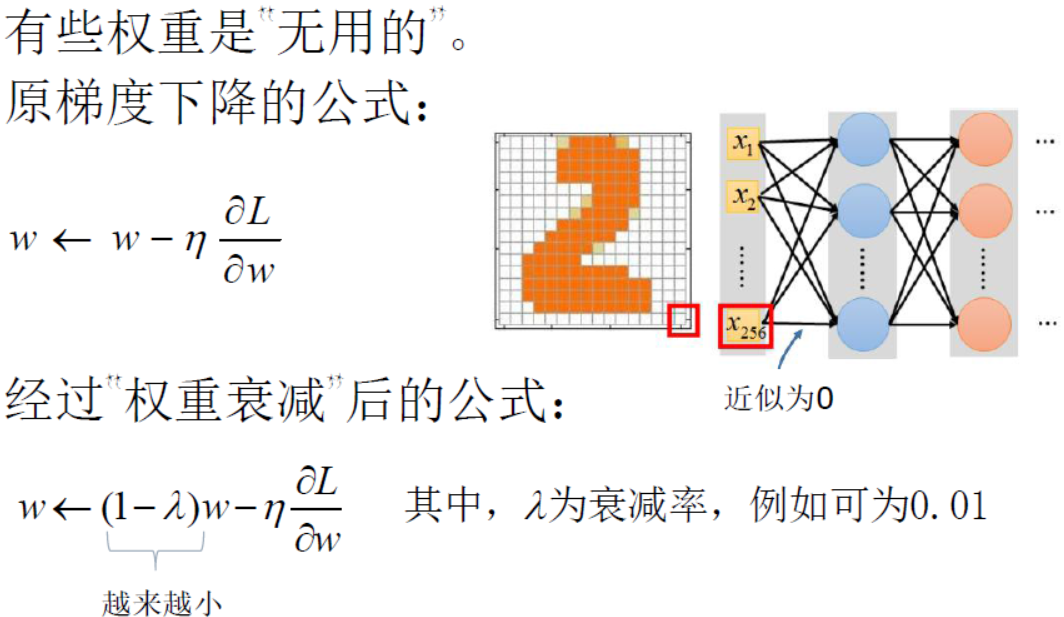
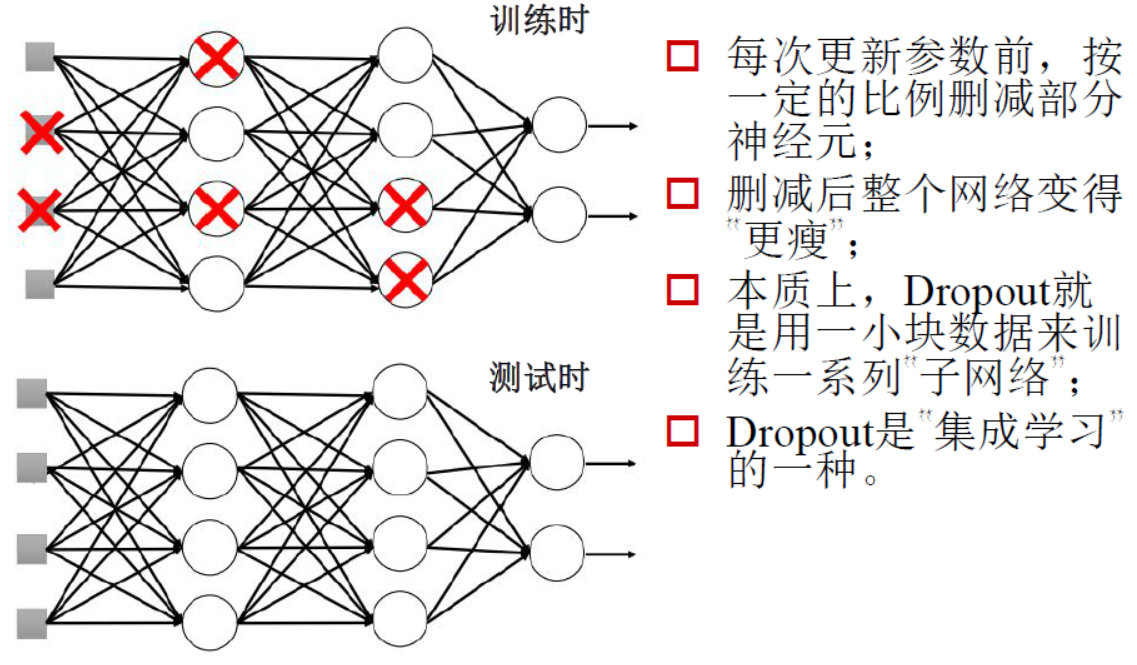
• 删除无用权重Dropout方法

在训练时，删除一些无用权重，测试时还可以弱化一些权重

 7、卷积神经网络（CNN）的层

卷积神经网络主要分成了卷积层、池化层和全连接层，下面对这些层进行一一介绍：

• 卷积层

总而言之，卷积层就是对图像进行卷积操作之后再将卷积的结果送给激活函数进行处理。具体的特点如下：

首先是卷积操作特点：

1. 图像是彩色图像，均是RGB结构，那么对应的卷积核也是三层
2. 不同于一般的图像滤波，卷积核上的参数不是固定的，这里的卷积核参数是随着训练迭代不断改变的，也就是卷积核充当各层之间的权重这一角色
3. RGB图像的三个通道的每一层都含有不止一个卷积核，而且每一个卷积核都对应一个输出通道，因此输出图像的通道数是由卷积核的总个数来决定的

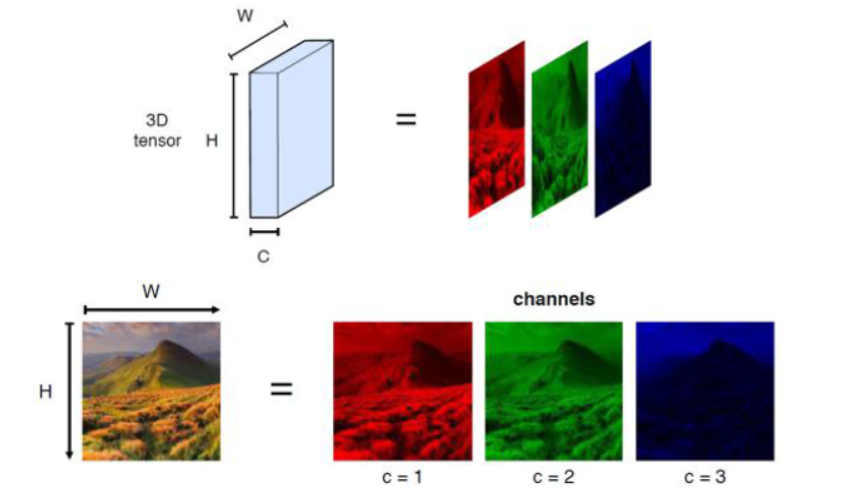
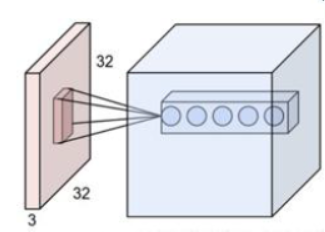
三通道的RGB图像	多个卷积核，最终输出多通道图像结果
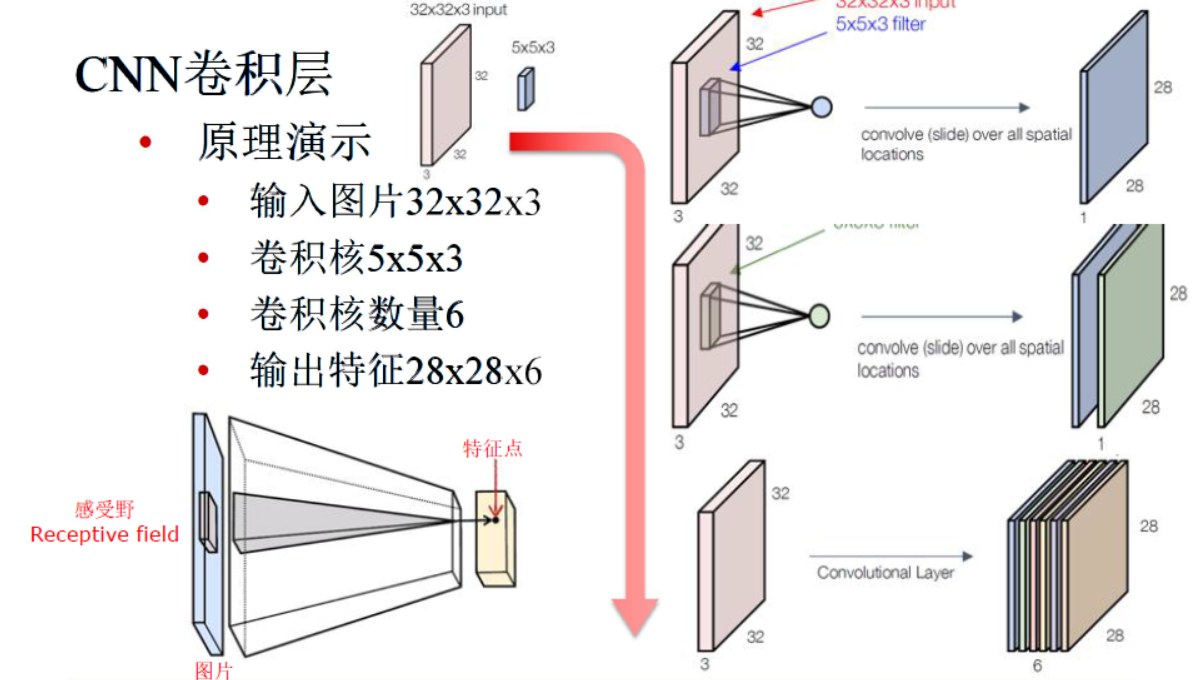
举例说明

激活函数的使用特点：

一般来讲使用ReLU函数

卷积的步长大于1，这样可以对图像降维（也就是使得图像变小）

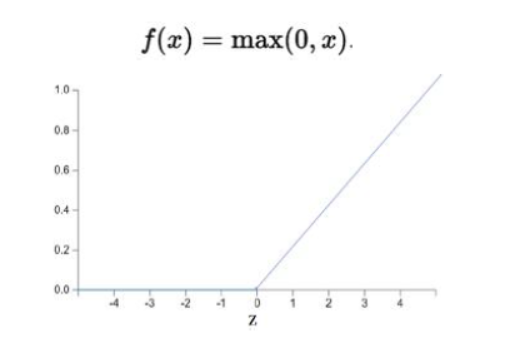
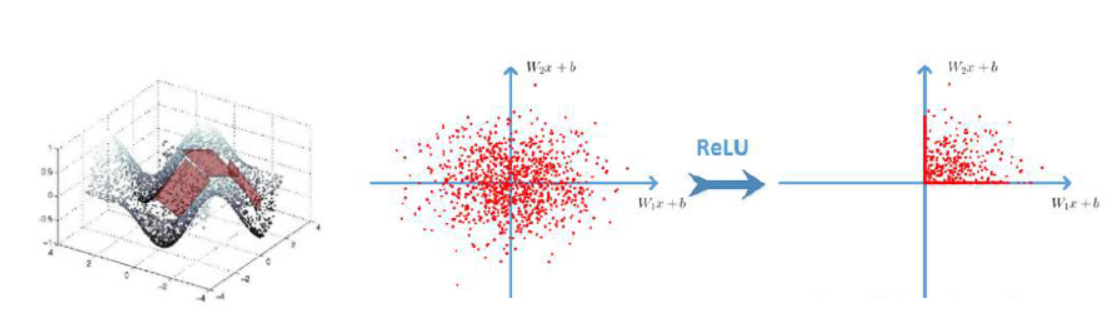
激活函数	使用ReLU函数的效果
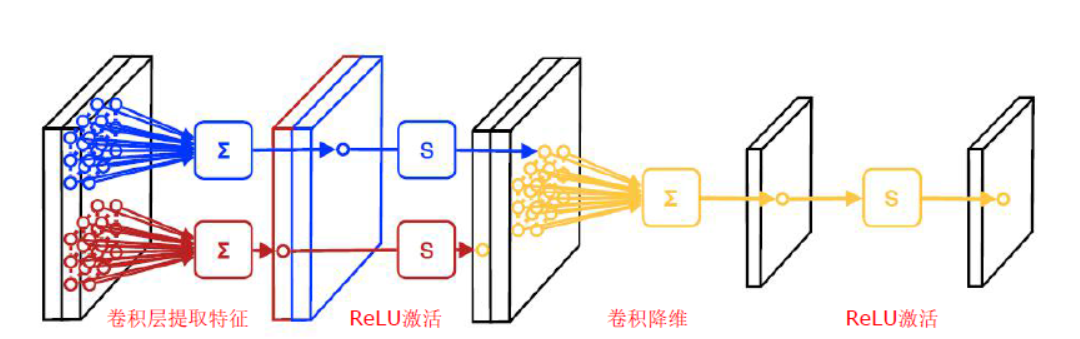
卷积层所完成的工作

• 池化层

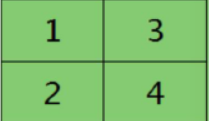
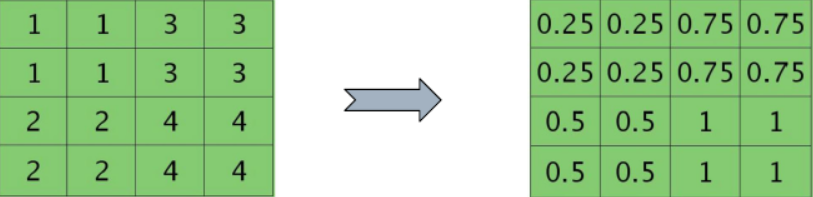
池化层所做的事情比较简单，就是降维，并没有参数需要调整学习，一般来讲有最大化池化和平均池化，根据经验，最大化池化的效果更好一些：

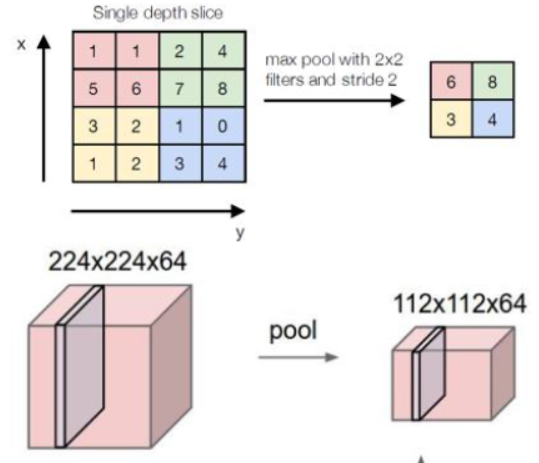
•  Softmax层

这一层和之前介绍过的全连接层的Softmax层一样，就是归一化之后形成一个概率值的组合。

 8、卷积神经网络（CNN）的误差反向传播

首先是池化层的误差反向传播：

对应之前讲到的残差计算公式，可以知道在卷积神经网络中的残差计算公式如下：

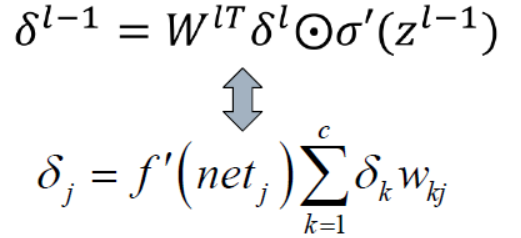
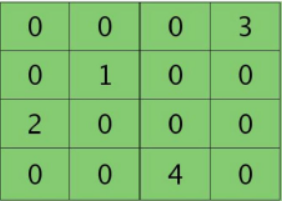
 其实对于池化层而言，只是进行了最大值提取或者是进行了平均值提取，这一层并没有进行权重计算。所以这一层的残差要想进行回传，应该先进行恢复（下采样）：

池化残差	恢复图残差
池化残差	恢复图残差

利用下面的公式，就可以求取前面一层卷积层的残差如下：

 有了上面的残差，和这一个卷积层的输入相乘就会得到权重改变量。

接下来是卷积层的误差反向传播：

对照之前讲到的公式，首先根据链式求导法则，利用下面的方法可以求取残差：

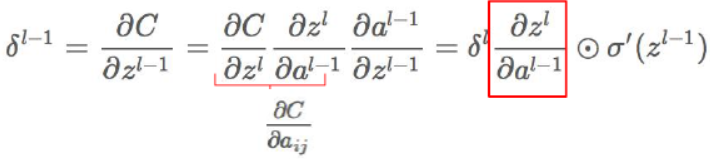
 其中的输出z如下：

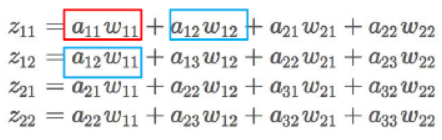
那么进行如下的计算：

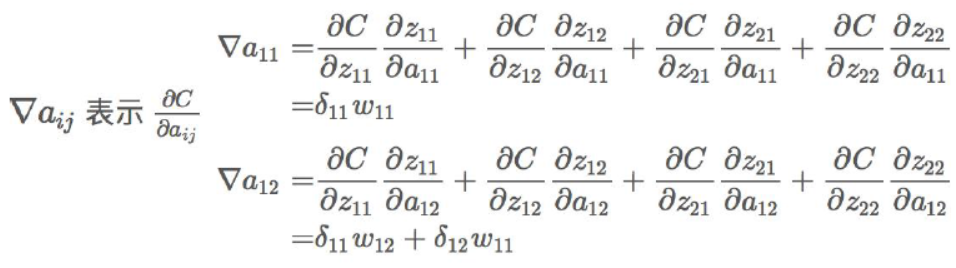
 根据上面式子的结果，可以得到如下形式的结论，注意这里是卷积操作：

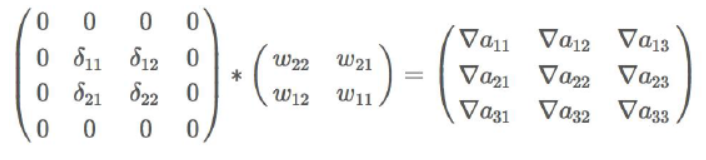
 那么：

有了上面的残差，和这一个卷积层的输入相乘就会得到权重改变量。

另外，当卷积层前面一层是池化层的话会有如下的情况：

9、卷积神经网络误差反向传播的例子
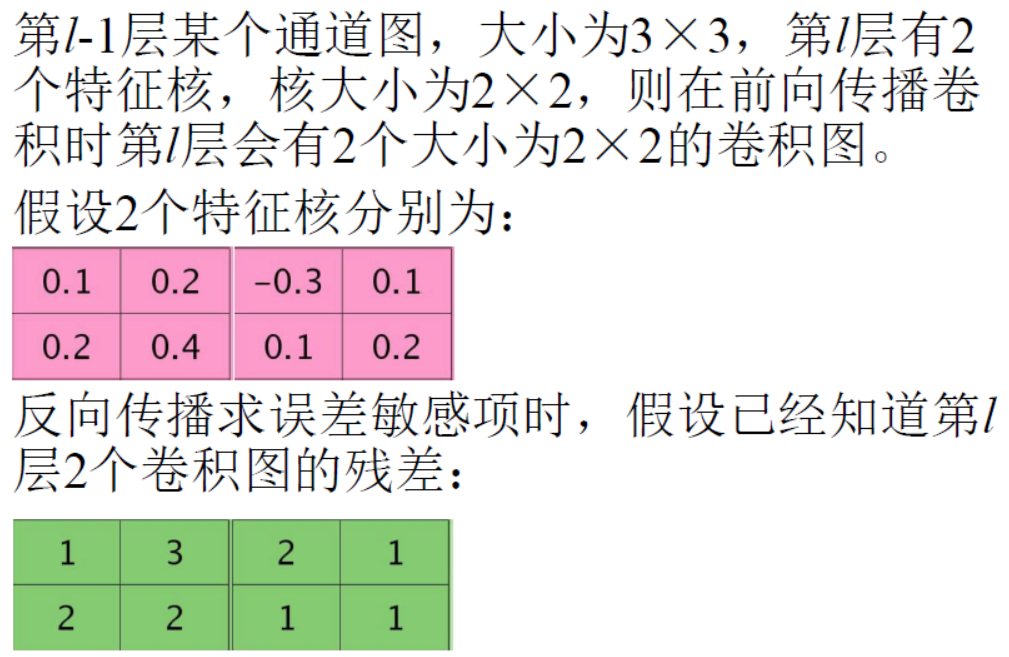
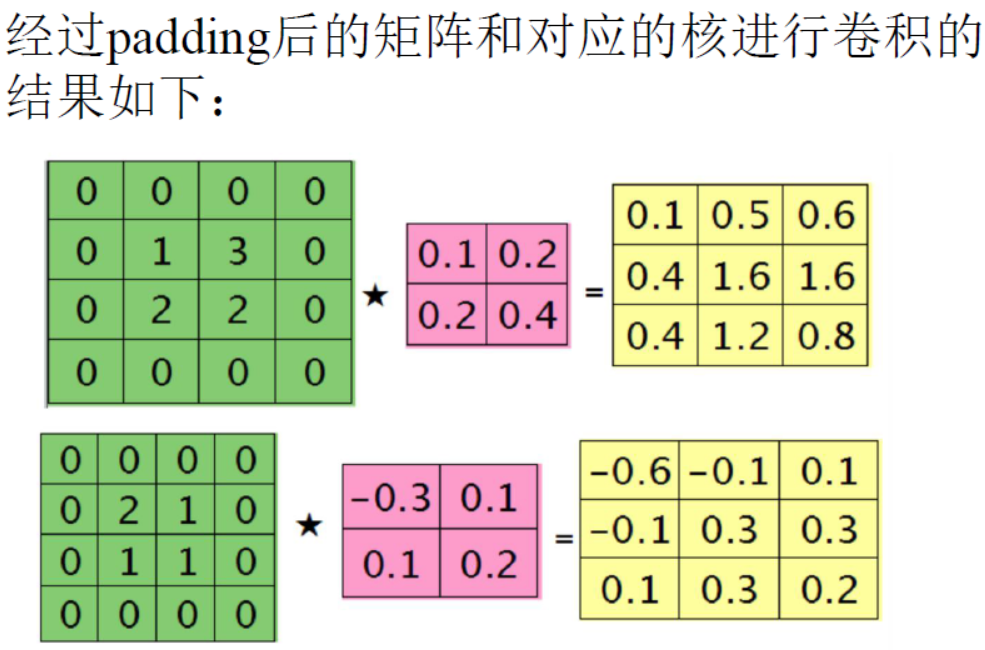
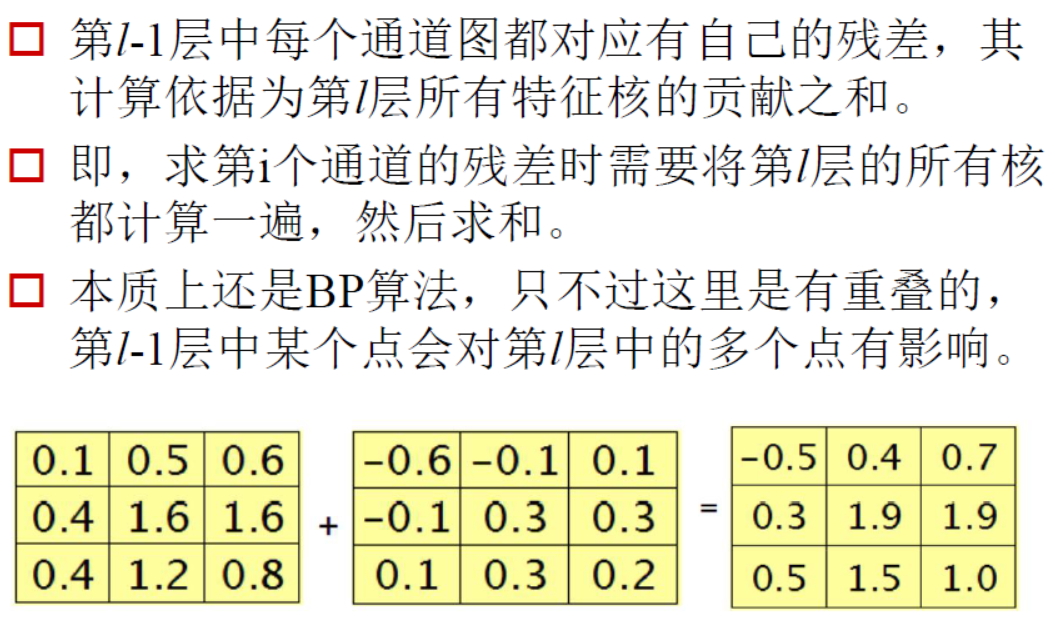