数据结构：关键路径，利用DFS遍历每一条关键路径JAVA语言实现

     这是我们学校做的数据结构课设，要求分别输出关键路径，我查遍资料java版的只能找到关键路径，但是无法分别输出关键路径

     c++有可以分别输出的，所以在明白思想后自己写了一个java版的

     函数带有输入函数也有已经存进去的图

    

    如上图关键路径被分别输出（采用了DFS算法）：

     例：AOE 图如下：

  

      算法设计如下：

       1. 首先，要求关键路径，要先要先写拓扑排序，如果图中有环，就无法进行关键路径的求解，直接跳出。

   拓扑排序：利用栈stack，先将入度为0事件节点的加入栈中，然后编历后面的活动节点，每次给活动节点的入度减一，然后将入度为0的加入栈       stack中，每次出栈的加入栈stack中，stack1中的元素拓扑排序的逆序，然后根据核心算法：

    if(etv[p.getData()]+p1.getInfo()>etv[p1.getAdjvex()]){
    etv[p1.getAdjvex()]=etv[p.getData()]+p1.getInfo();
    }

计算出事件的最早发生时间的事件存入etv

    然后根据count来判断图中有没有回路。

2. 然后对拓扑排序的逆序求事件的最晚发生时间，根据核心法：

     if (ltv[p1.getAdjvex()]-p1.getInfo()<ltv[p.getData()]){
    ltv[p.getData()]=Math.abs(ltv[p1.getAdjvex()]-p1.getInfo());
        }

    算出事件的最晚发生时间存入数组ltv中。

3. 接着求活动的最晚发生时间el和活动的最早发生时间ee

     　　　　ee=etv[i];
　　　　el=ltv[pn.getAdjvex()]-pn.getInfo();

    当ee和el相等的时候，本活动就为关键活动，关键路径算出来了。

     解决输出每条关键路径：

4. 输出每一条关键路径：利用DFS算法（回溯算法），

图在遍历以前已经将关键路径用visited数组标记了，

故遍历的时候只遍历关键路径，

原理如图：

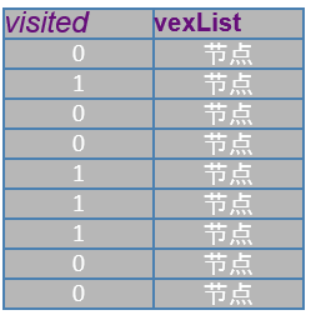
当visited为0的时候为关键节点，然后遍历此节点进入递归：

while (p!=null){
     if(visited[p.getAdjvex()]!=1){
        /**
         * 是关键路径就入栈
         */
        stack2.push(p);
        DFS(p.getAdjvex());
        /**
         * 遇见死路回退的时候出栈
         */
        stack2.pop();
    }

本算法类似走迷宫，并且每走一个点，就把这个点入栈，并且将visited数组中的本节点的值存为1，代表遍历过了：

　　　　　　　　　　　　　　　　visited[k]=1;

然后递归进入下一个节点，遇见终点就先遍历并输出栈中的元素：

if(k==finall) {
     for (int i=0;i<stack2.size;i++) {
        System.out.print(stack2.peekTravel(i).getName() + "->");
        }
    } 

一边退回一边出栈：

  DFS(p.getAdjvex());
        /**
         * 遇见死路回退的时候出栈
         */
        stack2.pop();

即栈中元素只到分岔点，退回上一次的分岔点，然后递归进入下一条路，直到遍历结束，然后输出了全部的关键路径。

   　　　　　　　　　　　　　　

DFS算法全部代码：

/**
 * 为了输出每条关键路径用到DFS算法
 * @param k 起点再数组中的下标
 */
public void DFS(int k){
    visited[k]=1;
    lineNode p=new lineNode();
    p=vexList[k].getNext();
    /**
     * 终点永远是关键节点
     */
    visited[finall]=0;
    /**
     * 如果走到终点遍历栈的元素
     */
    if(k==finall) {
        for (int i=0;i<stack2.size;i++) {
            System.out.print(stack2.peekTravel(i).getName() + "->");
        }
    }
    /**
     * 遍历节点后面的链表
     */
    while (p!=null){
        if(visited[p.getAdjvex()]!=1){
            /**
             * 是关键路径就入栈
             */
            stack2.push(p);
            DFS(p.getAdjvex());
            /**
             * 遇见死路回退的时候出栈
             */
            stack2.pop();
        }
        System.out.println();
        p=p.getNext();
    }
}

DFS算法流程图：

　　　　　　　　　　　

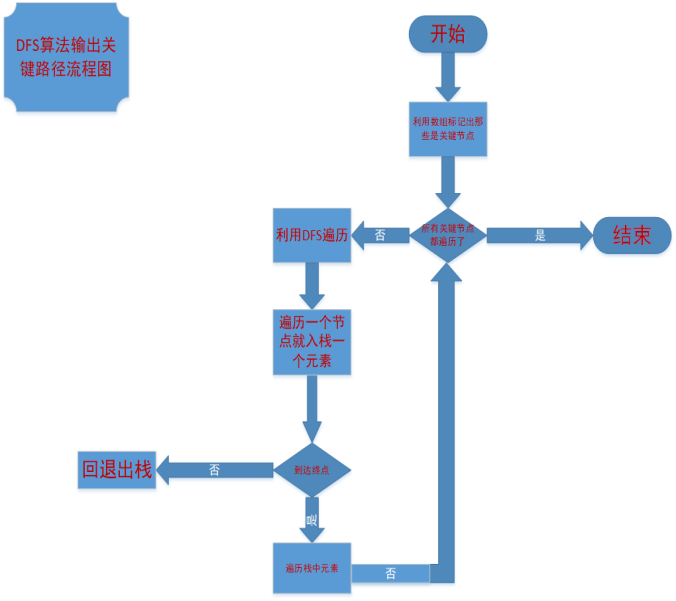
 　　　　　　　　　　　　　　　　　　（流程图有问题，左端回退出栈少了循环）

　源代码如下：

    　　

package dataproject.importanRoad;
import dataproject.stack.myArrayStack;
import java.util.Scanner;
/**
 * @author 李正阳  17060208112
 */
public class lessonWord {
    /**
     * 顶点数组
     */
    private vertexNode[] vexList;
    /**
     * etv 事件最早发生时间(即顶点）
     * ltv 事件最晚发生时间
     */
    private int etv[], ltv[];
    /**
     * 拓扑排序所用到的栈
     */
    private myArrayStack<vertexNode> stack=new myArrayStack<>();
    private myArrayStack<vertexNode> stack1=new myArrayStack<>();
    /**
     * 为了输出关键路径，标明哪些是关键节点
     */
    static int MAX_VERTEXNUM = 100;
    static int [] visited = new int[MAX_VERTEXNUM];
    /**
     *关键路径用到的栈队，数组
     */
    private myArrayStack<lineNode> stack2=new myArrayStack<>();
    private static int finall;
    /**
     * 使用键盘输入来构建图构建图
     */
    public void createGraph(){
        vertexNode pl1=new vertexNode();
        lineNode pl=new lineNode();
        int n;
        Scanner in=new Scanner(System.in);
        System.out.println("请输入共有多少个节点：");
        n=in.nextInt();
        vexList = new vertexNode[n];
        for (int i=0;i<n;i++){
            int p;
            /**
             * 构建节点
             */
            System.out.println("节点"+(i+1)+"节点存在数组中的位置 "+"节点名字");
            vertexNode v= new vertexNode( in.nextInt(), null, in.nextLine());
            pl1=v;
            pl=v.getNext();
            System.out.println("请输入此节点后有多少个边：");
            p=in.nextInt();
            for (int j=0;j<p;j++){
                /**
                 * 构建活动即事件
                 */
                System.out.println("边"+(j+1)+"后续节点在数组中的位置 "+"权值 "+"边的名字");
                lineNode a= new lineNode(in.nextInt(),in.nextInt(), in.nextInt(), null,in.next(),false);
                if(j==0){
                    pl1.setNext(a);
                    pl=pl1.getNext();
                }else {
                    pl.setNext(a);
                    pl=pl.getNext();
                }
            }
            vexList[i]=v;
        }
    }

    /**
     * 存储下的图，和我画出的图一样，方便测试
     */
    public void craeteGraph() {
        /**
         * 所有节点即事件
         */
        vertexNode v1 = new vertexNode( 0, null, "v1");
        vertexNode v2 = new vertexNode( 1, null, "v2");
        vertexNode v3 = new vertexNode(2, null, "v3");
        vertexNode v4 = new vertexNode( 3, null, "v4");
        vertexNode v5 = new vertexNode(4, null, "v5");
        vertexNode v6 = new vertexNode(5, null, "v6");
        vertexNode v7 = new vertexNode(6, null, "v7");
        vertexNode v8 = new vertexNode(7, null, "v8");
        vertexNode v9 = new vertexNode(8, null, "v9");
        /**
         * v1节点
         * a1活动，a2活动，a3活动
         */
        lineNode v12 = new lineNode(0,1, 6, null,"a1",false);
        lineNode v13 = new lineNode(0,2, 4, null,"a2",false);
        lineNode v14 = new lineNode(0,3, 5, null,"a3",false);
        lineNode a12=new lineNode(0,9,5,null,"a12",false);
        v1.setNext(v12);
        v12.setNext(v13);
        v13.setNext(v14);
        v14.setNext(a12);
        /**
         * v2节点
         * a4活动
         */
        lineNode v25 = new lineNode(1, 4, 1, null,"a4",false);
        v2.setNext(v25);
        /**
         * v3节点
         * a5活动
         */
        lineNode v35 = new lineNode(2,4, 1, null,"a5",false);
        v3.setNext(v35);
        /**
         * v4节点
         * a6活动
         */
        lineNode v46 = new lineNode(3,5, 2, null,"a6",false);
        v4.setNext(v46);
        /**
         * v5节点
         * a7活动 a8活动
         */
        lineNode v57 = new lineNode(4,6, 9, null,"a7",false);
        lineNode v58 = new lineNode(4,7, 7, null,"a8",false);
        v5.setNext(v57);
        v57.setNext(v58);
        /**
         * v6节点
         * a9活动
         */
        lineNode v68 = new lineNode(5,7, 4, null,"a9",false);
        v6.setNext(v68);
        /**
         * v7节点
         * a10活动
         */
        lineNode v79 = new lineNode(6,8, 2, null,"a10",false);
        v7.setNext(v79);
        /**
         * v8节点
         * a11活动
         */
        lineNode v89 = new lineNode(7,8, 4, null,"a11",false);
        v8.setNext(v89);
        /**
         * v10节点
         *
         */
        vertexNode v10=new vertexNode(9,null,"西安");
        /**
         * v11节点
         */
        vertexNode v11=new vertexNode(10,null,"北京");
        lineNode a13=new lineNode(8,10,6,null,"a13",false);
        lineNode a14=new lineNode(9,8,7,null,"a14",false);
        v11.setNext(a14);
        v10.setNext(a13);

        /**
         * 对象数组：vexList，保存节点构建了图
         */
        vexList = new vertexNode[11];
        vexList[0] = v1;
        vexList[1] = v2;
        vexList[2] = v3;
        vexList[3] = v4;
        vexList[4] = v5;
        vexList[5] = v6;
        vexList[6] = v7;
        vexList[7] = v8;
        vexList[8] = v9;
        vexList[9]=v10;
        vexList[10]=v11;
    }


    /**
     * 拓扑排序
     * @return true 排序成功 false 失败
     */
    public boolean topologicalSort() {
        /**
         * 计算入度：初始化所有节点的入度
         */
        for (int i=0;i<vexList.length;i++){
            vexList[i].setIn(0);
        }
        /**
         * 遍历每个节点后面的链表，然后就给弧尾顶点加一
         */
        for (int i=0;i<vexList.length;i++){
            lineNode p=new lineNode();
            p=vexList[i].getNext();
            while (p!=null){
                vertexNode vertexNode=new vertexNode();
                vertexNode=vexList[p.getAdjvex()];
                vertexNode.setIn(vertexNode.getIn()+1);
                p=p.getNext();
            }
        }

        /**
         * 计数：用来判断是否无环
         */
        int count=0;
        vertexNode p = new vertexNode();
        lineNode p1 = new lineNode();
        System.out.println("拓扑排序：");
        /**
         * 对事件最早发生时间数组初始化
         */
        etv=new int[vexList.length];
        for (int i=0;i<etv.length;i++){
            etv[i]=0;
        }
        /**
         * 将度为0的入栈
         */
        for (int i = 0; i < vexList.length; i++) {
            if (vexList[i].in == 0) {
                stack.push(vexList[i]);
            }
        }
        /**
         * 遍历领接表里面边结点，遍历到入度就减一
         */
        while (!stack .empty()) {
            p=stack.pop();
            count++;
            /**
             * 拓扑排序的逆序加入栈2中
             */
            stack1.push(p);
            System.out.print(p.getName()+" ");
            if(p.getNext()!=null){
                p1=p.getNext();
            }
            /**
             * 核心算法计算事件最早发生时间etv
             */
            while (p1!=null){
                vexList[p1.getAdjvex()].setIn(vexList[p1.getAdjvex()].getIn()-1);
                if(vexList[p1.getAdjvex()].getIn()==0){
                    stack.push(vexList[p1.getAdjvex()]);
                }
                if(etv[p.getData()]+p1.getInfo()>etv[p1.getAdjvex()]){
                    etv[p1.getAdjvex()]=etv[p.getData()]+p1.getInfo();
                }
                p1=p1.getNext();
            }
        }
        /**
         * 计数小于节点数就有回路
         * 等于就无回路
         */
        if(count!=vexList.length){
            System.out.println();
            System.out.println("图有回路！！");
            return true;
        }else {
            System.out.println();
            System.out.println("图无回路！！");
        }
        return false;
    }

    /**
     * 关键路径的方法
     */
    public void criticalPath() {
        /**
         * 活动的最早发生时间 ee
         * 活动发生的最晚时间 el
         * p 指针扫描事件节点
         * p1 扫描活动节点
         */
        int ee,el;
        vertexNode p = new vertexNode();
        lineNode p1 = new lineNode();
        /**
         * 先进行拓扑排序判断图有没有环
         */
        if (topologicalSort()){
            return;
        }
        /**
         * 初始化ltv数组
         */
         finall=stack1.peek().getData();
        ltv=new int[vexList.length];
        for (int i=0;i<vexList.length;i++){
            ltv[i]=etv[finall];
        }
        /**
         * 已经获得了拓扑排序的逆序stack2，所以对逆序求最晚发生时间
         */
        while (!stack1.empty()){
            p=stack1.pop();
            if(p.getNext()!=null){
                p1=p.getNext();
            }
            while (p1!=null){
                if (ltv[p1.getAdjvex()]-p1.getInfo()<ltv[p.getData()]){
                    ltv[p.getData()]=ltv[p1.getAdjvex()]-p1.getInfo();
                }
                p1=p1.getNext();
            }
        }

        for (int i=0;i<visited.length;i++){
            visited[i]=1;
        }
        System.out.print("关键活动为：");
        /**
         * 求ee,el和关键路径 count1表示关键活动的数量
         */
        int count1=0;
        for (int i=0;i<vexList.length;i++){
            lineNode pn=new lineNode();
            pn=vexList[i].getNext();
            while (pn!=null){
                ee=etv[i];
                el=ltv[pn.getAdjvex()]-pn.getInfo();
                if(ee==el){
                    count1++;
                   visited[vexList[i].getData()]= 0;
                    System.out.print(pn.getName()+",");
                }
                pn=pn.getNext();
            }

        }
        System.out.println();
        System.out.println("最大时间："+ltv[finall]);
           System.out.println();
    }

    /**
     * 为了输出每条关键路径用到DFS算法
     * @param k 起点再数组中的下标
     */
    public void DFS(int k){
        visited[k]=1;
        lineNode p=new lineNode();
        p=vexList[k].getNext();
        /**
         * 终点永远是关键节点
         */
        visited[finall]=0;
        /**
         * 如果走到终点遍历栈的元素
         */
        if(k==finall) {
            for (int i=0;i<stack2.size;i++) {
                System.out.print(stack2.peekTravel(i).getName() + "->");
            }
        }
        /**
         * 遍历节点后面的链表
         */
        while (p!=null){
            if(visited[p.getAdjvex()]!=1){
                /**
                 * 是关键路径就入栈
                 */
                stack2.push(p);
                DFS(p.getAdjvex());
                /**
                 * 遇见死路回退的时候出栈
                 */
                stack2.pop();
            }
            System.out.println();
            p=p.getNext();
        }
    }

    /**
     * 活动节点
     */
    class lineNode {
        /**
         * 存储该顶点对应的下标
         */
        private int adjvex;
        /**
         * 存储权值
         */
        private int info;
        /**
         * 指向下一个节点
         */
        private lineNode next;
        /**
         * 活动的名字
         */
        private String name;

        public boolean isMark() {
            return mark;
        }

        public void setMark(boolean mark) {
            this.mark = mark;
        }

        /**
         * 标识位：标识有没有遍历过
         */
        private boolean mark;

        /**
         * 弧头
         *
         */
        private int head;

        public int getHead() {
            return head;
        }

        public void setHead(int head) {
            this.head = head;
        }

        public String getName() {
            return name;
        }

        public void setName(String name) {
            this.name = name;
        }

        public lineNode(int head,int adjvex, int info, lineNode next, String name,boolean mark) {
            this.adjvex = adjvex;
            this.info = info;
            this.next = next;
            this.name=name;
            this.mark=mark;
            this.head=head;
        }
        public lineNode() {

        }

        public int getAdjvex() {
            return adjvex;
        }

        public void setAdjvex(int adjvex) {
            this.adjvex = adjvex;
        }

        public int getInfo() {
            return info;
        }

        public void setInfo(int info) {
            this.info = info;
        }

        public lineNode getNext() {
            return next;
        }

        public void setNext(lineNode next) {
            this.next = next;
        }
    }

    /**
     * 事件节点
     */
    class vertexNode {


        /**
         * 节点的名字
         */
        private String name;
        /**
         * 入度
         */
        private int in;
        /**
         * 储存顶点数组的下标
         */
        private int data;
        /**
         * 边的节点的头指针
         */

        private lineNode next;

        public int getIn() {
            return in;
        }

        public int getData() {
            return data;
        }

        public lineNode getNext() {
            return next;
        }

        public void setIn(int in) {
            this.in = in;
        }

        public void setData(int data) {
            this.data = data;
        }

        public void setNext(lineNode next) {
            this.next = next;
        }


        public vertexNode( int data, lineNode next, String name) {

            this.data = data;
            this.next = next;
            this.name = name;
        }

        public vertexNode() {

        }
        public String getName() {
            return name;
        }

        public void setName(String name) {
            this.name = name;
        }
    }
    public static void main(String[] args) {
        lessonWord a=new lessonWord();
        a.craeteGraph();
//        a.createGraph();
        a.criticalPath();
        a.DFS(0);
    }
}
栈：
package dataproject.stack;
import dataproject.importanRoad.lessonWord;
import java.util.Arrays;
/**
 * @author 李正阳  17060208112
 * @param <E> 泛型
 */
public class myArrayStack<E> {
    private int DEFAULT_SIZE = 16;//定义栈的初始默认长度
    private int capacity;//保存顺序栈的长度
    public int size;//保存顺序栈中元素的个数
    private Object[] elementData;//定义一个数组用于保存顺序栈中的元素

    public myArrayStack() {
        capacity = DEFAULT_SIZE;
        elementData = new Object[capacity];
    }

    //以指定的大小来创建栈
    public myArrayStack(int initSize){
        capacity = 1;
        while(capacity < initSize) {
            capacity <<= 1;//将capacity设置成大于initSize的最小2次方
            elementData = new Object[capacity];
        }
    }

    //返回当前顺序栈中元素的个数
    public int length() {
        return size;
    }

    public E pop() {
        if(empty()) {
            throw new IndexOutOfBoundsException("栈空，不能出栈");
        }
        E oldValue = (E)elementData[size - 1];
        elementData[--size] = null;//让垃圾回收器及时回收，避免内存泄露
        return oldValue;
    }

    public void push(E element) {
        ensureCapacity(size + 1);
        elementData[size++] = element;
    }


    private void ensureCapacity(int minCapacity){
        if(minCapacity > capacity){
            while(capacity < minCapacity) {
                capacity <<= 1;
                elementData = Arrays.copyOf(elementData, capacity);
            }
        }
    }

    //获取栈顶元素，不会将栈顶元素删除
    public E peek() {
        if(size == 0) {
            throw new ArrayIndexOutOfBoundsException("栈为空");
        }
        return (E)elementData[size - 1];
    }

    /**
     * @param d 这个元素的位置
     * @return 返回d所处的元素
     */
    public E peekTravel(int d) {
        if(size == 0) {
            throw new ArrayIndexOutOfBoundsException("栈为空");
        }
        return (E)elementData[d];
    }
    public boolean empty() {
        return size == 0;
    }
    public void clear() {
        for(int i = 0; i < size; i++) {
            elementData[i] = null;
        }
        size = 0;
    }

    public static void main(String[] args) {

    }

}

流程图：