考场上面做了一个暴力的做法,然后,然后他$WA$了。
emmm...($T$就算了吧,$WA$了算什么事啊)
好吧,这道题,其实好像...是一道思维题来着。
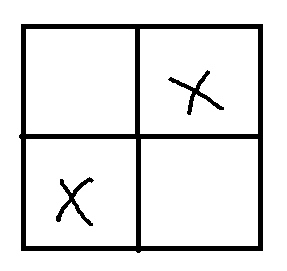
如果出现了这样两个打X的格子上的字符相同,那么全局则一定有两条以上的字符串一样的路。因为从(1,1)有一条路到左上角,左上角到右下角分别经过两个打X的格子到右下角,最后再从右下角随便找一条路到(n,m)就可以了。
简单证明一下如果没有出现这种情况,一定不会有两条不同的路符合条件。假设已经走到了某一个点,因为只能往右或者往下走,如果那两个位置不一样,形成的字符串就一定会是不一样的。
简单实现的话,直接判断有没有这种情况出现就好了。但是和大佬学习了一下,用了一个递推(类似dp?)的做法。

1 #include<iostream> 2 #include<string> 3 #include<cstdio> 4 #include<cstring> 5 #include<map> 6 #include<algorithm> 7 using namespace std; 8 #define N 1005 9 #define ll long long 10 int n,m; 11 char mp[N][N]; 12 int f[N][N];//f[i][j]01状态表示(i,j)能否有2种及以上的方法到达 13 int main() 14 { 15 int T;scanf("%d",&T); 16 while(T--) 17 { 18 memset(f,0,sizeof(f)); 19 scanf("%d %d",&n,&m); 20 for(int i=1;i<=n;i++) 21 scanf("%s",mp[i]+1); 22 for(int i=1;i<=n;i++) 23 for(int j=1;j<=m;j++) 24 { 25 26 f[i][j]|=f[i-1][j]|f[i][j-1]; 27 //如果到这两个格子有两种及以上走法,那么到这一个格子也肯定有 28 if(i>1&&j>1) 29 f[i][j]|=(mp[i-1][j]==mp[i][j-1]); 30 //如果这两个格子一样,那么可以从(i-1,j-1)走到这两个格子,再走到(i,j),有2种走法 31 } 32 if(f[n][m]) puts("Yes"); 33 else puts("No"); 34 } 35 return 0; 36 }
