学习内容:本周的话主要讲了三相异步电机和它的启动、调速、制动的方法。重点的话定子旋转磁场方向等判断,异步电机的人为机械特性分析。对这部分理解还不够深。课下又看了几遍,才敢做以下仿真。
仿真:
本次仿真任务如下:
1)实现如下机械运动周期:
控制电机带重物上升,从静止加速到800r/min
保持800r/min匀速运动0.5s,
减速到静止,保持静止状态0.5s,
带重物下降,从静止达到600r/min
保持600r/min匀速运动0.6s,
减速到静止。
(为了便于仿真,匀速和静止持续时间较短)
本次控制策略选择:
首先,经过长时间参数试验,得知一般的控制规律,再结合课本,开始进行控制。首先对这几段运动,按所需的评价指标修改,对于第一段启动,采用便捷的定子串电阻方法,可以降低冲击转矩和冲击电流,而启动时间的控制,便是常规处理计算频率,调频即可,另外用到电压调节,即用变频,变电压结合方法,以下均是该方法。 对于第一次制动,我们可以选择几个相对较低的频率降低制动时间,同时减小电压倍数来降低冲击转矩。以下几个启动制动过程均是该思想,经过反复试验,调节参数,找规律,可以拟合出电机带动重物升降的过程Tm,n的变化。
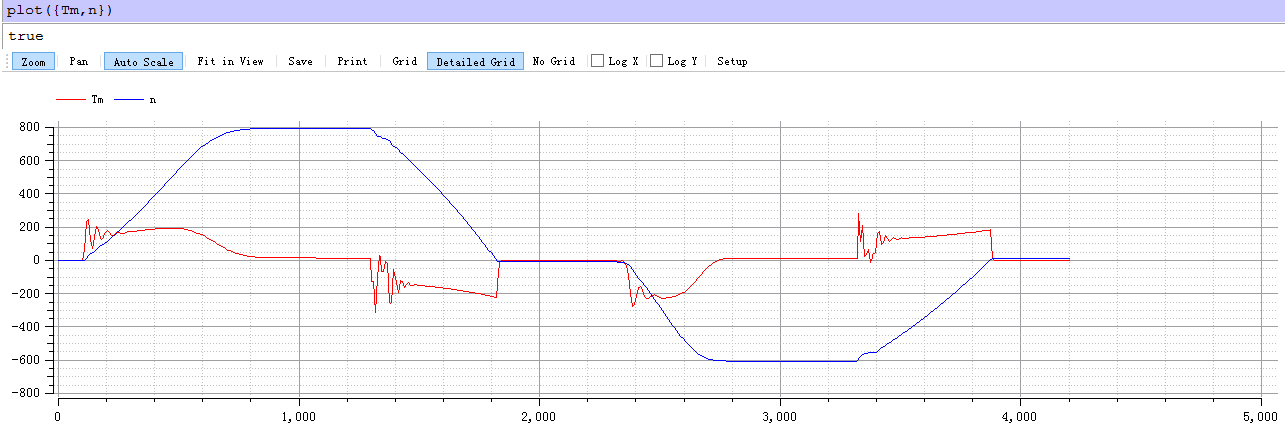
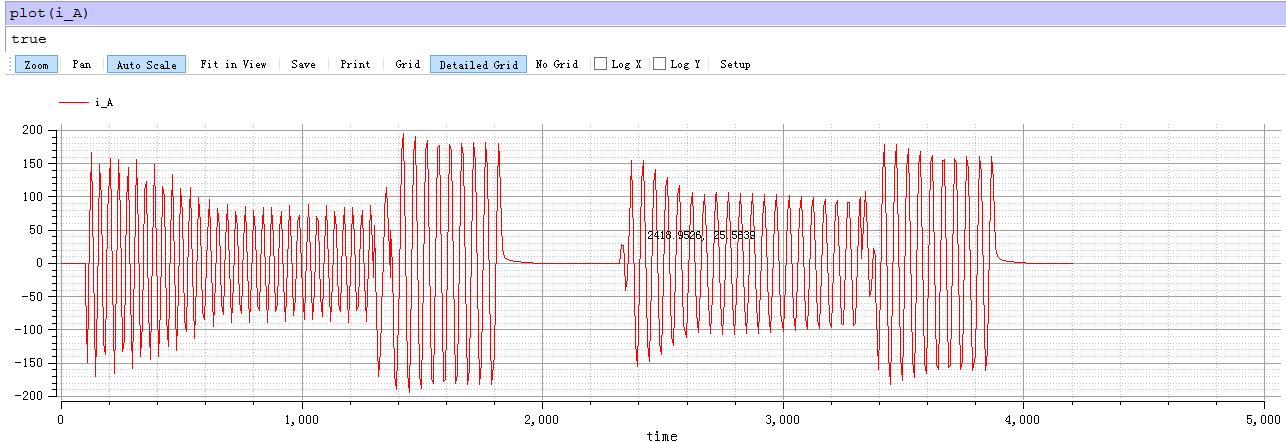
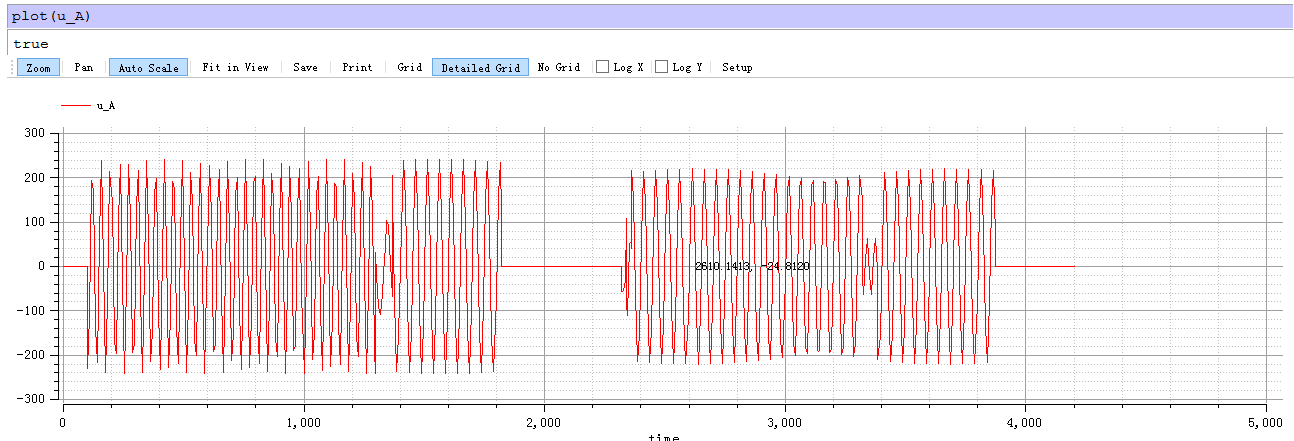
编写程序如下:
model SACIM "A Simple AC Induction Motor Model"
type Voltage=Real(unit="V");
type Current=Real(unit="A");
type Resistance=Real(unit="Ohm");
type Inductance=Real(unit="H");
type Speed=Real(unit="r/min");
type Torque=Real(unit="N.m");
type Inertia=Real(unit="kg.m^2");
type Frequency=Real(unit="Hz");
type Flux=Real(unit="Wb");
type Angle=Real(unit="rad");
type AngularVelocity=Real(unit="rad/s");
constant Real Pi = 3.1415926;
Current i_A"A Phase Current of Stator";
Current i_B"B Phase Current of Stator";
Current i_C"C Phase Current of Stator";
Voltage u_A"A Phase Voltage of Stator";
Voltage u_B"B Phase Voltage of Stator";
Voltage u_C"C Phase Voltage of Stator";
Current i_a"A Phase Current of Rotor";
Current i_b"B Phase Current of Rotor";
Current i_c"C Phase Current of Rotor";
Frequency f_s"Frequency of Stator";
Torque Tm"Torque of the Motor";
Speed n"Speed of the Motor";
Flux Psi_A"A Phase Flux-Linkage of Stator";
Flux Psi_B"B Phase Flux-Linkage of Stator";
Flux Psi_C"C Phase Flux-Linkage of Stator";
Flux Psi_a"a Phase Flux-Linkage of Rotor";
Flux Psi_b"b Phase Flux-Linkage of Rotor";
Flux Psi_c"c Phase Flux-Linkage of Rotor";
Angle phi"Electrical Angle of Rotor";
Angle phi_m"Mechnical Angle of Rotor";
AngularVelocity w"Angular Velocity of Rotor";
Torque Tl"Load Torque";
parameter Resistance Rs = 0.531"Stator Resistance";
parameter Resistance Rr = 0.408"Rotor Resistance";
parameter Inductance Ls = 0.00252"Stator Leakage Inductance";
parameter Inductance Lr = 0.00252"Rotor Leakage Inductance";
parameter Inductance Lm = 0.00847"Mutual Inductance";
parameter Frequency f_N = 26.77778 "Rated Frequency of Stator";
parameter Voltage u_N = 220"Rated Phase Voltage of Stator";
parameter Real p =2"number of pole pairs";
parameter Inertia Jm = 0.1"Motor Inertia";
parameter Inertia Jl = 1 "Load Inertia";
parameter Resistance R0 = 0.331"exception Resistance";
initial equation
Psi_A = 0;
Psi_B = 0;
Psi_C = 0;
Psi_a = 0;
Psi_b = 0;
Psi_c = 0;
phi = 0;
w = 0;
equation
u_A = (Rs+R0) * i_A + 1000 * der(Psi_A);
u_B = (Rs+R0) * i_B + 1000 * der(Psi_B);
u_C = (Rs+R0) * i_C + 1000 * der(Psi_C);
0 = Rr * i_a + 1000 * der(Psi_a);
0 = Rr * i_b + 1000 * der(Psi_b);
0 = Rr * i_c + 1000 * der(Psi_c);
Psi_A = (Lm+Ls)*i_A + (-0.5*Lm)*i_B + (-0.5*Lm)*i_C + (Lm*cos(phi))*i_a + (Lm*cos(phi+2*Pi/3))*i_b + (Lm*cos(phi-2*Pi/3))*i_c;
Psi_B = (-0.5*Lm)*i_A + (Lm+Ls)*i_B + (-0.5*Lm)*i_C + (Lm*cos(phi-2*Pi/3))*i_a + (Lm*cos(phi))*i_b + (Lm*cos(phi+2*Pi/3))*i_c;
Psi_C = (-0.5*Lm)*i_A + (-0.5*Lm)*i_B + (Lm+Ls)*i_C + (Lm*cos(phi+2*Pi/3))*i_a + (Lm*cos(phi-2*Pi/3))*i_b + (Lm*cos(phi))*i_c;
Psi_a = (Lm*cos(phi))*i_A + (Lm*cos(phi-2*Pi/3))*i_B + (Lm*cos(phi+2*Pi/3))*i_C + (Lm+Lr)*i_a + (-0.5*Lm)*i_b + (-0.5*Lm)*i_c;
Psi_b = (Lm*cos(phi+2*Pi/3))*i_A + (Lm*cos(phi))*i_B + (Lm*cos(phi-2*Pi/3))*i_C + (-0.5*Lm)*i_a + (Lm+Lr)*i_b + (-0.5*Lm)*i_c;
Psi_c = (Lm*cos(phi-2*Pi/3))*i_A + (Lm*cos(phi+2*Pi/3))*i_B + (Lm*cos(phi))*i_C + (-0.5*Lm)*i_a + (-0.5*Lm)*i_b + (Lm+Lr)*i_c;
Tm =-p*Lm*((i_A*i_a+i_B*i_b+i_C*i_c)*sin(phi)+(i_A*i_b+i_B*i_c+i_C*i_a)*sin(phi+2*Pi/3)+(i_A*i_c+i_B*i_a+i_C*i_b)*sin(phi-2*Pi/3));
w = 1000 * der(phi_m);
phi_m = phi/p;
n= w*60/(2*Pi);
Tm-Tl = (Jm+Jl) * 1000 * der(w);
if time <= 100 then
u_A = 0;
u_B = 0;
u_C = 0;
f_s = 0;
Tl = 0;
elseif time <= 797 then
f_s = f_N;
u_A = u_N * 1.100 * sin(2*Pi*f_s*time/1000);
u_B = u_N * 1.100 * sin(2*Pi*f_s*time/1000-2*Pi/3);
u_C = u_N * 1.100 * sin(2*Pi*f_s*time/1000-4*Pi/3);
Tl = 15;
elseif time <= 1297 then
f_s = f_N;
u_A = u_N * 1.100 * sin(2*Pi*f_s*time/1000);
u_B = u_N * 1.100 * sin(2*Pi*f_s*time/1000-2*Pi/3);
u_C = u_N * 1.100 * sin(2*Pi*f_s*time/1000-4*Pi/3);
Tl = 15;
elseif time <= 1337 then
f_s = 15;
u_A = u_N * 0.5 * sin(2*Pi*f_s*time/1000);
u_B = u_N * 0.5 * sin(2*Pi*f_s*time/1000-4*Pi/3);
u_C = u_N * 0.5 * sin(2*Pi*f_s*time/1000-2*Pi/3);
Tl = 15;
elseif time <=1367 then
f_s = 18;
u_A = u_N * 0.5 * sin(2*Pi*f_s*time/1000);
u_B = u_N * 0.5 * sin(2*Pi*f_s*time/1000-4*Pi/3);
u_C = u_N * 0.5 * sin(2*Pi*f_s*time/1000-2*Pi/3);
Tl = 15;
elseif time <=1821 then
f_s = 20;
u_A = u_N * 1.100 * sin(2*Pi*f_s*time/1000);
u_B = u_N * 1.100 * sin(2*Pi*f_s*time/1000-4*Pi/3);
u_C = u_N * 1.100 * sin(2*Pi*f_s*time/1000-2*Pi/3);
Tl = 15;
elseif time <=2321 then
u_A = 0;
u_B = 0;
u_C = 0;
f_s = 0;
Tl = 0;
elseif time <= 2341 then
f_s=115;
u_A = u_N * 0.5 * sin(2*Pi*f_s*time/1000);
u_B = u_N * 0.5 * sin(2*Pi*f_s*time/1000-4*Pi/3);
u_C = u_N * 0.5 * sin(2*Pi*f_s*time/1000-2*Pi/3);
Tl = 15;
elseif time <= 2361 then
f_s=40;
u_A = u_N * 0.5 * sin(2*Pi*f_s*time/1000);
u_B = u_N * 0.5 * sin(2*Pi*f_s*time/1000-4*Pi/3);
u_C = u_N * 0.5 * sin(2*Pi*f_s*time/1000-2*Pi/3);
Tl = 15;
elseif time <= 2719 then
f_s=20;
u_A = u_N * 1.0 * sin(2*Pi*f_s*time/1000);
u_B = u_N * 1.0 * sin(2*Pi*f_s*time/1000-4*Pi/3);
u_C = u_N * 1.0 * sin(2*Pi*f_s*time/1000-2*Pi/3);
Tl = 15;
elseif time <= 3319 then
f_s = 20;
u_A = u_N * 1.0 * sin(2*Pi*f_s*time/1000);
u_B = u_N * 1.0 * sin(2*Pi*f_s*time/1000-4*Pi/3);
u_C = u_N * 1.0 * sin(2*Pi*f_s*time/1000-2*Pi/3);
Tl = 15;
elseif time <=3384 then
f_s = 30;
u_A = u_N * 0.3 * sin(2*Pi*f_s*time/1000);
u_B = u_N * 0.3 * sin(2*Pi*f_s*time/1000-2*Pi/3);
u_C = u_N * 0.3 * sin(2*Pi*f_s*time/1000-4*Pi/3);
Tl = 15;
elseif time <=3873 then
f_s = 20;
u_A = u_N * 1.0 * sin(2*Pi*f_s*time/1000);
u_B = u_N * 1.0 * sin(2*Pi*f_s*time/1000-2*Pi/3);
u_C = u_N * 1.0 * sin(2*Pi*f_s*time/1000-4*Pi/3);
Tl = 15;
else
u_A = 0;
u_B = 0;
u_C = 0;
f_s = 0;
Tl = 0;
end if;
end SACIM;