【线性表6】线性表的链式实现：双向链表

简介

在单链表中，我们只能向一个方向（向后）访问结点：即从索引小的到索引大的方向，而不能逆向访问，例如通过第3个结点的指针，无法直接得到第2个结点的地址。这是因为单链表的每一个结点只保存了下一个结点的地址。

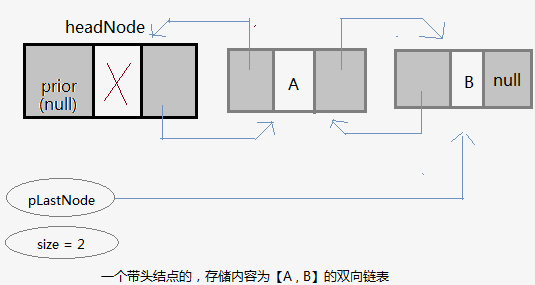
而双向链表中，结点有2个指针域：prior 和 next。next同样保存下一个结点的指针，而结点新增的成员prior则用来保存前一个结点的地址。

 

因此，双向链表在访问元素操作上比单链表快。为什么？例如，链表总长度为100，在单链表中，要访问索引为第98的结点（倒数第二个），我们必须从索引为0的结点开始向后迭代寻。而在双向链表中，我们先通过逻辑判断：索引为98的结点，是更靠近首结点（索引为0），还是更靠近尾结点（索引为99）？这里当然是更靠近尾结点，则从尾结点开始向前迭代。

对于双向链表，他的缺点也很明显：

1、比单链表更占空间，因为每个结点多了一个指针域。

2、操作复杂。

但这不影响它的使用，从实际应用的角度看，他的优点大于他的缺点。例如在Java集合框架中，LinkedList就是一个双向链表。

结点的定义

struct DLNode    //双向链表的结点定义
{
    int element;      //数据域
    DLNode* prior     //指针域：保存前一个结点的指针
    DLNode* next;     //指针域：保存后一个结点的指针
    
    ListNode(int e=0,DLNode* pri=0,DLNode* nxt = 0):element(e),prior(pri),next(nxt)
    {
    }
    
};

代码实现

初始化状态

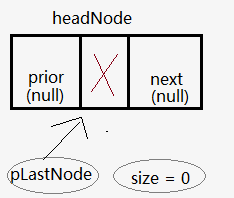
#include<iostream>
#include<cstdlib>
#include<stdexcept>
using namespace std;
struct DLNode    //双向链表的结点定义
{
    int element;      //数据域
    DLNode* prior;     //指针域：保存前一个结点的指针
    DLNode* next;     //指针域：保存后一个结点的指针
    
    DLNode(int e=0,DLNode* pri=0,DLNode* nxt = 0):element(e),prior(pri),next(nxt)
    {
    }
    
};
class DLinkList
{
private:
    DLNode   headNode;    //头结点
    DLNode * pLastNode;   //尾结点指针
    int size;             //长度
    //获取双向链表中，索引为index 的结点的地址。
    //如果不存在此结点，则返回NULL
    DLNode* _getNodeAt(int index) const
    {
        DLNode*p;
        int i;
        
        if(index < 0 || index >=size ) return 0;   //返回NULL
        
        
        if( index  < size /2) //从前向后寻找更快到达
        {
        
            for(i=0,p=headNode.next    ;  i<index ;i++,p=p->next){
                // NOOP
            }
            return p;
        }
        else
        {
            //从后向前 寻找更快到达
            for(i=size-1,p = pLastNode; i>index ;i--,p=p->prior){
                // NOOP
            }
            return p;
        }
        
    }
public:
    DLinkList():headNode(),pLastNode(&headNode),size(0)
    {    
    
        /*
        *
        *             *************************
        *             *        *      *       *
        *             * prior  *   x  * next  *
        *             * (NULL) *      *(NULL) *
        *             *************************
        *                 /     headNode
        *                 /   
        *                /
        *               /
        *             pLastNode = &headNode
        *
        *             size = 0
        *
        ********/
    }
    
    ~DLinkList()
    {
        clear();
    }
    
    //追加一个元素到表末尾
    void append(int e)
    {
        DLNode * new_node  = new DLNode(e,pLastNode,0);   //新结点向前连接
        
        pLastNode->next = new_node;    //最后一个结点向后连接新的尾结点
            
        pLastNode = new_node;        //更新最后一个结点指针
        
        size++;
    }
    
    bool insert(int index,int e)
    {
        
        DLNode*new_node;
        DLNode*p  = _getNodeAt(index-1);  //获取待插入位置的前一个结点地址
        if(p==0) return false;
        
        new_node = new DLNode(e,p,p->next);
        
        if(p->next ==0)
            pLastNode = new_node;  //如果新结点是插入为最后一个结点，则更新pLastNode的值
        else
            p->next->prior = new_node;
    
        p->next = new_node;
        size++;
        return true;
    }
    
    bool remove(int index)
    {
        DLNode*del_node;
        DLNode*p  = _getNodeAt(index-1);  //获取待删除结点的前一个结点地址     
        if(p==0 || p->next ==0) return false;
        
        
        del_node = p->next;
        
        p->next = p->next->next;
        
        if(p->next->next == 0){    //说明被删除的是最后一个结点
            pLastNode = p;
        }else{
            p->next->next->prior = p;
        }
        
        delete del_node;
        size--;
        return true;
        
    }
    
    
    size_t length ()const
    {
        return size;
    }
    
    bool isEmpty()const
    {
        return size == 0;
    }
    
    int indexOf(int e) const
    {
        DLNode *p = headNode.next;
        int i=0;
        while(p!=0){
            if(p->element == e) return i;
            i++;
            p=p->next;
        
        }
        return -1;
    }
    
    /*
    * 功能：删除所有的数据结点，清空表
    */
    void clear()
    {
        
        DLNode*p =  headNode.next;
        DLNode*t;
        while(p!=0){
        
            t = p;
            p=p->next;
            delete t;
        }
        
        //回归初始状态
        headNode.next = 0;
        pLastNode = &headNode;
        size = 0;
    }
    
    
    
    void show()const
    {
        DLNode*p =  headNode.next;
        cout<<'[';
        while(p!=0)
        {
            if(p!=headNode.next)
                cout<<',';
            cout<<p->element;
            p = p->next;
        }
        cout<<']';
    }
    
    
    int operator[](int index) const
    {
        DLNode*p = _getNodeAt(index);
        if(p==0)
            throw std::out_of_range(0);
        
        return p->element;         
        
    }
    
    int& operator[](int index)
    {
        DLNode*p = _getNodeAt(index);
        
        if(p==0)
            throw std::out_of_range(0);
        return p->element;    
    }
    
};
int main()
{
    
    
    DLinkList list;
    
    for(int i=0;i<10;++i)
        list.append(i);
    list.show(); cout<<'
';
    
    
    list.remove(3);
    list.remove(3);
    list[0] = 101;
    list.show(); cout<<'
';
    
    return 0;
}

总结

单链表 vs 双向链表：双向链表由于结点多了一个指针域，因此空间占用量比单链表高，但是结点的访问时间却可以加快了，因为我们可以选择最近的迭代查找方向，从尾结点向前，或者从头结点向后。这是一个用空间换时间的例子。实际开发中，双向链表更加通用，强大。

DLNode* _getNodeAt(int index) const
{
        DLNode*p;
        int i;
        if(index < 0 || index >=size ) return 0;   //索引不合法，返回NULL
        
        if( index  < size /2) //从前向后寻找更快到达
        {
            for(i=0,p=headNode.next    ;  i<index ;i++,p=p->next){
                // NOOP
            }
            return p;
        }
        else
        {
            //从后向前 寻找更快到达
            for(i=size-1,p = pLastNode; i>index ;i--,p=p->prior){
                // NOOP
            }
            return p;
        }
        
}