郑重声明：原文参见标题，如有侵权，请联系作者，将会撤销发布！
Preprint · September 2020
Abstract
脉冲神经网络(SNN)具有在专用神经形态硬件上高效实现深度神经网络(DNN)的巨大潜力。最近的研究表明，在图像分类任务(包括CIFAR10和ImageNet数据)上，与DNN相比，SNN具有竞争优势。目前的工作着重于结合SNN与ATARI游戏中的深度强化学习，与图像分类相比，它涉及更多的复杂性。我们回顾了将DNN转换为SNN并将转换扩展到深度Q网络(DQN)的理论。我们提出了发放率的可靠表征，以减少转换过程中的误差。此外，我们引入了一种新的指标来评估转换过程，方法是分别比较DQN和SNN做出的决策。我们还分析了仿真时间和参数归一化如何影响转换后的SNN的性能。我们在17项性能最优的Atari游戏中获得了相当的得分。据我们所知，我们的工作是第一个在具有SNN的多个Atari游戏上实现最新性能的工作。我们的工作为将DQN转换为SNN提供了基准，并为进一步研究解决SNN强化学习任务铺平了道路。
Introduction
近年来，深度卷积神经网络(CNN)在图像识别方面取得了巨大成功(LeCun, Bengio, and Hinton, 2015; He et al., 2016)。经过深度RL训练的CNN在许多RL任务中的表现甚至达到甚至超过了人类水平(Mnih et al., 2015; Vinyals et al., 2019)。但是，结合DNN进行深度RL需要大量资源，在某些实际问题中可能无法获得。例如，在许多现实生活场景中，要求处理系统具有高能效和低延迟(Cheng et al., 2016)。
脉冲神经网络(SNN)提供了一种有吸引力的解决方案，可以减少延迟和计算负荷。与处理连续激活值的ANN相反，SNN使用脉冲通过许多离散事件传输信息。这使SNN更加节能。SNN可以在专用硬件上实现，例如IBM的TrueNorth (Merolla et al., 2014)和英特尔的Loihi (Davies et al., 2018)。据报道，它们的能源效率是传统芯片的1000倍。因此，随着ANN在社会许多领域的应用，SNN有潜力满足对AI的快速增长的需求。
理论分析表明，SNN在计算上与常规神经元模型一样强大(Maass and Markram, 2004)，但是，目前SNN的使用非常有限。主要原因是训练多层SNN是一个挑战，因为SNN的激活函数通常是不可微的。因此，与ANN相反，不能使用基于梯度下降的方法来训练神经网络。训练SNN的方法有多种，例如使用随机梯度下降法(O'Connor and Welling, 2016)，将膜电位可微化(Lee, Delbruck, and Pfeiffer, 2016)，事件驱动的随机反向传播(Neftci et al., 2017)和其他方法(Tavanaei and Maida, 2019; Kheradpisheh et al., 2018; Mozafari et al., 2018)。与ANN相比，这些方法在浅层网络的MNIST (LeCun et al., 1998)上具有竞争优势。但是，它们在更现实和复杂的数据集上的性能都没有竞争力，例如CIFAR-10 (Krizhevsky, Sutskever and Hinton, 2012)和ImageNet (Russakovsky et al., 2015)。最近，(Wu et al., 2019)和(Lee et al., 2020)使用基于脉冲的反向传播在CIFAR-10上实现了90％以上的精度，这对于直接训练SNN而言是一个巨大的进步。
为了避免训练SNN的困难，同时利用SNN处理的优势，我们遵循(Pérez-Carrasco et al., 2013)提出的将ANN转换为SNN的替代方法。该方法采用预训练ANN的参数，并将它们映射到具有相同架构的等效SNN (Diehl et al., 2015) (Rueckauer et al., 2017) (Sengupta et al., 2019)。由于ANN具有许多高性能的训练方法，因此我们的目标是将最先进的ANN直接转换为神经网络，而不会降低性能。(Sengupta et al., 2019)的最新工作表明这种转换的确是可能的。也就是说，他们表明，即使非常深的ANN，如VGG16和ResNet，也可以成功转换为SNN，而CIFAR-10和ImageNet数据集的错误率不到1％。
继ANN到SNN转换方法在图像分类任务上取得成功之后，希望扩展这些结果以解决深度RL问题。然而，事实证明，使用深度SNN解决RL任务非常困难。问题可以总结如下。由于针对训练好的ANN进行图像分类的优化过程中使用的误差性质，正确类别的得分始终明显高于其他类别。因此，转换过程的误差不会对最终性能产生重大影响。但是，对于深度Q网络(DQN)，即使对于训练好的网络，不同动作的输出q值也通常非常相似。这使得网络更容易受到转换过程中引入的误差的影响。这是将DQN转换为SNN的艰巨任务的关键原因。
在本文中，我们提出了SNN来解决深度RL问题。与(Rueckauer et al., 2017)提出的等效模拟激活值相比，我们的方法提供了脉冲神经元发放率的更准确近似值。首先，我们探索和解释(Rueckauer et al., 2017)描述的参数归一化的效果。接下来，我们通过在仿真时间结束时使用膜电压来减少转换过程中引起的误差，从而提出了更为可靠的发放率表征。最后，我们在17种Atari游戏中测试了所提出的将DQN转换为SNN的方法。它们都达到了与原始DQN相当的性能。这项工作探讨了在深度RL领域中采用SNN的可行性。成功的实现将促进SNN在未来的各种机器学习任务中的使用。
Related work
为了开发一种有效的方法来处理从事件驱动的传感器收集的数据，(Pérez-Carrasco et al., 2013)通过在卷积网络和SNN之间映射权重参数，将传统的帧驱动的卷积网络转换为事件驱动的SNN。但是，此方法需要调整表征各个神经元动态的参数。此外，它遭受相当大的精度损失。随着CNN的成功，研究人员开始致力于使用SNN解决计算机视觉问题，尤其是在使用转换方法进行图像分类和对象识别方面。(Cao, Chen, and Khosla, 2015)率先报道了CIFAR-10的高精度，其中SNN由CNN转换而成。它使用ReLU来确保所有激活值都是非负的，并且简单的IF脉冲神经元消除了调整额外参数的需要。下一节将对IF神经元模型进行描述。他们的方法有多个简化。例如，它需要在每次训练迭代后将所有偏差都设置为零，并且它使用空间线性子采样而不是更流行的最大池化。
基于(Cao, Chen, and Khosla, 2015), (Diehl et al., 2015)提出了一种新的权重归一化方法，以实现ANN的激活值和SNN的发放率在相同范围内。他们报告了MNIST的测试精度为99.1％。Rueckauer et al. (2017)提出了转换方法的综合数学理论。他们将脉冲神经元发放率的近似值等同于等效的模拟激活值。脉冲神经元产生脉冲后，他们的方法从膜电位中减去神经元的阈值，而不是将膜电位复位为零。他们观察到这种方法可以减少误差。此外，他们基于(Diehl et al., 2015)，以缓解较高层的低发放率。他们还提供了将ANN中的许多常见操作转换为其等效SNN版本的方法，例如最大池化，softmax，批正则化和Inception模块。通过这些方法，一些深度神经网络架构(例如VGG-16和Inception-v3)已成功转换为SNN。他们报告了MNIST，CIFAR-10和ImageNet的良好性能。
(Sengupta et al., 2019)提出了一种新方法来根据输入数据调整阈值，而不是进行权重归一化。他们成功地将ResNet转换为SNN。他们的工作实现了CIFAR-10和ImageNet上转换方法的最新技术。(Rueckauer and Liu, 2018)提出了使用首次脉冲时间代替发放率来表示ANN的激活值。尽管此方法大大减少了计算量，但会引入更多误差。与基于发放率的转换方法相比，该方法报告在MNIST上的测试精度损失约为1％，该损失将在更复杂的数据集和任务中放大。
各种研究旨在将转换方法应用于其他任务以利用SNN，例如基于事件的视觉识别(Ruckucker et al., 2019)和自然语言处理(NLP) (Diehl et al., 2016)。(Patel et al., 2019)首次尝试使用SNN进行深度RL任务。它使用粒子群优化(PSO)搜索最优的权重缩放参数。尽管此方法的性能接近使用浅层网络的DQN，并且具有更高的抗干扰性，但由于探索空间大，因此在深度DQN网络上失败。
Methods
在本节中，我们首先提供转换方法的数学框架，将工作扩展为(Rueckauer et al., 2017)。基于发展的理论，我们提出了两种方法来减少误差并提高SNN中的发放率。
Theory for converting ANNs to SNNs
转换方法的主要思想是建立SNN的发放率与ANN的激活值之间的关系。通过这种关系，我们可以将训练好的ANN权重映射到SNN，这样就可以直接获得高性能的SNN，而无需额外的训练。(Rueckauer et al., 2017)综述了最新技术，并提出了完整的数学理论，该理论涉及如何使脉冲神经元的发放率近似于等效的模拟激活值。他们的推导有些过分简化，可能导致转换过程中的误差。在这项工作中，我们纠正了这些误差，并使数学结果更加可靠。仅当脉冲神经元的选定阈值不是一个阈值时，本工作中引入的校正才重要。
我们使用的脉冲神经元是IF神经元，它是最简单的脉冲神经元模型之一。IF神经元简单地对其输入进行积分，直到膜电位超过电压阈值并产生脉冲为止。IF神经元没有衰减机制，我们假设没有不应期，这与人工神经元更为相似。
对于具有L层的SNN，让Wl, bl, l ∈ {1, ... , L}表示第 l 层的权重和偏差。层 l 在时间 t 的输入电流zl(t)可计算为：
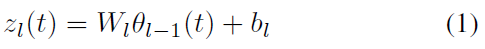
其中θl-1(t)是一个矩阵，表示层l-1中的神经元是否在时间 t 产生脉冲：
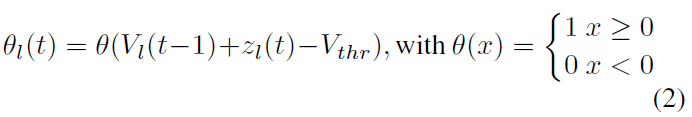
其中Vl(t-1)表示在时间t-1处 l 层中脉冲神经元的膜电位。Vthr是脉冲神经元的阈值。
在此，我们的公式(1)与(Rueckauer et al., 2017)中的公式稍有不同，后者的公式为zl(t) = Vthr(Wlθl-1(t)+ bl)。如果所有输入电流都乘以阈值，则等于将阈值设置为1。然后得出的结果是，无论我们设置的阈值如何，输入电流都会改变相应的倍数，从而抵消了阈值的影响。
通常，典型的IF神经元在产生脉冲后会将其膜电位复位为零。但是，缺少电压超过阈值的消息。(Rueckauer et al., 2017)证明它将引入新的错误并提出解决方案。当神经元的膜电位超过阈值时，而不是将其重置为零，而是从膜电位中减去阈值的电压。在这项工作中，我们还对IF神经元采用了这种减法机制：
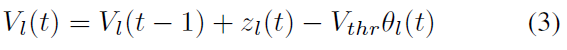
公式(1)和(3)说明了IF神经元的主要机制。基于这两个公式，我们将尝试建立SNN的发放率与ANN的激活值之间的关系。
当l > 0时，通过在仿真时间 t 上累积公式(3)，我们可以得出以下结论：
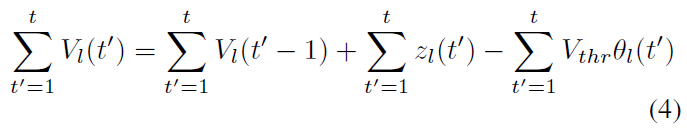
将公式(1)插入公式(4)，然后将整个公式除以 t，我们可以得出以下结论：
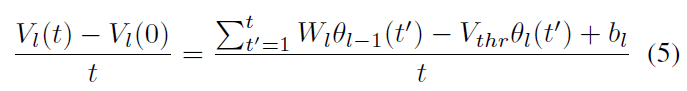
其中Vl(0) = 0，
，它是层 l 在时间 t 的发放率。为简单起见，时间步骤设置为1个单位，因此
。公式(5)可简化为：
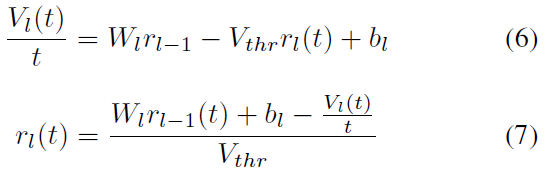
令
为
。这导致：
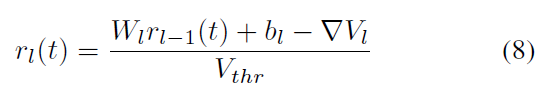
该公式是核心公式，它描述了相邻层之间发放率的关系。与ANN相似，第 l 层的发放率主要由权重乘以前一层l-1的发放率与偏差之和得出。但是，在仿真时间结束时，发放率还应减去由于遗漏剩余膜电压携带的信息而导致的近似误差。此外，很明显，发放率与阈值成反比。
当l = 0时，层0为输入层。为了将SNN的发放率与ANN的激活值相关联，我们使它们具有相同的输入，即z0 = a0，其中a0是ANN的输入值。注意a0缩放为[0, 1](与z0具有相同的范围)，可以在训练ANN之前或之后进行。它产生：
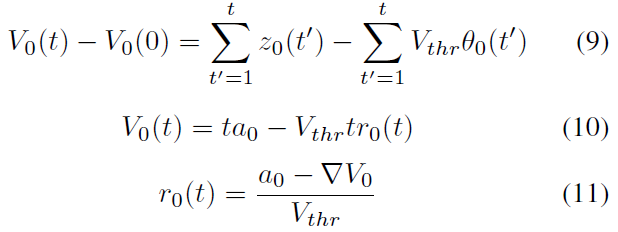
通过从第一层公式(11)重复向上一层插入公式(8)，我们得出以下结论：
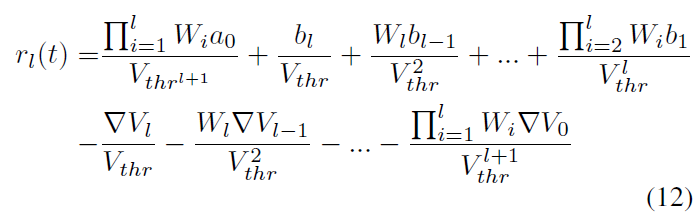
然而，(Rueckauer et al., 2017)提出的最终公式为：
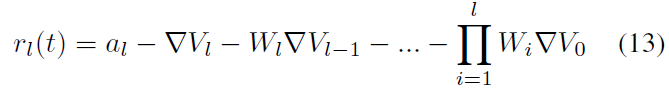
其中al是第 l 层中ANN的激活值。如上所述，在该工作中，阈值被不必要地增加。因此，如果我们在公式(12)中将Vthr设置为1，这也是我们在实验中所做的，公式(12)和(13)将非常相似。这产生：
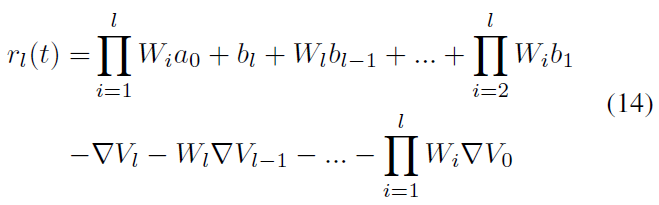尽管两个公式具有相同的误差部分，但权重和偏差部分不同。(Rueckauer et al., 2017)忽略了激活函数：
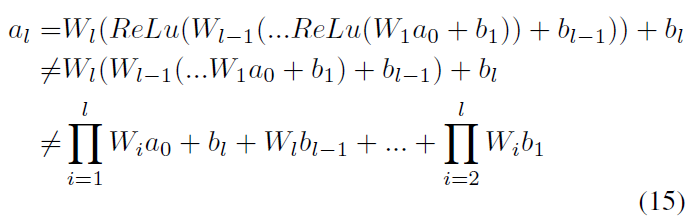
因此，实际上，SNN的发放率与ANN的激活值之间没有直接关系。发放率不能简单地表示为ANN的激活值和某些误差项的总和。但是，尽管没有激活函数，但发放率绝对是ANN激活值的估计。让我们回到公式(8)。尽管它并未明确应用ReLU，但它确实包含ReLU机制。因为脉冲神经元只能在一个时间步骤产生一个脉冲，所以
。并且
。发放率的范围是[0, 1]。它保证下一层的所有输入都大于或等于0，这与ReLU具有相同的效果。
公式(8)的误差项
是仿真时间结束时保留在神经元中的膜电位，它取决于上一层的总输入电流Wlrl-1(t)+ bl。值得注意的是，如果脉冲神经元接受负电流，则膜电位可能为负。因此，公式(8)有四种情况。为简单起见，令
。
。这是最常见的情况之一。脉冲神经元接收正电流并保持正膜电位，该电位小于阈值。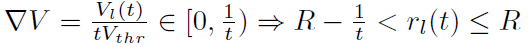
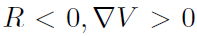。这是唯一不可能的情况。如果总电流为负，则剩余的膜电位不能为正。
。尽管总电流为正，但在最终脉冲之后的仿真时间结束之前，脉冲神经元开始接收负电流，这使得最终膜电位为负。就像神经元产生了脉冲的透支一样。与ANN不同，由于输入脉冲的顺序不同，发放率可能与输入的发放率不同。在这种情况下，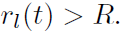
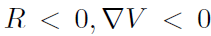。这种情况也很常见。最常见的示例之一是，脉冲神经元在仿真时间内继续接收负电流并且不产生脉冲。因此，下一层的总输入为0。这就像ReLU将ANN的负激活值重置为0一样。但是，由于输入电流的顺序，尽管总电流为负，但在仿真时间内仍会产生脉冲。例如，起初，脉冲神经元继续接收正电流并产生脉冲。然后，它开始接收负电流，直到时间结束。并且总输入电流为负。因此，在这种情况下，发放率是不可预测的，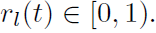
根据上面的讨论，转换过程中的误差是由于在仿真时间结束时缺少剩余的膜电位消息的一部分而引起的。与(Rueckauer et al., 2017)中的结论相反，由于减少了膜电位引起的误差，神经元的发放率略低于相应的激活值，实际上，发放率不存在确定大小与相应激活值的关系。增加仿真时间可以减小误差。并且我们观察到最后一层的发放率通常低于相应的激活值。这可以部分解释为，由于
是最常见的情况，因此发放率的总体趋势正在降低。因此，逐层累积的误差和最终发放率低于激活值。
Methods to Alleviate the Error
在本节中，我们介绍了一组减小转换过程中误差的方法。
Parameter Normalization (Diehl et al., 2015)提出了第一个基于数据的参数归一化，(Rueckauer et al., 2017)对其进行了改进。该操作的目的是将激活值缩放到与发放率相同的范围。然后可以将权重和偏差直接映射到SNN中。它使用训练集来收集每个ReLU层的所有最大激活值。通过除以这些最大值，所有ReLU激活值均缩放为[0, 1]。
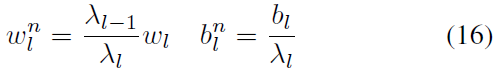
其中
和
是归一化权重和偏差。wl和bl是原始权重和偏差。λl是第 l 层的最大ReLU值。
基于观察到一些激活值明显大于其他激活值，这将使大多数激活值显著小于1(Rueckauer et al., 2017)改进了归一化方法并提出了一种更可靠的方法。他们没有使用该层的最大激活值进行归一化，而是使用该层的第p个百分位激活值。P是一个超参数，通常在[99.0, 99.999]范围内具有良好的性能。该方法旨在提高发放率，从而减少延迟，直到脉冲到达较深的层为止。
在深度RL任务中，我们发现转换后的SNN的性能对超参数p(百分数)非常敏感。它不仅减少了各层之间的延迟，而且还大大提高了从DQN转换的SNN的性能。这是因为通过调整百分数，发放率增加，并且由剩余膜电位引起的误差被部分补偿。因此，减小了原始DQN与转换后的SNN之间的精度差距。在这项工作中，我们假设所有脉冲神经元都具有相同的阈值。尽管有一些工作可以通过分别调整不同层中的阈值来减少误差(Sengupta et al., 2019)。从理论上讲，它实际上与更改参数归一化的百分数具有相同的效果。
Robust Firing Rate 根据公式(7)，误差与仿真时间成反比。我们设置的仿真时间越长，对发放率的影响就越小。但是，更长的仿真意味着更低的功耗效率。因此，这是精度和效率之间的权衡。通常，总仿真时间设置为100-1000个时间步骤。实际上，发放率是离散的，且仿真时间有限。如上所述，不同动作之间的q值非常接近。这使得SNN的最后一层中的脉冲神经元有时会收到相同数量的脉冲，从而导致相同的发放率。当仿真时间不够长时，这种情况尤其常见。为了区分具有相同发放率的脉冲神经元之间的实际最优动作。我们介绍了剩余的膜电压来解决这个问题。这种方法的直觉是具有较高膜电位的神经元更有可能产生下一个脉冲。因此，当多个神经元具有相同的发放率时，我们应该选择膜电位最高的神经元。从理论上讲，增加膜电位也有其自身的好处。根据公式(13)，
是我们可以直接获得的唯一误差部分。Vl(t)恰好是仿真时间结束时的膜电位。结合公式(7)，增加膜电位可以消除最后一层的误差，这使SNN的发放率更接近ANN的激活值。
其中rlast(t)和Vlast(t)是在时间 t 最后一层的脉冲神经元的发放率和膜电位。flast(t)是在时间 t 的最后一层中脉冲神经元发放率更鲁棒的表征。鲁棒的发放率不仅提高了精度，而且减少了时延。这使得SNN花费更少的仿真时间来区分不同动作之间的大小关系。
Results
在本节中，我们使用17个Atari游戏评估我们的方法。
Environment 街机学习环境(ALE) (Bellemare et al., 2013)是一个平台，可为数百个Atari 2600游戏环境提供接口。它旨在评估通用且独立于领域的AI技术的发展。智能体通过游戏的图像帧获得环境状况，该图像帧被修改为84x84像素，最多用18种可能的动作与环境交互，并以游戏得分变化的形式接收反馈。由于(Mnih et al., 2015)在Atari游戏中显示了对智能体的人工控制，因此Atari游戏已成为深度RL的基本基准，而ALE是Atari游戏非常受欢迎的平台。
在没有专用SNN硬件的情况下，模拟基于发放率的SNN是一项计算量很大的任务，特别是对于RL任务。我们选择使用BindsNET (Hazan et al., 2018)模拟SNN。BindsNET是第一个也是唯一的用于在PyTorch平台上仿真SNN的开源库(PS：目前还有SpikingJelly等平台)。它利用GPU的优势，极大地加快了测试SNN的过程。所有结果都在单个NVIDIA Titan-X GPU上运行。
Networks 要获得转换后的SNN，我们需要先训练DQN。我们使用的DQN是(Mnih et al., 2015)提出的朴素DQN，它具有3个卷积层和2个全连接层。第一个卷积层具有32个步幅为4的8x8滤波器。第二个卷积层具有64个步幅为2的4x4滤波器。第三个卷积层具有64个步幅为1的3x3滤波器。全连接层具有512个神经元。最后一层神经元的数量取决于被测试游戏有效动作的数量，我们使用ReLU作为激活函数，该函数应用于除最后一层之外的所有层。所有游戏都使用此架构进行训练。我们使用的超参数也与(Mnih et al., 2015)相同。
Conversion 在获得训练好的DQN之后，我们将其转换为相应的SNN。首先，我们需要使用IF神经元来构建具有与DQN相同架构的SNN。在进行参数归一化之前，我们需要收集游戏帧以计算每一层的第p个最大激活值。对于每个游戏，我们最多收集15000帧以进行参数归一化，然后将这些参数映射到相应的脉冲神经元。最后，我们获得了转换后的SNN。
Metric 对于Atari游戏，在游戏中获得的分数是评估该方法性能的主要指标。但是，有时，如果游戏未运行足够次数，则由于方差，平均得分不能很好地表示性能。为了更有效地测试转换过程的效果并更直接地显示结果，我们引入了一个新指标，即转换率。 它受到图像分类精度的启发，其表示如下：
其中CR是转换率，E是SNN在一场游戏中选择与DQN相同的动作数。NA是智能体在游戏中采取的动作总数。转换率与图像分类任务中的精度非常相似。DQN选择的动作可以视为正确标签的代理。转换率描述了SNN智能体和DQN智能体的行为之间的相似性。可以通过将游戏帧同时输入原始DQN和转换后的SNN来获得转换率，但是智能体仅采取SNN计算的动作。 然后我们可以同时获得SNN的转换率和游戏得分。
Testing 为了测试转换后的SNN的性能，每次运行最多对游戏的每一个epoch进行5分钟(18000帧)的评估。为了测试智能体在不同情况下的鲁棒性，智能体会通过随机次数(最多30次)的无操作动作启动。应用贪婪策略以最小化评估期间过拟合的可能性，其中ε = 0.05。我们使用的发放率是鲁棒的发放率。
The Effect of Simulation Time
图1(a)显示了在四个游戏中具有不同仿真时间的SNN的性能。如果将仿真时间设置为100，则将帧输入到SNN中100次。我们选择的百分位是性能最优的百分位。从图中可以得出结论，随着仿真时间的增加，所有四个游戏的转换率也都得以增加，这与"方法"部分中的结论是一致的，即更长的仿真时间可以减少由剩余膜电位引起的误差，但效果逐渐减弱。这是低误差和低功耗之间的折衷方案。
对于对仿真时间不太敏感的游戏(例如Breakout和James Bond)，即使仿真时间非常短(例如100个时间步骤)，SNN智能体仍然可以在低转换率的情况下保持良好的性能。这些SNN模型更鲁棒，误差始终会影响q值接近的动作之间的大小关系。因此，SNN智能体选择的错误操作仍然可能是次优操作。智能体仍然可以在低转换率下具有良好的性能。对于诸如Star Gunner和Video Pinball之类的游戏，这些游戏对仿真时间更加敏感，较长的仿真时间会导致更大的转换率，从而带来更好的性能。
The Effect of Percentile
图1(b)显示了在四个游戏中具有不同百分数的SNN进行参数归一化的性能。百分位是一个非常敏感的超参数。数值研究表明，当百分数小于99时，我们不太可能获得良好的性能。因此，我们从99开始测试了百分数的效果。对于所有四个游戏，百分数都会极大地影响转化率，而转化率会影响最终分数。对于Breakout和James Bond等游戏，转换率会随着百分数的增加而不断提高。将百分比设置为接近100可以具有良好的性能。对于其他游戏，例如Star Gunner和Video Pinball，随着百分数的增加，性能达到了最高点。在这两个游戏中，百分数99.9给出最大值。一旦超过这一点，这些游戏的性能将急剧下降。该结果表明，调整百分比值可以大大提高智能体在这些游戏上的性能。
The Performance of Converted SNNs on Different Games
表1显示了我们的方法在多种Atari游戏上的性能。由于资源的限制，我们选择17种游戏进行测试。这些是DQN具有很高性能的游戏。仿真总时间为500个时间步骤。我们在[99.9，99.99]中选择最优百分位。每个游戏进行50次。表中显示了DQN和转换后的SNN的平均分数。我们还显示了通过T-Test获得的DQN和SNN的P-Value。我们得出结论，所有SNN的分数都接近DQN的分数。而且，除了Kull和Star Gunner之外，几乎所有游戏在DQN和SNN之间没有显著差异。这表明通过我们的方法转换后的SNN具有与原始DQN相当的性能。
Conclusions and Future work
这项工作通过将DQN参数转换为SNN解决了使用SNN解决深度RL问题的问题。
- 我们提出了一种鲁棒的转换方法，该方法可以减少转换过程中引起的误差。我们在17种Atari游戏上测试了该方法，结果表明SNN可以达到与原始DQN相当的性能。
- 重要的是要指出，与(Rueckauer et al., 2017)提出的等效模拟激活值相比，我们的方法提供了脉冲神经元发放率的更准确近似值。我们的工作纠正了以前转换方法的一些不正确之处，并进一步发展了该理论。
- 据我们所知，我们的工作是第一个在具有SNN的多种Atari游戏上实现高性能的工作。它为在具有专用硬件的实时系统上高效运行RL算法铺平了道路。
- 我们对一些游戏的转换率不是很高。SNN智能体采取了一些动作，而不是最优动作，这会降低这些游戏中SNN的鲁棒性。这些问题的原因是正在进行和将来研究的目的。
Supplymentary Material
表2显示了我们的方法在17种Atari游戏上的详细性能。仿真总时间为500个时间步骤。每个游戏进行50次。我们显示了两个不同的百分数99.9和99.99的SNN得分和转换率，它们更有可能具有良好的性能。SNN分数是通过鲁棒的发放率获得的。同时，我们还显示了使用正常发放率的SNN转换率。从表中可以得出结论，与正常发放率相比，鲁棒的发放率可以显著提高转化率。通过调整百分比，与DQN相比，SNN可以具有可比的性能。