emm, 这应该不能算作学习笔记, 只是简单的记录。
笔记应当等到学习完的很长一段时间后再写, 加深理解,以免误导。
例题
这两道题我是当做板子来学习扫描线的, 比较有启发性
板子
给出若干个矩形, 求面积并
(这题我曾经瞎搞写出来过, 具体做法是切割矩形, 把相交的矩形切成最多4个, 当时的写法很妙
果树
给定一棵树, 每个点有颜色, 每种颜色的点不超过20, 求不经过同颜色的点的路径数量
(没写出来, 当板子的
扫描线
他可以用来求矩形的面积并
思想很容易理解: 把矩形离散化后,用一条线扫过去,其实就是吧原图分成很多段, 把每一段的覆盖面积之和求出来,
容易发现, 这样分成的很多段, 面积都等于覆盖长度乘上高度, 问题就变成了维护覆盖长度
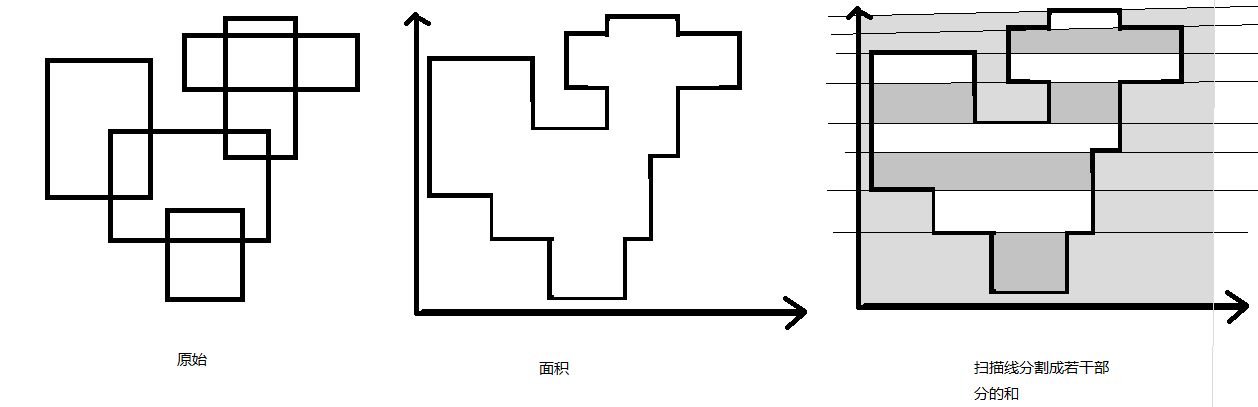
很多博客十分详细的在讲上面的过程, 但这其实是很好理解的:面在某种意义上是由线组成的(如果你刚学,可以先看看去他博客 )
线段树维护覆盖长度
大多博客讲完算法的思想之后就直接上代码,这让我难以理解, 我通常喜欢学习完做法之后自己实现,不看题解代码
然后我发现我更本不知道怎么实现
线段树维护区间长度?实际上是:实现一颗支持区间修改, 区间查询大于0的数的个数的线段树?
不对啊,我想过好几次类似的东西, 应该不可能实现吧
特殊性质, 题解里说线段树中的值不会小于0? 有什么用吗???? 万一我对某一区间减一, 导致他的一个子区间变成了0,而其他没有呢????
长时间研究后,我终于弄懂了:
我们之所以可以维护这么一个东西,是因为一条性质:
当我们把一个区间整体减一时, 同一个区间一定在之前的某一时刻被整体加一
也就是说: 修改的区间一一对应
然后, 我们对于线段树上面的每一个节点, 维护一个lazy和val
val好理解,他表示这颗子树代表的区间中有多少大于0的点
关键是lazy,很容易让人理解为懒标!不,扫描线的线段树是没有懒标的!
所谓懒标, 是当我们对某一区间修改的时候, 为了降低复杂度, 只修改这一个节点, 把标记延迟到需要用到子节点的时候才下传
关键是: 懒标是延迟下传, 而由于扫描线的特殊性质, lazy这个东西压根就不用下传, 所以不用懒标复杂度就是对的。
我们得以重新审视:
这个lazy实际上表示, 这个区间被整体加了几次, 当我们进行修改操作时, 如果当前区间整个都会被修改, 我直接吧lazy加一
否则的话我去修改他的子区间,
还有一个特殊的操作是push_up, 如果当前区间的lazy不为0, 则让val等于区间长度
否则等于他两个子树的val和
仔细思考一下, 你会发现,由于特殊性质的存在, 这样做一定是对的。
先写到这吧 , 有点累
再深入点就等下次写学习笔记吧......