P1110 [ZJOI2007]报表统计

传送门

---

emm， 也不用什么权值线段树平衡树啊， set+单点修改不查询的线段树都接近最优解了......

好想而且很好写， 常数也不大。

---

题意

有n堆数，初始每堆只有一个数， 从左往右排成一列。
三种操作：

1.往某一堆的末尾插入一个数
2.查询相邻两个数的差值(绝对值)的最小值
3.查询任意两个数的最小差值(绝对值).

题解

emm, 由于根本没有删除操作， 那不是好像很好做的样子！
第三种操作， 每次插入数字的时候， 用set维护一下前驱后继即可。

考虑第二种操作， 大概是这么一个东西

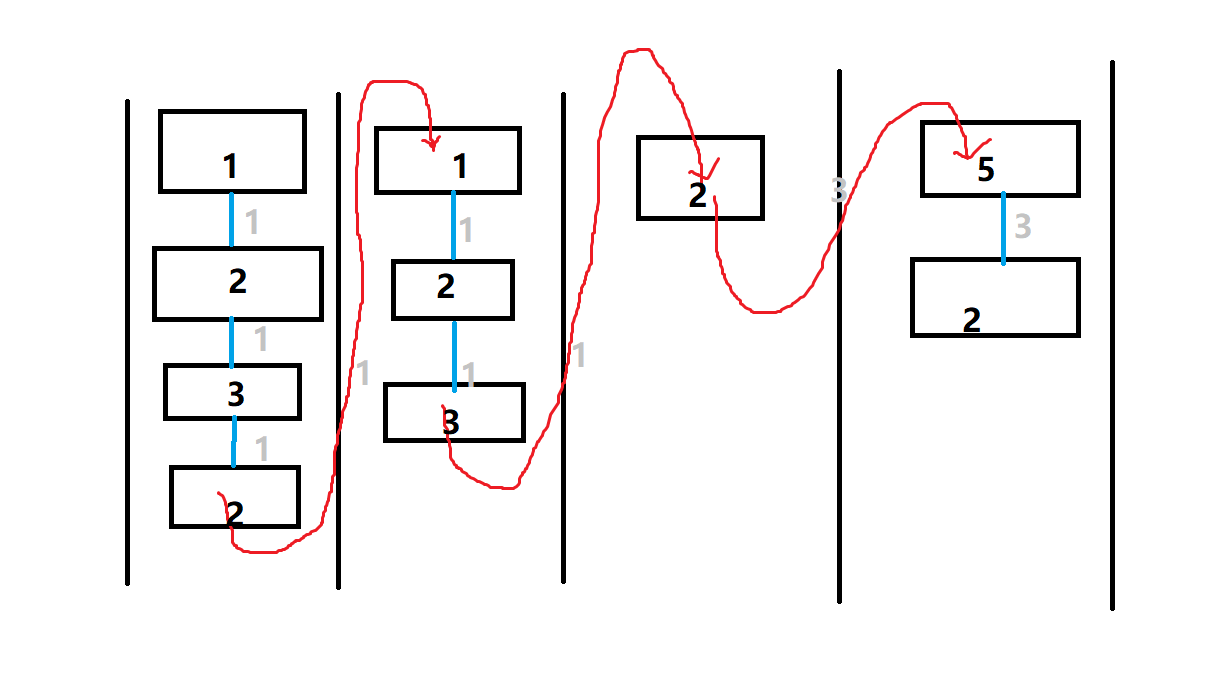
每一列表示一堆， 蓝色和红色的边表示相邻的元素， 以及他们的差值
我们只需要维护它的最小值就行了，

可以发现蓝色的边是稳定的, 不会消失。 每次插入一个数的时候会和它上面的的那个数产生一条蓝边， 用一个变量维护最小值即可。

然后红边就不一样了， 它是会消失的。 我插入一个数的时候， 这一堆数原来的红边就消失， 新的红边出现。

但事实上，每一堆至多有一个红边， 用一个线段树维护它的最小值即可，
每次插入是时修改一个当前红边的值， 即可
线段树只需单点修改， 甚至不需要查询（直接用tree[1]即可， 即根节点的权值

实现

#include <iostream>
#include <cstdio>
#include <set>
#include <vector> 
#define l(x) (x*2)
#define r(x) (x*2+1) 
using  namespace std;

inline int read(){
	int num=0, flag=1; char c=getchar();
	while(!isdigit(c) && c!='-') c=getchar();
	if(c=='-') flag=-1;
	while(isdigit(c)) num=num*10+c-'0', c=getchar();
	return num*flag; 
}

inline int reads(){
	int num=0; char c=getchar();
	while((c<'A' || c>'Z') && c!='_') c=getchar();
	while((c>='A' && c<='Z') || c=='_') num++, c=getchar();
	return num;
}

inline int abs(int x){
	return x<0?-x:x;
}

const int N = 600600;
const int inf = 0x3f3f3f3f;
int n, m, minv=inf, ming=inf;
int a[N], las[N];
set<int> s;

struct segTree{
	int tree[N<<2];
	void push_up(int o){
		tree[o] = min(tree[l(o)], tree[r(o)]);
	}
	
	void build(int o, int l, int r){
		tree[o] = inf;
		if(l == r) return ;
		
		int mid = (l+r)/2;
		build(l(o), l, mid);
		build(r(o), mid+1, r);
	}
	
	void update(int x, int v, int o=1, int l=1, int r=n){
		if(l==r) {
			tree[o] = v;
			return ;
		}
		int mid = (l+r)/2;
		if(x <= mid) update(x, v, l(o), l, mid);
		else update(x, v, r(o), mid+1, r);
		push_up(o);
	} 	
}t; 

inline void insert(int v){
	if(minv) {
		if(s.count(v)) {
			minv = 0;
		}else{
			int res = inf;
			
			auto x = s.lower_bound(v);
			if(x!=s.begin()) x--, res = min(res, abs(*x-v));
			x = s.upper_bound(v);
			if(x!=s.end()) res = min(res, abs(*x-v));
			
			minv = min(minv, res);
			
			s.insert(v);
		}
	}
}

int main(){
	n=read(), m=read();
	t.build(1, 1, n);
	
	for(int i=1; i<=n; i++){
		a[i] = las[i] = read(); 
		insert(a[i]); 
	}
	for(int i=1; i<n; i++) t.update(i, abs(las[i] - a[i+1]));
	
	while(m--){
		int type = reads();
		if(type == 6){
			int x=read(), v=read();
			insert(v);
			
			ming = min(abs(las[x] - v), ming); 
			las[x] = v;
			
			if(x != n) t.update(x, abs(las[x] - a[x+1]));
		}else if(type == 7){
			printf("%d
", min(ming, t.tree[1]));
		}else{
			printf("%d
", minv);
		}
	}
	 
	return 0;
}