支持向量机

支持向量机

• 优化目标
• 支持向量机背后的数学原理
• • 问题转换
  • 正式推导
• 核函数
• • 选择landmarks
  • 支持向量机的参数

 支持向量机作为一个分类器在分类问题之中有着广泛的应用，其思想和逻辑回归相似，但是其作为大间距分类器做出的分类效果比不同的逻辑回归要好一些。让我们来看看，到底什么是支持向量机，其内部的数学原理是什么。

优化目标

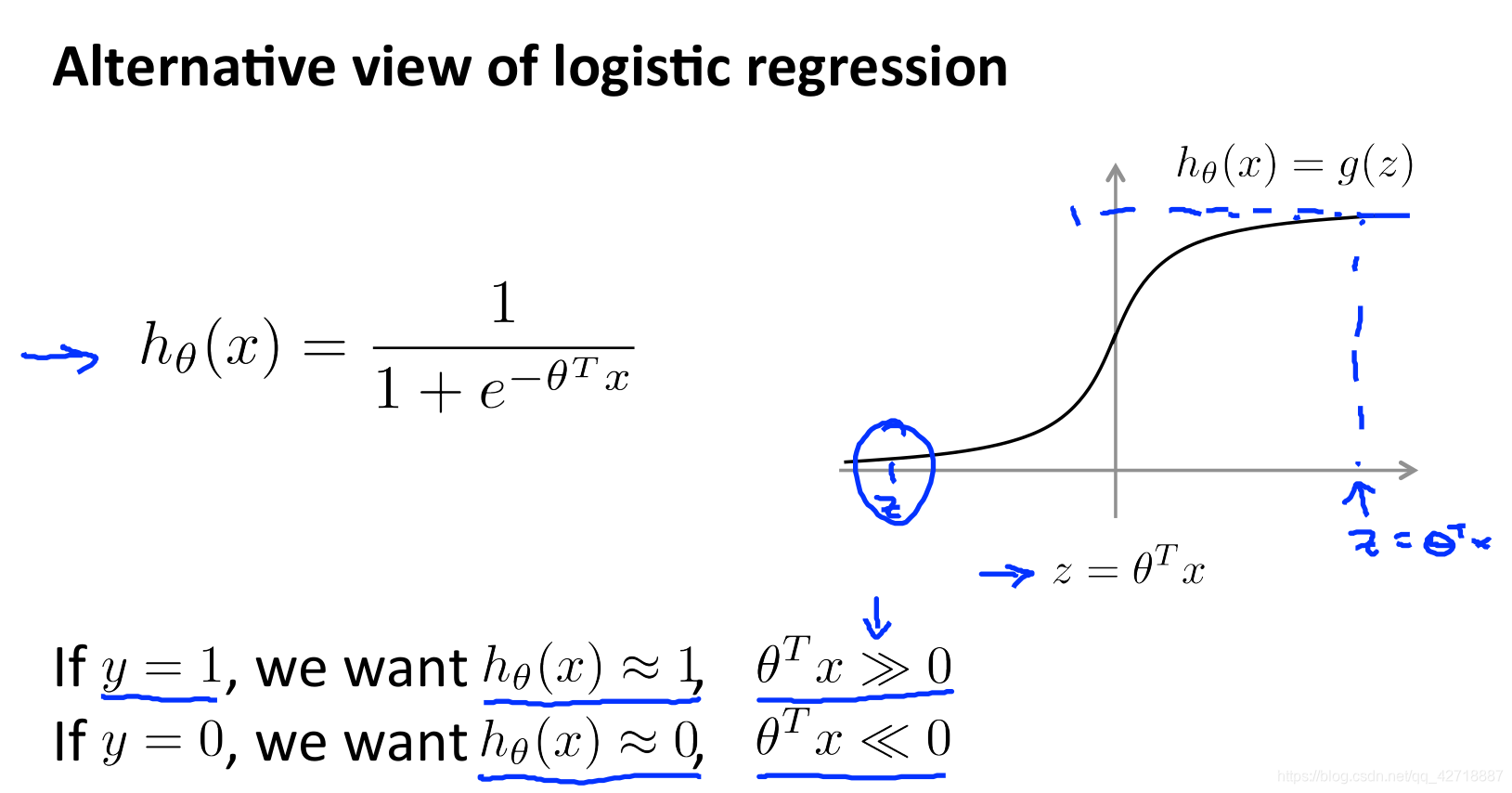 首先让我们来回顾一下逻辑回归的假设函数，在这里我们要想输出h(x)≈1的话就需要theta.T * x远大于0。
 然后我们又来看一看逻辑回归的损失函数，画出来如图的两个函数图像。如果我们把函数改为蓝色的折线形式的话，就成为支持向量机的损失函数（至于为什么需要这样进行设定，后面的数学原理会介绍的）。
 这个就是支持向量机的损失函数，和逻辑回归稍微有点不同，其实这里C和lamba都是起到了惩罚的作用。
 我们把cost函数修改之后，如果y=1的话，就需要在优化的时候theta.T * x ≥ 1（就不仅仅是大于0就行了，假设函数还是theta.T * x≥0不变） 。
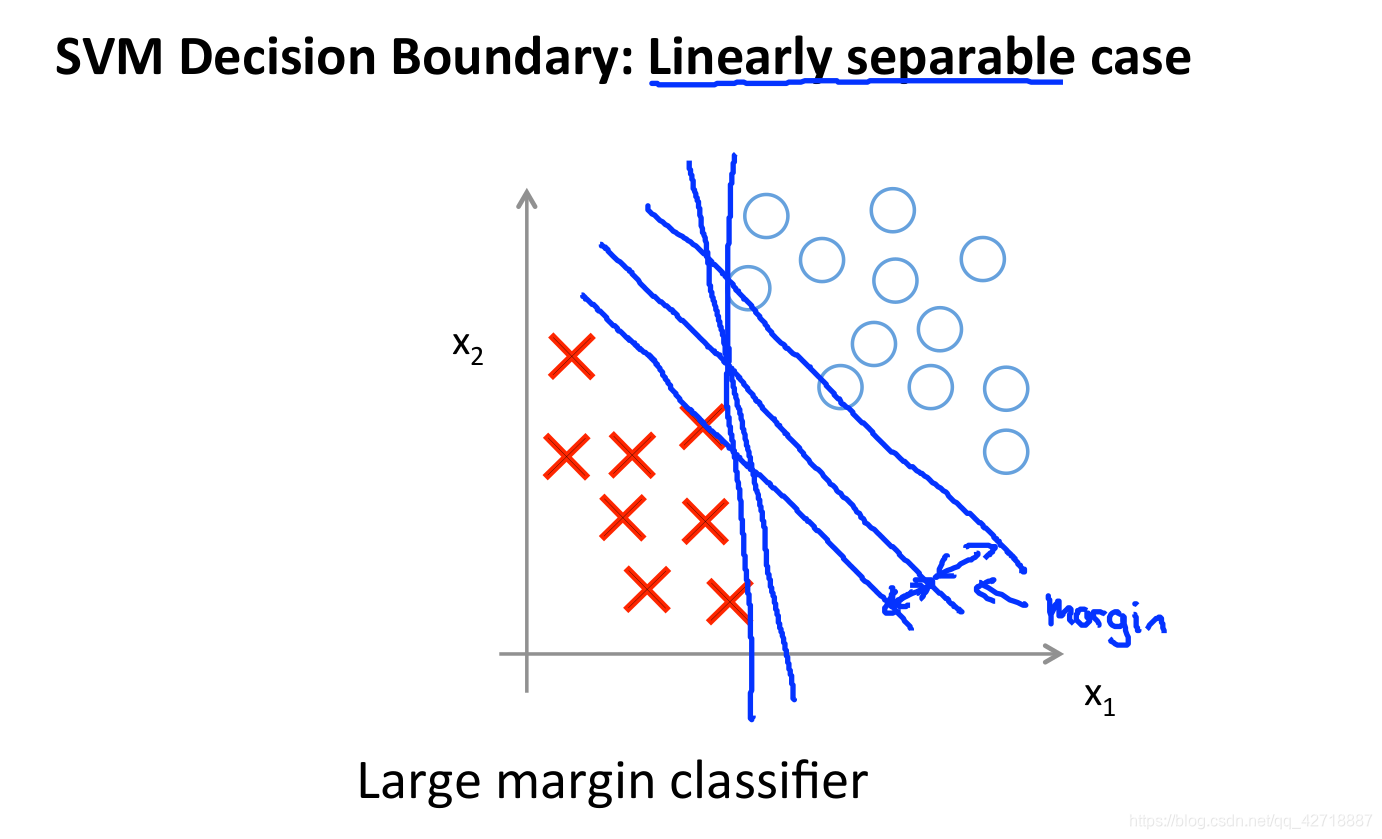
 从上面的推导就可以得到支持向量机的决策边界，而且这个边界是一个大
间距的边界，如下图所示。

支持向量机背后的数学原理

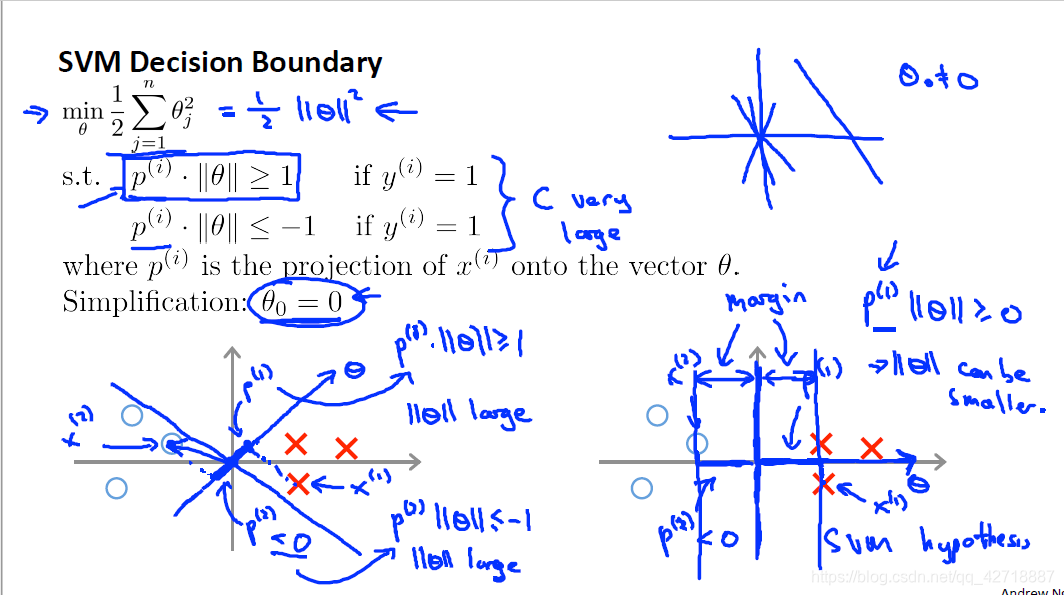
 让我们来看一看支持向量机的优化目标，其目的就是优化θ的平方和最小（注意这里就不在是正则化惩罚项了）。我们将，数据在二维平面中展示出来，所以现在支持向量机所要做的就是寻找到一条直线将两种数据分开。

问题转换

 但是，为什么支持向量机寻找到的直线与两种数据间的间距会比其他的方法大一些。首先，θ的平方和就是θ向量的内积由高中所学的知识就能知道，θ向量与自己的内积就相当于模长的平方。所以最后的问题转换为将θ的模长优化到最小。

正式推导

 然后我们再来看看我们的预测函数$\theta .T\ast x$≥0(if y = 1),这个式子也就是θ与x的内积，也就相当于x在θ的投影与θ模长的乘积，所以需要将x在θ的投影变大，由预测边界直线与θ正交（高中学的）可知，x在θ的投影变大的话，x到决策边界直线的距离也就会变大，所以就形成了大间距的分类边界。

核函数

 前面我们讲了支持向量机的线性分类，但是现实中的分类一般都不会是线性的。所以通过怎样的变化能够让支持向量机完成非线性分类呢？联系到以前所学的线性回归变成多项式回归就是从线性变到非线性去，所以我们要想实现支持向量机的非线性分类就需要完成原始特征到新特征的映射。那怎样完成这样的映射呢？这里就需要我们使用一个叫核函数的东西。

 上图就是高斯核函数，我们先在平面上选择三个landmark，然后利用高斯核函数计算与$x^{(i)}$与每一个landmark的值（也就是与landmark的相似的值，这里学过正态分布的话很容易理解），有三个landmark就会提取出三个feature，所以我们不在用$x_1$，$x_2$来表示$x^{(i)}$的特征，而是使用$f_1$,$f_2$,$f_3$来表示特征，这样就完成了线性到非线性的映射。

选择landmarks

 从上面的推导也可以看出来，选择landmarks是非常重要的一件事情。这里一般的做法就是把所有的$x^i$作为landmarks吗，所以每一个$x^i$所提取出来的特征就是m个（这里是没有加$f_0$）。

支持向量机的参数

 这里c参数就没什么好说的作用和$1/\lambda$差不多。而$\sigma$越大，核函数越不平滑也就是越不敏感，就会导致高偏差，而越小的话核函数就越敏感也就会导致高方差。
 这里再附上一张逻辑回归和支持向量的选择比较，供大家参考一下。