「学习笔记」动态规划 I『初识DP』

写在前面

注意：此文章仅供参考，如发现有误请及时告知。

更新日期：2018/3/16，2018/12/03

---

动态规划介绍

动态规划，简称DP(Dynamic Programming)
简介1 简介2

动态规划十分奇妙，它可以变身为记忆化搜索，变身为递推，甚至有时可以简化成一个小小的算式。

动态规划十分灵活，例如 NOIP2018 PJ T3 摆渡车 ，写法有很多很多，但时间、内存却各有差异。

动态规划十分简单，有时候一个小小的转移方程就能解决问题。

动态规划十分深奥，有时你会死也想不出合适的转移方程，有时你会被后效性困扰，有时动态规划的同时还有许多蜜汁优化。

动态规划在NOIP中十分重要，我目前为止参加的(NOIP_{2017 PJ} & NOIP_{2018PJ})都有一道动态规划，而且都是(T3)。(估计普及考纲比较窄，要出难题只有DP了)

---

问题引入

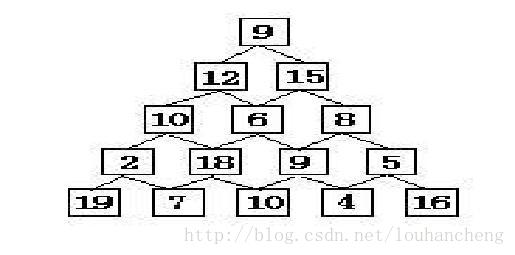
还是这道题...... 数塔问题！！！

这里我们选择动态规划来解决.
我们不难理解，对于每一个元素，它到顶层的最大值是确定的，也就是说，从顶层到任何一个元素的最大值都是确定的.比如，对于第3层的第2个元素6，顶层到它的最大值只有一个（9 + 15 + 6 = 30）（但不代表路径只有一条），不会改变.

所以，我们用一个数组dp来存储从元素(i, j)到底层的最大值.

#define MAXN 100
int dp[MAXN + 5][MAXN + 5];

仔细观察分析，不难发现，对于每一个元素dp[i][j],都存在

dp[i][j] = max( dp[i + 1][j], dp[i + 1][j + 1] ) + a[i][j];

即每一个元素到(1, 1)的最大值都是上一层与它相连的两个元素中较大的一个，再加上这个元素本身的值. 最后的答案即为dp[1][1].

不过，我们自顶向下分析，但是却要自底向上实现，即从最顶层开始分析，写代码时却要注意for语句要倒过来写：

for ( int i = N; i >= 1; --i )
	for ( int j = 1; j <= i; ++j )
		dp[i][j] = max( dp[i + 1][j], dp[i + 1][j + 1] ) + a[i][j];

为什么会这样呢？其实不难分析，在算dp[i][j]时，你必须确保dp[i + 1][j] 和 dp[i + 1][j + 1]已经完成，如果没有完成，dp[i + 1][j] 和 dp[i + 1][j + 1]的值就是错误的，算出的dp[i][j]也是错误的，这样结果就不对了。而反过来做，你就会发现i从大的开始，在做dp[i][j]的时候dp[i + 1][1 ~ N]都已经做过了。还有，要注意，动态规划的初始化很重要，有时初始化就会决定你结果对不对。这里的初始化很简单，现在给出两种方法：

memset( dp[N + 1], 0, sizeof( dp[N + 1] ) );//即把dp[N + 1][0...]全部初始化为0.
for ( int i = 1; i <= N; ++i )
	dp[i] = a[i];
//下面这个与上面等价：
copy( a[N] + 1, a[N] + N + 1, dp[N] );// copy( 开始地址, 结束地址, 放到的数组 ); copy( a, a + n, b );即为把a数组下标为0~n按次序复制到b数组.
//当然，这样写，实现时要注意少一层循环：(下面这个是修改后的)
for ( int i = N - 1; i >= 1; --i )
	for ( int j = 1; j <= i; ++j )
		dp[i][j] = max( dp[i + 1][j], dp[i + 1][j + 1] ) + a[i][j];
//至于为什么这样，这里不再赘述，请自己思考. 

这里再完整地放一放代码，实在不会写的可以参考.

#include<bits/stdc++.h>
using namespace std;
#define MAXN 100

int C, N;
int a[MAXN + 5][MAXN + 5];
int dp[MAXN + 5][MAXN + 5];

void solve(){
	scanf( "%d", &N );
	memset( dp, 0, sizeof dp ); 
	for ( int i  = 1; i <= N; ++i )
		for ( int j = 1; j <= i; ++j )
			scanf( "%d", &a[i][j] );
	for ( int i = N; i >= 1; --i )
		for ( int j = 1; j <= i; ++j )
			dp[i][j] = max( dp[i + 1][j], dp[i + 1][j + 1] ) + a[i][j];
	printf( "%d
", dp[1][1] );
}

int main(){
	scanf( "%d", &C );
	while( C-- ) solve();
	return 0;
}

事实上，可以做一个优化：去掉dp数组，直接用a数组来做：(节约空间，人人有责)

#include<bits/stdc++.h>
using namespace std;
#define MAXN 100

int C, N;
int a[MAXN + 5][MAXN + 5];

void solve(){
	scanf( "%d", &N ); 
	for ( int i  = 1; i <= N; ++i )
		for ( int j = 1; j <= i; ++j )
			scanf( "%d", &a[i][j] );
	for ( int i = N - 1; i >= 1; --i )
		for ( int j = 1; j <= i; ++j )
			a[i][j] += max( a[i + 1][j], a[i + 1][j + 1] );
	printf( "%d
", a[1][1] );
}

int main(){
	scanf( "%d", &C );
	while( C-- ) solve();
	return 0;
}

至于为什么，请诸位自己理解（很好理解的，选个小一点的数据自己算一算就知道了）。

---

总结

怎么样，找到些感觉了吧？现在我们来学习怎么写动态规划的程序.

第一步，我们要观察题目是否可以用动态规划实现。怎么判断呢？我们要看它是否可以分成几个阶段，如上题，可以分成1~N层共N个阶段，每个阶段还可以分成1~i个元素共i个小阶段。然后，我们要看看每个阶段的答案是不是确定的，上题中，每一个元素到底层的最大值就是确定的。再看看每个阶段是不是有关联，如果有，还要确定有什么关联，是否对于每一个阶段都满足。

第二步，就是确定关联啦。怎么确定呢？我们要仔细分析题目，观察每两个阶段之间的关系。动态规划的重点也就在这里，关联确定了，动态规划基本上就可以写下来了。

第三步，确定边界条件，比如，上题就要把dp[N+1][...]全部赋值为0，否则就会出错。

除此之外，还要确定完成的顺序，要做某个阶段，它需要用到的阶段必须先做完。

当然，有时还要添加滚动数组、优化等。

这样，一个动态规划程序就完成啦。

---

尾声

当然，动态规划还有许多分支（背包DP、区间DP等），以上讲的都是最表皮的。那些难一点的，都只好下次再讲吧。

最好拿点题目来练一下：洛谷的DP