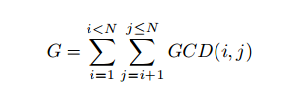UVA 11426 GCD

题目是给出N，求G的值。

可以转化为S(n) = f(1) + f(2) + f(3) + ... + f(n)。其中f(n) = gcd(1, n) + gcd(2, n) + ... + gcd(n, n)。

随便写一个n = 5 的情况。得到gcd(1, 5) = 1, gcd(2, 5) = 1, gcd(3, 5) = 1, gcd(4, 5) = 1, gcd(5, 5) = 5。

所以当f(5) = 1 * 4 + 5 * 1 = 9。显然我们可以根据公约数的值来计算f(n)的值。设gcd(x, n) = i, 可以得到gcd(x / i, n / i) = 1。也就是(x / i)与(n / i)互质，可以通过欧拉函数来计算（x / i）的数量。为了提高效率，可以枚举约束i，再枚举i的倍数n在线性时间内进行预处理

#include<bits/stdc++.h>
using namespace std;
const int maxn = 4000010;
#define ll long long
int phi[maxn];
ll s[maxn], f[maxn];
void phi_table(int n) {
    memset(phi, 0, sizeof(phi));
    phi[1] = 1;
    for(int i = 2; i <= n; i++) if(!phi[i])
        for(int j = i; j <= n; j += i) {
            if(!phi[j]) phi[j] = j;
            phi[j] = phi[j] / i * (i - 1);
        }
}
int main() {
    phi_table(maxn);
    memset(f, 0, sizeof(f));
    for(int i = 1; i <= maxn; i++)
        for(int n = i * 2; n <= maxn; n += i) f[n] += i * phi[n/i];

    s[2] = f[2];
    for(int n = 3; n <= maxn; n++) s[n] = s[n-1] + f[n];

    int n;
    while(~scanf("%d", &n)) {
        if(n == 0) break;
        cout << s[n] << endl;
    }
}