JZ8 跳台阶
题目描述
一只青蛙一次可以跳上1级台阶,也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法(先后次序不同算不同的结果)。
示例1
输入
1
返回值
1
示例2
输入
4
返回值
5
思路1:直接递归
本质还是fibonacci,不过第一位和第二位变成1了
public class Solution {
//本质还是fibonacci
public int JumpFloor(int target) {
if(target <= 1) return 1;
return JumpFloor(target-1) + JumpFloor(target-2);
}
}
思路2:用数组记忆计算过的
通过数组存放计算后的结果,防止二次计算,减小时间复杂度
public class Solution {
//本质还是fibonacci,不过前两位改为了1 1
public int JumpFloor(int target) {
int [] result = new int [target + 1];
result[0] = result[1] = 1;
if(target <= 1) return 1;
for(int i = 2; i <= target; i++){
result[i] = result[i-1] + result[i-2];
}
return result[target];
}
}
思路3: 只存储两位的动态规划
public class Solution {
//本质还是fibonacci,不过前两位改为了1 1
public int JumpFloor(int target) {
int a = 1;
int b = 1;
int c = 0;
if(target <= 1) return 1;
for(int i = 2; i <= target; i++){
c = a + b;
a = b;
b = c;
}
return c;
}
}
JZ9 变态跳台阶
题目描述
一只青蛙一次可以跳上1级台阶,也可以跳上2级……它也可以跳上n级。求该青蛙跳上一个n级的台阶总共有多少种跳法。
示例1
输入
3
返回值
4
思路1:暴力
称跳到第i级台阶为f[i],跳上第n级为f[n]
在跳上第n级台阶的前一步:
- 一步上去,可能的方案有f[n-1]种
- 两步上去,可能的方案有f[n-2]种
以此类推,f[n] = f[n-1] + f[n-2] + ...+ f[0]
public class Solution {
public int JumpFloorII(int target) {
if(target == 0 || target == 1) return 1;
int []f = new int [target+1];
f[0] = f[1] = 1;
for(int i = 2; i <= target; i++){
for(int j = 0; j < i; j++)
f[i] += f[j];
}
return f[target];
}
}
思路2 进一步优化
因为f[n-1] = f[n-2] + ... + f[0],所以f[n] = f[n-1] * 2;
所以类似前面青蛙跳台阶的解法,可以只存储前一个台阶的方法数即可。
public class Solution {
public int JumpFloorII(int target) {
if(target == 0 || target == 1) return 1;
int a = 1, b = 1;
for(int i = 2; i <= target; i++){
b = a << 1;//left x 2 , right /2
a = b;
}
return b;
}
}
另外,f[0] = f[1] = 1 = 20
f[2] = 2 = 21
f[3] = 4 = 22
所以针对n>=2,f[n] = 2n-1,所以针对这道题的一个更加简便的解法
public class Solution {
public int JumpFloorII(int target) {
if(target == 0 || target == 1) return 1;
return (int)Math.pow(2, target - 1);
}
}
JZ10 矩形覆盖
题目描述
我们可以用21的小矩形横着或者竖着去覆盖更大的矩形。请问用n个21的小矩形无重叠地覆盖一个2*n的大矩形,总共有多少种方法?
比如n=3时,2*3的矩形块有3种覆盖方法:
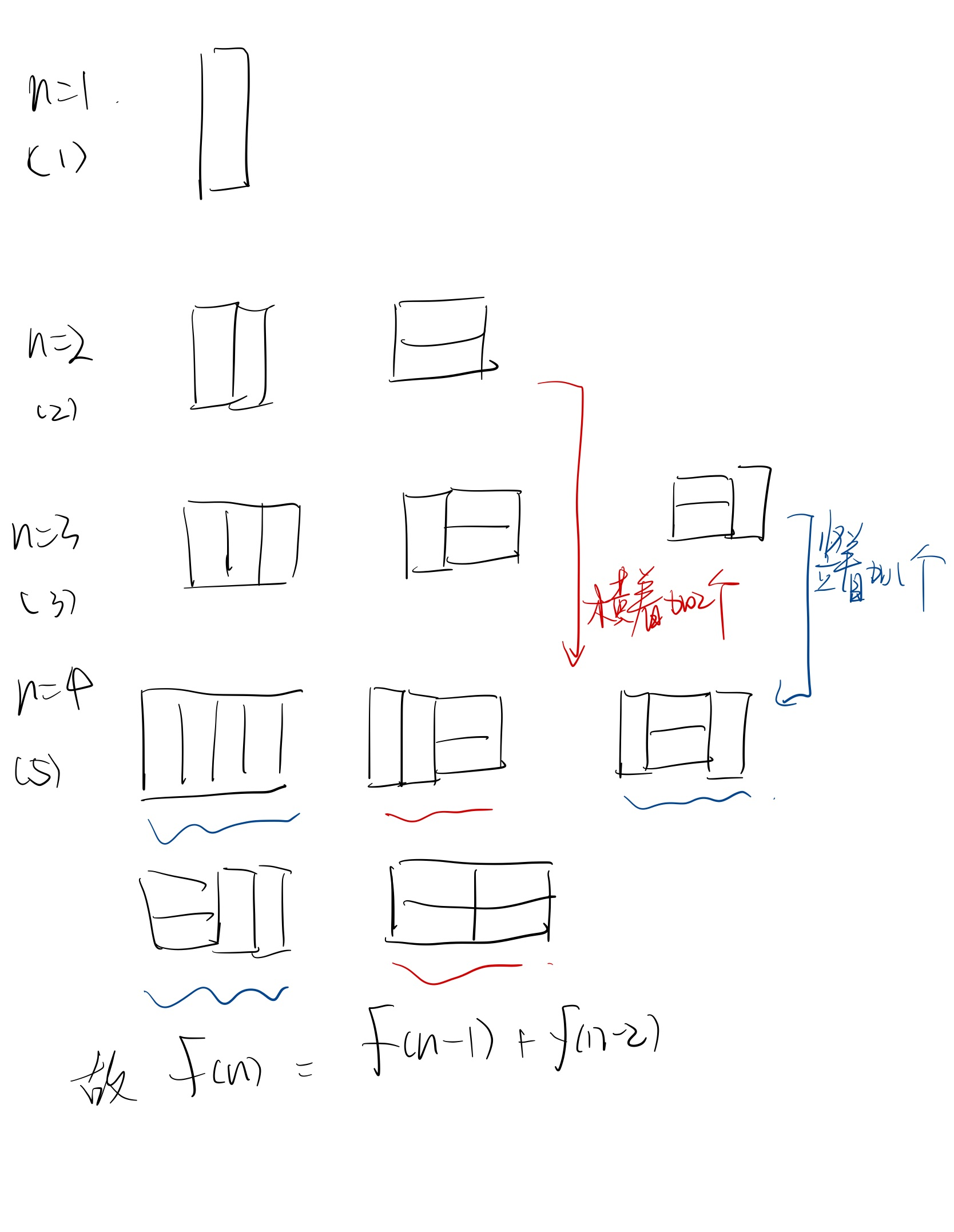
示例1
输入
4
返回值
5
思路 找规律后用递归解决

问题转换为求斐波那契,用数组解决
public class Solution {
public int rectCover(int target) {
int []f = new int[45];
f[1] = 1;
f[2] = 2;
for(int i = 3; i <= target; i++){
f[i] = f[i-1] + f[i-2];
}
return f[target];
}
}
或者存储前两位信息即可
public class Solution {
public int rectCover(int target) {
int a = 1, b = 2, c = 0;
if( target == 1) return a;
if( target == 2) return b;
for(int i = 3; i <= target; i++){
c = a + b;
a = b;
b = c;
}
return c;
}
}