agc046_f Forbidden Tournament
https://atcoder.jp/contests/agc046/tasks/agc046_f

Tutorial
称条件中禁止出现的子图为(H).
首先,考虑若(G)中存在一个入度为(0)的点(v),那么可以将(v)删去,剩下一个(K-1)的子问题.所以接下来只讨论(G)中所有点都有至少一条入边的情况.
随意选择(G)中的某个点(v),设所有存在(v o w)的(w)的集合为(Y),令(X=V(G) setminus Y)(注意(v)在(X)之中).假如(X)中存在一个环,那么一定存在一个三元环(竞赛图性质).而且由于(X)中其他点都是指向(v)的,所以(v)一定不在这个三元环内,那么这个三元环和(v)就组成了(H).所以(X)中一定存在拓扑序(x_1,x_2,cdots,x_k),且(u=x_k),满足对于(i<j),(x_i o x_j)存在.
由于所有点入度不为(0),所以一定存在某条边(w o u),其中(w in Y,v in X),再考虑某个存在(w o w')的(w'),此时的情况如[图1].那么为了不出现(H),边(w' o u)一定存在.那么如果(w)可以到达的点的集合中存在环,那么某个三元环一定和(u)组成了(H)[图2].而且如果(w)不能到达的集合中存在环,那么某个三元环一定和(w)组成了(H)[图3].所以(Y)中也不存在环,所有有拓扑序(y_1,cdots,y_l)满足对于(i<j),(y_i o y_j)存在.
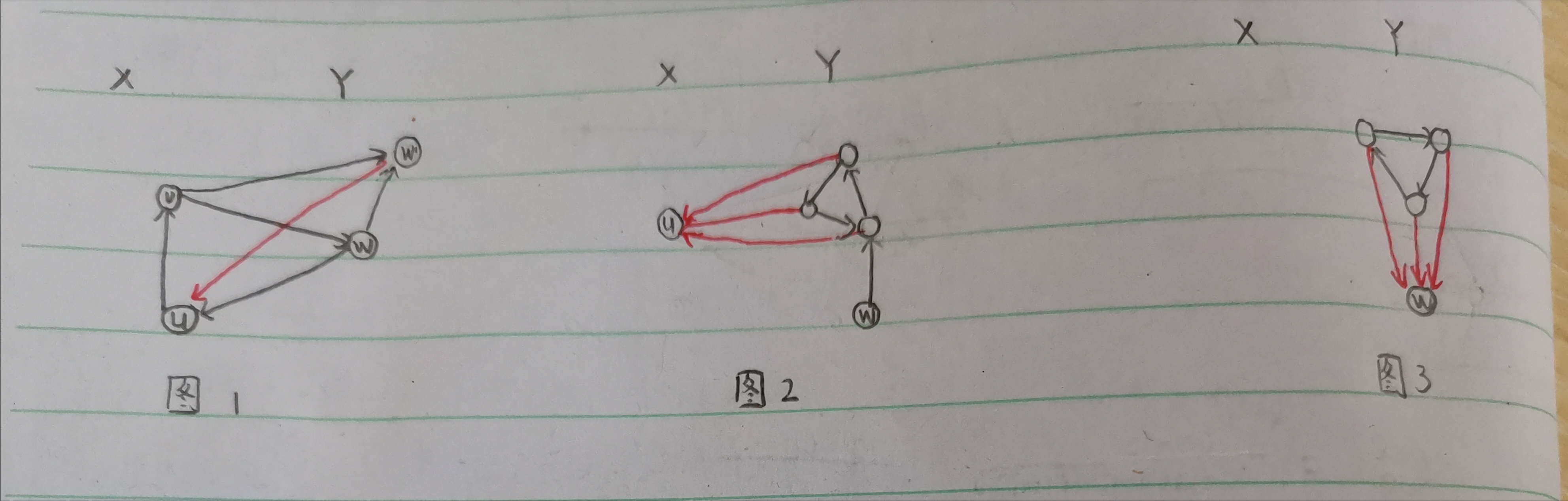
(X,Y)中边的方向确定了,现在考虑(X,Y)之间的边的情况.根据之前的结论,若(y_j o x_i)存在,那么对于(j' in [j,l]),(y_{j'} o x_i)也一定存在.所以如果(x_1 o y_l)存在,那么对于所有(jin[1,l]),(x_1 o y_j)存在,那么(x_1)的入度就是(0),矛盾.所以(y_l o x_1)一定存在.
对于(2 le i le k),假设(x_i o y_l)存在.如果对于某个(i'>i),存在(y_l o x_i'),那么(x_i,x_i',y_l,x_1)就构成了(H)[图4].所以,若(x_i o y_l)存在,那么(x_{i'} o y_l)也存在.设(t)为最大的数使得(y_l o x_t)存在,设(i in [1,t],j in [1,l-1]),且(x_i o y_j)存在.那么(x_i,y_j,y_l)构成了三元环,且对于(i<i' le k),要么(x_{i'} o y_j)存在,要么(x_{i'} o y_l)存在,否则图中将包含(H)[图5].而且根据上一段的结论,若存在(y_j o x_{i'}),那么(y_l o x_{i'})也会存在,所以一定存在(x_{i'} o y_j).所以若存在(y_j o x_i),那么对于所有(i'<i),(y_j o x_{i'})存在.
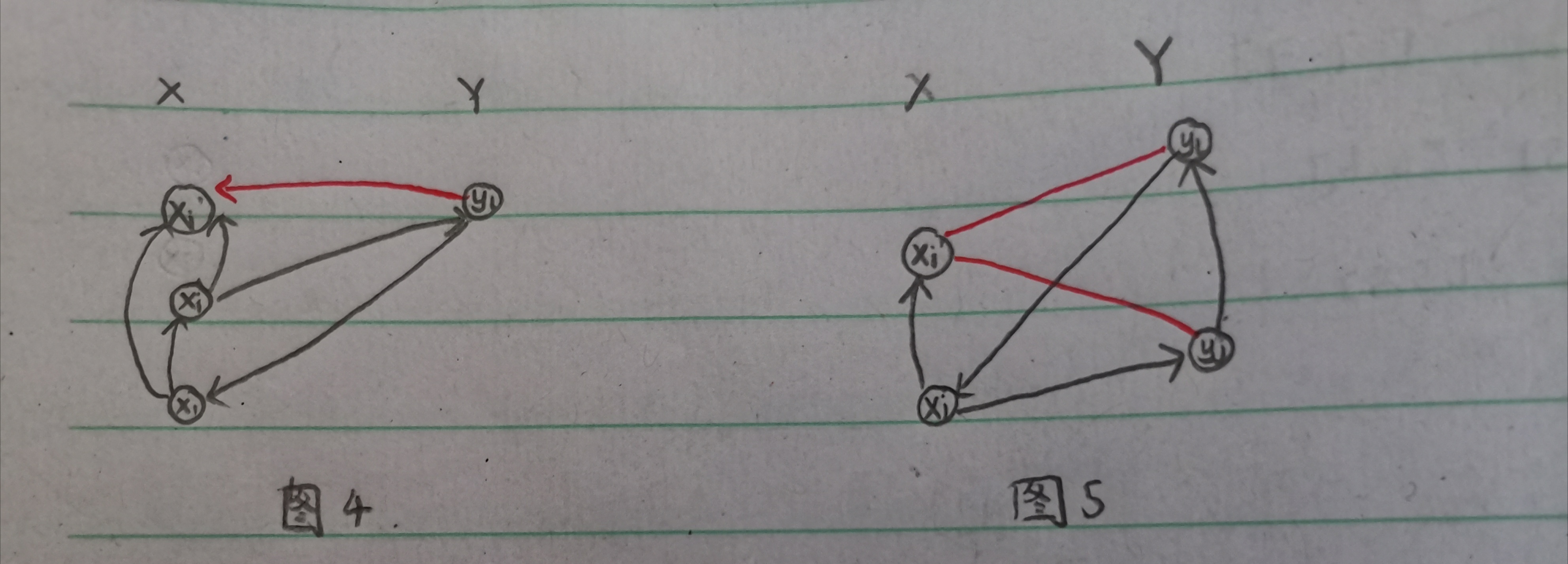
考虑一个(k imes l)的网格图,若存在(y_j o x_i),则将((i,j))涂黑.那么根据以上图的性质,可以得到这个网格图的某些性质
- 若((i,j))是黑色的,则对于所有(i'<i),((i',j))也是黑色的.
- 若((i,j))是黑色的,则对于所有(j'>j),((i,j'))也是黑色的.
- ((1,l))是黑色的.
- 对于所有(j),((k,j))是白色的.((v=x_k))
其中入度(le K)的条件相当于某个阶梯型的区域不能是黑色.
则方案数可以用一个(O(kl))的DP算出,令(v=1),枚举(|X|),(O(n)),(x_1,x_2,cdots,x_k,y_1,y_2,cdots y_l)的方案数可以最后乘以((n-1)!)表示,最初还要枚举删去的节点数.
总复杂度(O(n^4))
Code
https://atcoder.jp/contests/agc046/submissions/15081967
#include <cstdio>
#include <cstring>
#include <iostream>
#define debug(...) fprintf(stderr,__VA_ARGS__)
#define inver(a) power(a,mod-2)
using namespace std;
inline char gc() {
return getchar();
static char buf[100000],*l=buf,*r=buf;
return l==r&&(r=(l=buf)+fread(buf,1,100000,stdin),l==r)?EOF:*l++;
}
template<class T> void rd(T &x) {
x=0; int f=1,ch=gc();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=gc();}
while(ch>='0'&&ch<='9'){x=x*10-'0'+ch;ch=gc();}
x*=f;
}
typedef long long ll;
const int maxn=200+5;
int n,K,mod;
int fac[maxn],inv[maxn],C[maxn][maxn];
int dp[maxn][maxn];
inline int add(int x) {return x>=mod?x-mod:x;}
ll power(ll x,ll y) {
ll re=1;
while(y) {
if(y&1) re=re*x%mod;
x=x*x%mod;
y>>=1;
}
return re;
}
int sol(int k,int l,int K) {
memset(dp,0,sizeof(dp));
dp[0][0]=1;
for(int j=1;j<=l;++j) {
int sum=0;
for(int i=0;i<k;++i) {
sum=add(sum+dp[i][j-1]);
if((l-j+1)+(i-1)<=K&&(k-i)+(j-1)<=K) dp[i][j]=sum;
}
}
int an=0;
for(int i=1;i<k;++i) an=add(an+dp[i][l]);
return an;
}
int sol(int n,int K) {
if(n==1) return 1;
int an=0;
for(int i=1;i<=K+1;++i) an=add(an+sol(i,n-i,K));
an=(ll)an*fac[n-1]%mod;
// debug("%d %d %d
",n,K,an);
return an;
}
void init() {
fac[0]=1;
for(int i=1;i<=n;++i) fac[i]=(ll)fac[i-1]*i%mod;
inv[n]=inver(fac[n]);
for(int i=n;i>=1;--i) inv[i-1]=(ll)inv[i]*i%mod;
for(int i=0;i<=n;++i) {
C[i][0]=C[i][i]=1;
for(int j=1;j<i;++j) C[i][j]=add(C[i-1][j-1]+C[i-1][j]);
}
}
int main() {
rd(n),rd(K),rd(mod);
init();
int an=0;
for(int i=0;i<=K;++i) an=(an+(ll)sol(n-i,K-i)*C[n][i]%mod*fac[i])%mod;
printf("%d
",an);
return 0;
}