agc045_c Range Set
https://atcoder.jp/contests/agc045/tasks/agc045_c

Tutorial
https://img.atcoder.jp/agc045/editorial.pdf
考虑如何判断是否能得到某个01串
对于长度大于等于(A)的连续的0,可以把它看作1,这样变化后问题是等价的(最后将其染回0即可)
考虑在这样变换之后,如果存在一个长度大于等于(B)的连续的1,可以以它为中心按如下方式扩展
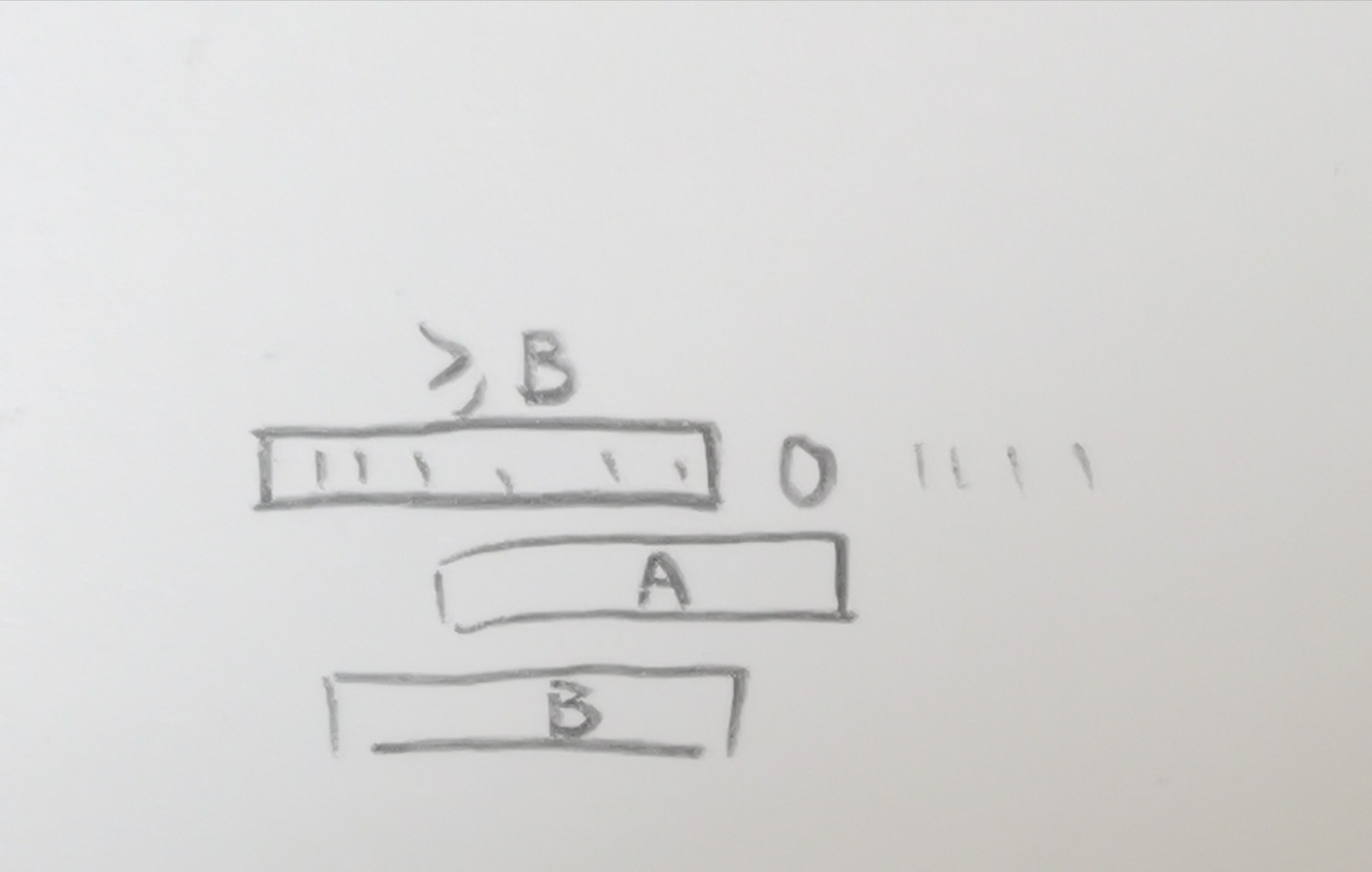
但是,考虑如果 (A>B) ,那么在边界的时候,这样的方法就有一点问题.
发现我们其实可以先将所有字符染为1,这样就得到了一个对称的问题.所以我们可以保证 (A le B) .
用DP统计满足上述条件的序列数即可
Code
#include <cstdio>
#include <iostream>
#define debug(...) fprintf(stderr,__VA_ARGS__)
#define upd(a,b) a=add(a+b)
using namespace std;
inline char nc() {
// return getchar();
static char buf[100000],*l=buf,*r=buf;
return l==r&&(r=(l=buf)+fread(buf,1,100000,stdin),l==r)?EOF:*l++;
}
template<class T> void read(T &x) {
x=0; int f=1,ch=nc();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=nc();}
while(ch>='0'&&ch<='9'){x=x*10-'0'+ch;ch=nc();}
x*=f;
}
typedef long long ll;
const int mod=1e9+7;
const int maxn=5000+5;
int n,A,B;
int f[maxn][2],g[maxn][2];
int dp[maxn][2][2];
inline int add(int x) {return x>=mod?x-mod:x;}
void DP(int dp[maxn][2]) {
for(int i=0;i<n;++i) {
upd(dp[i+1][1],dp[i][0]);
upd(dp[i+1][1],dp[i][1]);
for(int k=A;i+k<=n;++k) upd(dp[i+k][0],dp[i][1]);
}
}
int main() {
read(n),read(A),read(B);
if(A>B) swap(A,B);
f[0][0]=1,DP(f);
g[0][0]=1;
for(int i=A;i<=n;++i) g[i][0]=1;
DP(g);
dp[n][1][0]=g[n][0];
for(int i=1;i<=n;++i) dp[i][i>=B][1]=g[i][1];
for(int i=1;i<A;++i) dp[i][0][0]=1;
for(int i=1;i<=n;++i) for(int k=0;k<2;++k) {
for(int j=1;j<A&&i+j<=n;++j) upd(dp[i+j][k][0],dp[i][k][1]);
for(int j=1;i+j<=n;++j) {
int r=f[j][1]; if(i+j==n) upd(r,f[j][0]);
upd(dp[i+j][k||j>=B][1],(ll)dp[i][k][0]*r%mod);
}
}
printf("%d
",add(dp[n][1][0]+dp[n][1][1]));
return 0;
}