scipy包提供了几种通用的插补工具,分别用于1维,2维或高维的数据集,分别是:
- 类
interp1d用于对一维数据进行插补 - 类
griddata提供了对1D,2D和高维数据进行插补的工具。 - spline插补, 用于对一维和二维数据进行平滑的cubic-spline 插补
- 使用基于径向的函数(RBF)进行插值
这些方法都集成在scipy.interpolate模块中。
一,interp1d类
一维插补类(interp1d),是一种基于一维固定数据点创建函数的便捷方法,该函数内推一个一元的函数f,使得 y=f(x):
scipy.interpolate.interp1d(x, y, kind='linear', axis=-1, copy=True, bounds_error=None, fill_value=nan, assume_sorted=False)
kind 参数用于指定内推的类型,(‘linear’, ‘zero’, ‘slinear’, ‘quadratic’, ‘cubic’, ‘previous’, ‘next’和 ‘nearest’。对于'linear',是默认值,表示线性插补,前面已描述;对于 ‘zero’, ‘slinear’, ‘quadratic’ 和 ‘cubic’ 引用的是spline内推,使用 zeroth, first, second 和 third 顺序。对于 ‘previous’ 、 ‘next’ 和 ‘nearest’ 简单返回数据点的前一个、后一个或最近的一个数据。
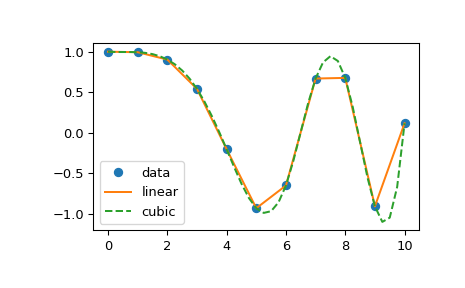
举个例子,使用interp1d内推两个函数,并绘制两个函数插补的数据点:
>>> import scipy >>> from scipy.interpolate import interp1d >>> x = np.linspace(0, 10, num=11, endpoint=True) >>> y = np.cos(-x**2/9.0) >>> f = interp1d(x, y) >>> f2 = interp1d(x, y, kind='cubic') >>> xnew = np.linspace(0, 10, num=41, endpoint=True) >>> import matplotlib.pyplot as plt >>> plt.plot(x, y, 'o', xnew, f(xnew), '-', xnew, f2(xnew), '--')>>> plt.legend(['data', 'linear', 'cubic'], loc='best') >>> plt.show()
二,多变量插补(griddata)
对于多维的数据,维度之间是相互关联的,例如,age、education和income是相互关联的,可以认为income = f(age,education)。对于二维数据,使用griddata 内推一个二元函数,z=f(x,y)。
scipy.interpolate.griddata(points, values, xi, method='linear', fill_value=nan, rescale=False)
参数注释:
- points:自变量,对于二元函数而言,points是指由(x,y)构成的数据点
- values:因变量,values是指某一个数据点的值,对于二元函数而言,数据点(x,y)的值是z=f(x,y)
- xi:坐标系,或者说是数据点在坐标系中的位置,也可以把points的值作为坐标系的x和y轴,把values作为坐标系的z轴
- method:有效值是‘linear’, ‘nearest’, ‘cubic’
三,spline类
一维spline的处理过程分为两个基本步骤:计算曲线的spline表示,对目标点进行评估。scipy有两种方式来计算曲线的spline表示和平滑系数:直接方式和参数化方式。
1,直接方式
直接方式使用splrep()函数从2维平面中查找曲线的spline表示,x和y是曲线在二维坐标系中的坐标。
splrep()函数的作用是对于给定数据点集(x [i],y [i]),确定在间隔xb <= x <= xe上平滑度为k的近似值。
scipy.interpolate.splrep(x, y, w=None, xb=None, xe=None, k=3, task=0, s=None, t=None, full_output=0, per=0, quiet=1)
参数注释:
- x和y定义一个曲线,y=f(x)
- w 权重,用于在spline拟合时计算加权最小二乘法的值,w的默认值为1/(len(x))。如果y值中的误差是向量d给出的标准偏差,则w应为1 / d。
- xb,xe:用于拟合的间隔,如果没有指定,那么默认值分别是x[0] 和 x[-1]。
- k 用于指定spline order,默认值是3,字符串表示为cubic,k的取值区间是[1,5]
- s 用于制定平滑条件,满足以下条件来确定平滑度:sum((w *(y-g))** 2,axis = 0)<= s,其中g(x)是(x,y)的平滑插值。 用户可以使用s来控制贴合度和平滑度之间的权衡,较大的s表示更平滑,而较小的s值表示较不平滑。s的推荐值取决于权重w。 如果权重代表y的标准偏差的倒数,则应在(m-sqrt(2 * m),m + sqrt(2 * m))范围内找到一个好的s值,其中m是 x,y和w中的数据点。 默认值:如果提供了权重,则s = m-sqrt(2 * m)。 如果未提供权重,则s = 0.0(内插)。
该函数输出的结果是一个三元组tck,这个三元组就是曲线的spline表示,用于表示曲线的节点向量、系数和spline序号,默认的spline orde是cubic,这可以通过k参数来修改。一旦确定了曲线的spline表示,就可以使用splev()函数对x进行评估:
scipy.interpolate.splev(x, tck, der=0, ext=0)
举个例子,使用splrep()函数来获取曲线的spline表示,也就是tck,再通过tck和splev()函数来评估曲线:
>>> import matplotlib.pyplot as plt >>> from scipy.interpolate import splev, splrep >>> x = np.linspace(0, 10, 10) >>> y = np.sin(x) >>> spl = splrep(x, y) >>> x2 = np.linspace(0, 10, 200) >>> y2 = splev(x2, spl) >>> plt.plot(x, y, 'o', x2, y2) >>> plt.show()

2,参数化方式
对于在N维空间中的区间,使用函数splprep()来定义曲线的参数:
scipy.interpolate.splprep(x, w=None, u=None, ub=None, ue=None, k=3, task=0, s=None, t=None, full_output=0, nest=None, per=0)
参数注释:
- x:代表N维空间中曲线的N个数组的列表,每个数组的长度都是曲线的点的数量,每一个数组都提供N维数据点的一个分量。
- u:是参数值的数组,该参数默认为0到1之间的等距单调序列,计算公式是:
M = len(x[0]), where v[0] = 0
v[i] = v[i-1] + distance(x[i], x[i-1])
u[i] = v[i] / v[M-1]
- ub,ue:参数间隔的端点,默认值是 u [0]和u [-1]。
- k:spline拟合的度,推荐使用默认值k=3,表示cubic,k的取值区间是[1,5]
- s:平滑度,是0到1之间的小数,0表示不平滑,值越大,平滑度越高。
- per:如果非0,那么把数据点视为周期性曲线,周期为x [m-1]-x [0],并返回平滑的周期样条近似。
默认输出包含两个对象:第一个对象是一个三元祖(t,c,k),分别表示曲线的节点向量、系数和spline序号;第二个对象是一个参数变量u。
对于函数splprep() 返回的spline表示,使用splev()函数来评估
>>> from scipy.interpolate import splprep, splev >>> tck, u = splprep([x, y], s=0) >>> new_points = splev(u, tck) >>> import matplotlib.pyplot as plt >>> fig, ax = plt.subplots() >>> ax.plot(x, y, 'ro') >>> ax.plot(new_points[0], new_points[1], 'r-') >>> plt.show()

参考文档: