【省选水题集Day1】一起来AK水题吧！ 题目（更新到B）

题解：http://www.cnblogs.com/ljc20020730/p/6937954.html 

水题A: [AHOI2001]质数和分解

题目网址： https://www.luogu.org/problem/show?pid=2563

题目描述

任何大于 1 的自然数 n 都可以写成若干个大于等于 2 且小于等于 n 的质数之和表达式(包括只有一个数构成的和表达式的情况)，并且可能有不止一种质数和的形式。例如，9 的质数和表达式就有四种本质不同的形式：

9 = 2 + 5 + 2 = 2 + 3 + 2 + 2 = 3 + 3 + 3 = 2 + 7 。

这里所谓两个本质相同的表达式是指可以通过交换其中一个表达式中参加和运算的各个数的位置而直接得到另一个表达式。

试编程求解自然数 n 可以写成多少种本质不同的质数和表达式。

输入输出格式

输入格式：

文件中的每一行存放一个自然数 n(2 < n < 200) 。

输出格式：

依次输出每一个自然数 n 的本质不同的质数和表达式的数目。

输入输出样例

输入样例#1：

2
200

输出样例#1：

1
9845164

2017-6-3 更新

水题B: [JSOI2008]完美的对称

 

题目描述

在峰会期间，必须使用许多保镖保卫参加会议的各国代表。代表们除了由他自己的随身保镖保护外，组委会还指派了一些其他的特工和阻击手保护他们。为了使他们的工作卓有成效，使被保卫的人的安全尽可能得到保障，保镖被分配到被保护人的各个方向。

保镖的最佳站立位置应该是这样的：被保护人应站在所有保镖的对称中心。但是，只要被保

护人一移动，保镖就很难根据要人的新位置调整位置。大多数的特工都很难对此作出实时调整。

因此，安全部长决定将该过程逆转一下，保镖先站好自己的位置，然后要人在他们的对称中心找到合适的位置。如果要人随便走动，我们就对他的安全不必负责。

你的工作是使这个过程自动操作。给出一组N个点（保镖的位置），你要找出它们的对称中心S，在这儿被保护人将相对安全。下面以此类推。

首先我们给定一点A以及对称中心S，点A'是点A以S为对称中心形成的像点，即点S是线段AA'的对称中心。

点阵组（X）以S为中心的像点是由每个点的像点组成的点阵组。X是用来产生对称中心S的，即点阵X以S为中心的像点的集合即为点阵X本身。

输入输出格式

输入格式：

输入文件第一行是一个整数N，1<=N<=20000，接下来的N行每行包含用空格隔开的两个整数Xi和Yi，-100000<=Xi,Yi<=100000，表示这组点阵中第I个点的笛卡尔坐标值。

因为任何两个保镖都不会站在同一个位置上，所以在给定的作业中，任何两点都不相同。但注意保镖可以站在被保护人相同的位置。

输出格式：

输出文件仅有一行。如果给定的点阵能产生一个对称中心，则输出“V.I.P. should stay at (x,y).”，其中X和Y代表中心的笛卡尔坐标值，格式为四舍五入保留至小数点后一位。

如果该组点阵无对称中心，输出"This is a dangerous situation!"，注意输出时除了两个单词之间用一个空格隔开外，不要输出多余空格。

输入输出样例

输入样例#1：

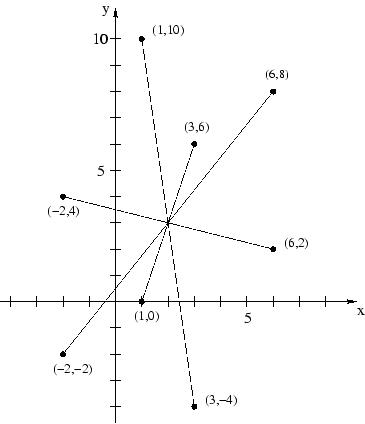
8
1 10
3 6
6 8
6 2
3 -4
1 0
-2 -2
-2 4

输出样例#1：

V.I.P. should stay at (2.0,3.0).

说明

[JSOI2008]第二轮

2017-6-9 更新