地址:https://ac.nowcoder.com/acm/contest/5667/C


题意:
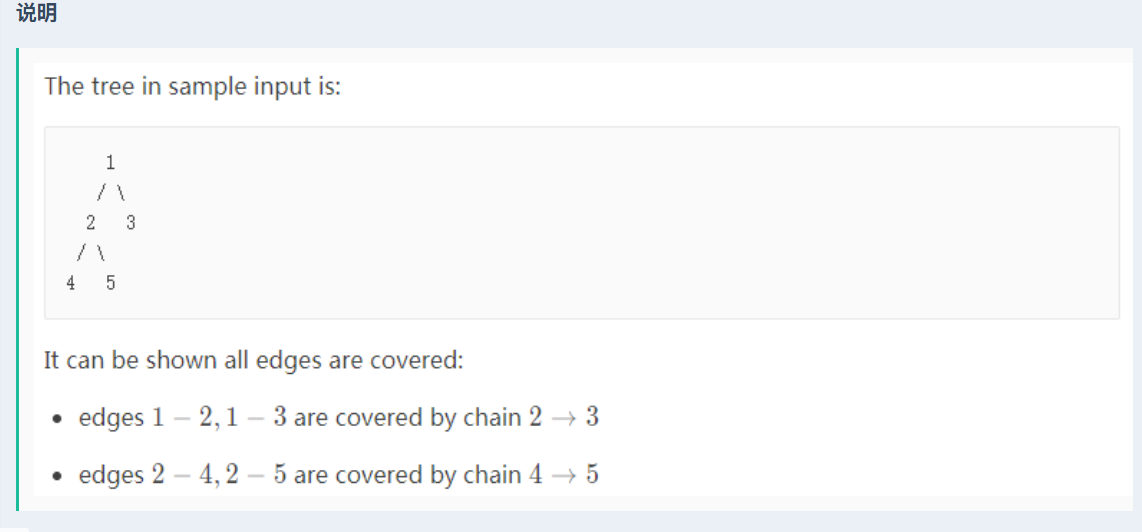
给定一个k个节点的无根树,求最少的链覆盖树上的所有边。并输出覆盖方式(链的两边的节点编号)
解析:
保证每一个边都有被覆盖,肯定与叶子节点有关系。
有结论:
用最少条链来覆盖一棵树的时候,最优解: (叶子结点数+1) / 2
对于叶子结点的求法,可以用vector建图,求叶子结点的dfs序:
dfs(i,-1); int dfs(int now,int fa)//fa防止走回头路! { if(v[now].size()==1) { a[tot++]=now; return 0; } for(int i=0;i<v[now].size();i++) { if(v[now][i]!=fa) { dfs(v[now][i],now); } } }
网上找的专业分析:

叶子结点:i与(i+sum/2)连接即可。
#include<bits/stdc++.h> typedef long long ll; using namespace std; const int maxn=2e5+20; vector<int>v[maxn]; int d[maxn],a[maxn]; int tot=1; int sum=0; int dfs(int now,int fa) { if(v[now].size()==1) { a[tot++]=now; return 0; } for(int i=0;i<v[now].size();i++) { if(v[now][i]!=fa) { dfs(v[now][i],now); } } } int main() { int n; cin>>n; for(int i=1;i<n;i++) { int a,b; cin>>a>>b; v[a].push_back(b); v[b].push_back(a); } for(int i=1;i<=n;i++) { if(v[i].size()>1) { dfs(i,-1); break; } } tot--; cout<<(tot+1)/2<<endl; for(int i=1;i<=(tot+1)/2;i++) cout<<a[i]<<" "<<a[i+tot/2]<<endl; }
不用dfs序的简单代码:
#include<bits/stdc++.h> typedef long long ll; using namespace std; const int maxn=2e5+20; int d[maxn],a[maxn]; int main() { int n; cin>>n; for(int i=1;i<n;i++) { int a,b; cin>>a>>b; d[a]++; d[b]++; } int sum=0; int tot=1; for(int i=1;i<=n;i++) { if(d[i]==1) a[tot++]=i,sum++; } cout<<(sum+1)/2<<endl; for(int i=1;i<=(sum+1)/2;i++) cout<<a[i]<<" "<<a[i+(sum)/2]<<endl; }