A 魔法部落
小Biu所在的部落是一个魔法部落,部落中一共有n+1个人,小Biu是魔法部落中最菜的,所以他的魔力值为1,魔法部落中n个人的魔法值都不相同,第一个人的魔法值是小Biu的3倍,第二个人的魔法值是第一个人的3倍,以此类推。
现在小Biu想知道整个部落的魔法值和是多少?由于答案比较大,请把答案对1e9+7取模之后输出。
输入
输入一个数N(0 <= N <= 10^9)
输出
输出:整个部落的魔法值和模1e9+7。
数据范围
对于20%的数据,n<=100; 对于40%的数据,n<=1000000; 对于100%的数据,n<=1000000000;
输入样例
3
输出样例
40
样例解释
3^0+3^1+3^2+3^3 = 1+3+9+27 = 40
题意如此,此为等比数列,根据等比求和公式,为(3^(n+1)-1)/2 mod1e9+7
由于n很大,做除数再取模会损失精度,所以我们需要把他转化为乘法来计算。那么就用到了逆元思想。
逆元:方程 的解称为
关于模
的逆,意思也为:ax%p==1。当
(即
,
互质)时,方程有唯一解,否则无解。
x为a关于p的逆元。
我们把式子写成(a/b)%m,推理过程如下,字迹潦草,勿怪
 即我们需要求(a*c)mod m。c为b的逆元。
即我们需要求(a*c)mod m。c为b的逆元。
费马小定理:当 为质数时,有
,那么易得出
。
根据题意,mod=1e9+7,即为p的位置,mod为质数,适用于费马小定理求逆元,c的位置即为b^(p-2)的位置,这样根据b求c就可以了。。b=2,则求2^(mod-2),利用快速幂来求
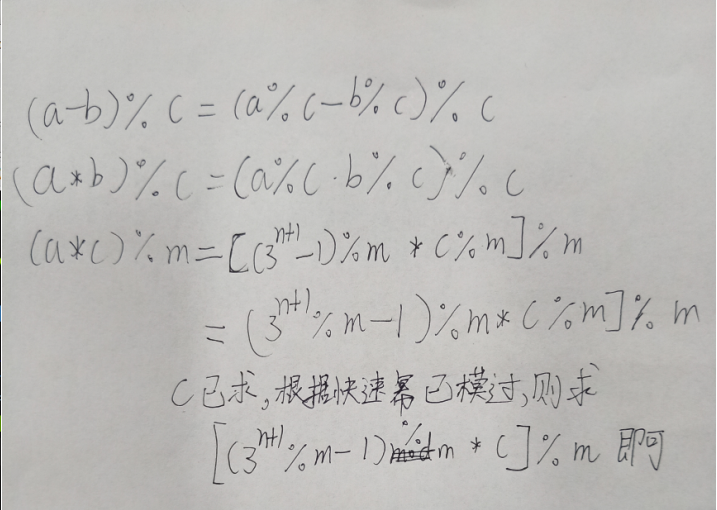
上代码:
#include<iostream> using namespace std; typedef long long ll; const int mod=1e9+7; int qk(ll a, ll b) { ll ans=1; a=a%mod; while(b) { if(b%2==1) ans=(ans*a)%mod; b=b/2; a=(a*a)%mod; } return ans; } int main(){ ll n; while(cin>>n) { ll c=qk(2,mod-2); ll zi=qk(3,n+1)-1; cout<<(zi%mod*c)%mod<<endl; } }
一个队友给的优化,直接快速幂 ,模的时候mod*2即可,排除了结果为5e8的情况,那样会出现精度丢失...