摘要
图神经网络已成为解决图结构数据机器学习问题的重要技术之一。最近关于顶点分类的工作提出了深度和分布式学习模型,以实现高性能和可扩展性。然而,我们发现基准数据集的特征向量已经为分类任务提供了相当多的信息,而图结构仅仅提供了一种对数据进行去噪的方法。本文提出了一种基于图信号处理的分析图神经网络的理论框架。结果表明,图神经网络仅对特征向量进行低通滤波,不具有非线性流形学习特性。我们进一步研究了它们对特征噪声的抵抗能力,并对基于GCN的图形神经网络设计提出了一些见解。
1 介绍
图形神经网络(GNN)是一类能够从图形结构数据中学习的神经网络。近年来,用于顶点分类和图同构检验的图神经网络在多个基准数据集上取得了良好的效果,并不断创造出新的性能水平[1,16,26,29]。从ChebNet[6]和GCN[16]在顶点分类方面的早期成功开始,GNN的许多变体被提出用于解决社交网络[12,31]、生物学[26,27]、化学[8,10]、自然语言处理[2,32]、计算机视觉[21]和弱监督学习[9]中的问题。
在半监督顶点分类中,我们观察到图卷积网络(GCN)[16]中图卷积层的参数只会导致过度拟合。在SGC[28]等简单架构和DGI[27]等更复杂架构中都报告了类似的观察结果。基于这种现象,吴等人。[28]提出将图神经网络简单地看作是特征传播,并提出了一个在许多基准数据集上具有最新性能的极为有效的模型。川本等人。[14] 对图分区设置下未训练的类GCN GNNs作了相关的理论评述。从这些先前的研究中,一个问题自然而然地出现了:为什么图神经网络在顶点分类方面工作得很好,什么时候工作得很好?换言之,图神经网络模型的顶点特征向量是否有条件即使不经过训练也能正常工作?因此,我们能否找到基线图神经网络(如SGC或GCN)无法执行的现实反例?
在本研究中,我们从图形信号处理的角度回答了上述问题[19]。形式上,我们考虑图上的半监督学习问题。
给定一个图G=(V,E),每个顶点i∈V有一个特征x(i)∈X和标记y(i)∈Y,其中X是一个d维欧氏空间,每个顶点i可以用其特征x(i)来表示,并且和其标记y(i)相关联。Y用于回归,Y={1,...,c}用于分类。任务是学习从特征x(i)预测标签y(i)的一个假设空间,这个就是一个分类问题。本文用图神经网络解决了这个分类问题,gnn的节点分类问题就是:给定部分标记y的图G,目标是利用这些标记的节点来预测未标记的节点标签,它通过学习得到每个节点的k维向量(状态)表示为h(i),同时包含其相邻节点的信息。并为最常用的基线模型GCN[16]及其简化变体SGC[28]的机制提供了见解。
图形信号处理(GSP)将顶点上的数据作为信号,应用信号处理技术来理解信号的特征。通过将信号(特征向量)和图结构(邻接矩阵或其变换)相结合,GSP启发了图结构数据学习算法的发展[23]。在标准信号处理问题中,通常假设观测值包含一些噪声,而潜在的“真实信号”具有低频率[20]。在这里,我们对我们的问题提出了类似的假设。
假设1:输入特征包括低频真实特征和噪声。真实特征对于机器学习任务具有足够的信息。
我们的第一个贡献是在常用数据集上验证假设1(第3节)。下图显示了两层感知器(MLP)在不同频率分量的特征上训练的性能。在所有基准数据集中,我们看到只有少数频率成分有助于学习。在特征向量中加入更多的频率分量只会降低性能。当特征中加入高斯噪声N(0,σ2)时,分类精度进一步降低。
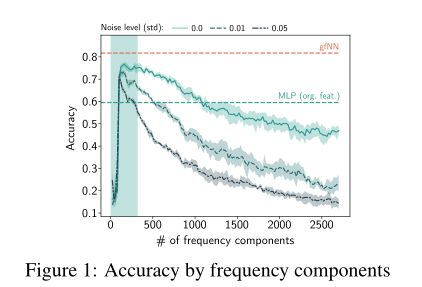
这个图说明了两件事:噪声的存在会降低分类准确率,这个显然;然后特征分得越细越多不一定越好,因为只有少数的特征会帮助我们提高分类准确率,多了反而下降,有点像过拟合。
许多最新的gnn是建立在图形信号处理的结果之上的。最常见的做法是将(增广的)标准化邻接矩阵I(邻接矩阵的定义)与特征矩阵X相乘。乘积被理解为特征平均和传播[12、16、28]。在图信号处理文献中,这种操作在图上过滤信号,而不是显式地对归一化拉普拉斯矩阵执行特征分解,这需要O(n3)时间。在这里,我们将这个扩充的规范化邻接矩阵及其变体称为图滤波器和传播矩阵。
我们的第二个贡献表明,将图信号与传播矩阵相乘对应于低通滤波(第4节,特别是定理3)。此外,我们还证明了观测信号和低通滤波器之间的矩阵积是真实信号优化问题的解析解。与图神经网络的最新设计原理[1,16,29]相比,我们的结果表明图卷积层是简单的低通滤波。因此,不必学习图卷积层的参数。吴等人。[28,定理1]还通过分析增强规范化邻接矩阵的谱截断效应来解决类似的问题。我们将这一结果推广到所有特征值单调收缩,进一步解释了谱截断效应的含义。
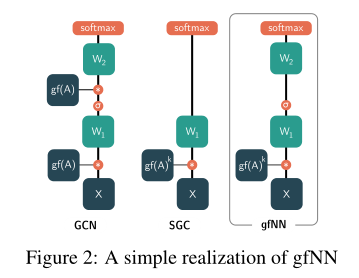
在理论分析的基础上,我们提出了一个新的基线框架gfNN(graph filter neural network)来实证分析顶点分类问题。gfNN包括两个步骤:1。用图过滤矩阵相乘的方法过滤特征。利用机器学习模型学习顶点标签。我们使用下图中的一个简单实现模型来演示我们的框架的有效性。
2 图信号处理
一些基本定义:
定义一个简单无向图,称为$G(V,varepsilon )$,$V$代表顶点的集合,$varepsilon $代表边的集合,假设图G中有n个节点。定义$A=(a_{ij})in mathbb{R}^{n imes n}$为邻接矩阵,邻接矩阵的含义在有向无环图中的定义就是$A$中元素$a_{ij}$在节点$i$和$j$有连线的时候为1,其余时候为0,所以$A$是一个对角线上为0的对称矩阵。
然后定义$G$的度矩阵,度就是一个节点上由几条边,度在图用于研究社交网络的时候可以用作衡量一个节点的影响力,当然衡量节点影响力也有其他的方法。G的度矩阵就是把各个节点的度放在矩阵的对角线位置,所以定义如下:$D=diag(d(1),..d(n))in mathbb{R}^{n imes n}$,其中$d(i)=sum_{jin V}^{ }a_{ij}$
此时,我们让$L=D-A$,也就是定义一个新的矩阵$L$,它是用图$G$的度矩阵$D$减去邻接矩阵$A$,因为我们知道$A$的对角线上元素都为0,其余位置有可能是0或1;而$D$是其余位置为0,只有对角线上元素有可能为正数。故$L$就是一个对角线上元素为度,其余位置为0或-1的一个矩阵。我们称$L$为组合拉普拉斯矩阵(combinatorial Laplacian)
然后定义$L =I-D^{-frac{1}{2}}AD^{-frac{1}{2}}$,其中I是一个单位阵,称$L $为标准拉普拉斯矩阵(normalized Laplacian)
定义$L_{rw}=I-D^{-1}A$,为随机游走拉普拉斯矩阵(random walk Laplacian)
接下来我们考虑增加自循环:
定义$widetilde{A}=A+gamma I$,为增强邻接矩阵,也就是给每个节点加上了一个自循环,在最开始因为$G$是一个简单无向图,简单就蕴含着无环,所以$A$的对角线元素上为0,现在增加了一个$gamma$就是给A的每个节点都增加了一个“自己到自己的连接”;相应的每个节点增加了自循环的线条,所以度也要跟着改变为$widetilde{D}=D+gamma I$,它是相应的增强度矩阵;同时三个拉普拉斯矩阵也随着变化,当然$L=D-A=widetilde{L}$组合拉普拉斯是不变的,因为$A$和$D$只是对角线元素上同时增加了,相减时依旧为0;标准拉普拉斯变为$widetilde{L } =I-widetilde{D^{-frac{1}{2}}}widetilde{A}widetilde{D^{-frac{1}{2}}}$,就是把$A$用$widetilde{A}$替换,$D$用$widetilde{D}$替换而已;随机游走拉普拉斯变为$widetilde{L_{rw}}=I-widetilde{D^{-1}}widetilde{A}$
在图的顶点上定义的向量x∈rn称为图信号。为了引入图的傅里叶变换,我们需要在图信号的空间上定义两个运算:变分variation$Delta x$和内积inner product。

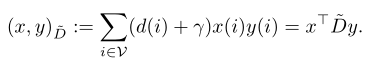
所以图信号的变分其实就是两两节点之间的差值。内积就是用单个节点的度(影响力)乘上它的信息$x(i)$以及标签,然后所有节点累加。
变分描述了怎么样测量一个信号的平滑性smoothness,而内积描述了怎么样测量一个信号的重要性,内积更加关注那些度很高的节点,而$gamma$的存在使得内积可以相对公平一点,不那么着眼于度。
然后我们考虑广义特征值问题(变分形式):
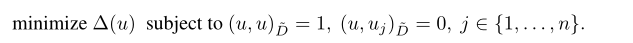
我们要找到一组$u_{1},u_{2},..u_{n}$使得上式成立,这组解也是下述式子的解:
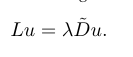
其中$u_{i}是广义特征向量,而对应的$lambda (i)$是广义特征值。具有较小广义特征值的广义特征向量就变化而言更平滑。因此,广义特征值被称为图的频率 frequency of the graph。
傅里叶部分先跳过,因为还没看懂,反正傅里叶变换就是把特征x(i)经过了某种变换成新的向量,把一个函数变换成一系列正交函数的组合(sin,cos)叠加。

在一个图的机器学习问题中,每个顶点i∈V都有一个d维特征x(i),我们把这些特征看作图信号,通过每个信号的图傅里叶变换定义特征的图傅里叶变换。设X=[x(1),...,x(n)]是特征矩阵。然后,经过傅里叶变换我们表示widehat{X}=[widehat{x}(lambda _{1}),widehat{x}(lambda _{2}),...,widehat{x}(lambda _{n}),]>作为X的频率分量。
3
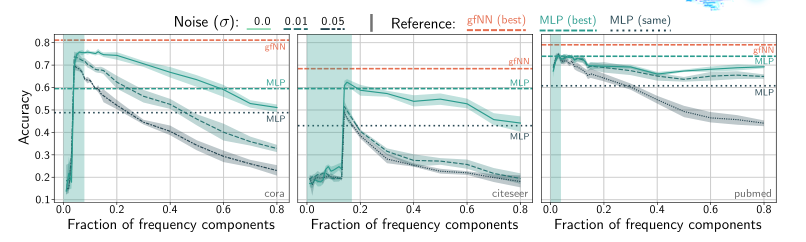
在上图中,我们递增地添加标准化的拉普拉斯频率分量来重建特征向量并训练2层mlp。我们看到这三个数据集都表现出低频特性(?)。两层MLP的分类精度往往在光谱的前20%内达到峰值。通过加入人工高斯噪声,我们观察到在低频区域的性能是相对稳健的,准确率上升基本没有什么变化,这意味着较强的去噪效果。
图中表示2层MLPs在频率受限特征向量(epoch=20)上的平均性能。红线gfNN(best)和绿线MLP(best)显示了使用gfNN的最佳性能,和基于原始特征训练的2层MLP的最佳性能。
有趣的是,当高频成分不包含有用的分类信息时,图神经网络和简单MLP之间的性能差距要大得多。在Cora数据集中,高频成分只会降低分类精度。因此,我们的gfNN优于简单的MLP。citeeser和Pubmed具有类似的低频特性。然而,这里的性能差距并没有那么大。由于citeeser和Pubmed的加噪性能线的行为通常类似于原始Cora性能线,因此我们希望原始citeeser和Pubmed包含的噪声比Cora少很多。因此,我们可以期望图的过滤度在城市和公共场合几乎没有影响。
4
由于计算拉普拉斯矩阵的特征值分解需要O(| V | 3)时间,因此计算低频分量非常昂贵。因此,合理的替代方案是使用低通滤波器。关于图神经网络的许多文献都是通过迭代乘法(增广)邻接矩阵Arw(或A)来传播信息。在本节中,我们看到这个操作对应于一个低通滤波器。