<<信息学奥赛一本通>> 过河卒

1314：【例3.6】过河卒(Noip2002)

时间限制: 1000 ms         内存限制: 65536 KB
提交数: 4212     通过数: 1741 

【题目描述】

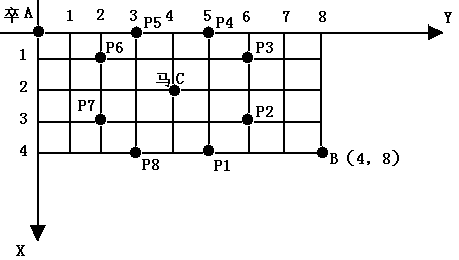
棋盘上A点有一个过河卒，需要走到目标B点。卒行走的规则：可以向下、或者向右。同时在棋盘上的某一点有一个对方的马（如C点），该马所在的点和所有跳跃一步可达的点称为对方马的控制点，如图3-1中的C点和P1，……，P8，卒不能通过对方马的控制点。棋盘用坐标表示，A点(0,0)、B点(n, m) (n,m为不超过20的整数),同样马的位置坐标是需要给出的，C≠A且C≠B。现在要求你计算出卒从A点能够到达B点的路径的条数。

【输入】

给出n、m和C点的坐标。

【输出】

从A点能够到达B点的路径的条数。

【输入样例】

8 6 0 4

【输出样例】

1617

公式好推.

数组出界问题，
(1) 我是在外面多加了一圈。

不过看了下 LG 的题解，
原来可以用 三目运算符 来保证不出界
(2) a[i == 0 ? i : i-1][j] 

马的控制点判断 
(1) 可以用数组[][] 当地图，把有马控制的地方变为1 来判断，(用空间换时间)。
(2) (i==mx+1||i==mx-1)&&(k==my+2||k==my-2)  (i,j) 为 终点, (mx,my) 马所处的位置。

自己写的:

#include<iostream>
using namespace std;

    int n,m,cx,cy;
    long long step[25][25] = {0};
    int h[9][2];
    int insX[] = {2,2,-2,-2,1,1,-1,-1},
        insY[] = {1,-1,1,-1,2,-2,2,-2};
    bool flag = false;
    
int main() {
    
    cin >> n >> m >> cx >> cy;
    //HORSE
    h[0][0] = cx+1,h[0][1] = cy+1;
    for(int i=0;i<8;i++){
        h[i+1][0] = h[0][0] + insX[i];
        h[i+1][1] = h[0][1] + insY[i];    
    }
    //STEP
    step[1][1]=1;
    
    for(int i=1; i<= n+1; ++i) {
        for(int j=1; j<= m+1; ++j) {
            if( i!=1 || j!=1){
                for(int k=0;k<9;++k){
                    if(i==h[k][0] && j==h[k][1]){
                        flag = true;
                    }
                }
                if(!flag){
                    step[i][j] = step[i-1][j] + step[i][j-1];
                }
                flag = false;                
            }
        }
    }
    
    cout << step[n+1][m+1] << endl;
}

 解法二

#include <iostream>
using namespace std;
int dir[8][2] = {{1, 2}, {1, -2}, {2, 1}, {2, -1}, {-1, 2}, {-1, -2}, {-2, 1}, {-2, -1}};
bool d[30][30];
long long dp[30][30];
int main() {
    int n, m, cx, cy;
    // n, m 是棋盘大小，cx, cy 是马的位置
    cin >> n >> m >> cx >> cy;
    d[cx][cy] = true;
    for(int i=0;i<8;i++){
        int tx = cx + dir[i][0];
        int ty = cy + dir[i][1];
        if(tx>=0 && tx<=n && ty>=0 && ty<=m){
            d[tx][ty] = true;
        }
    }
    dp[0][0] = 1;
    for(int i=0;i<=n;i++){
        for(int j=0;j<=m;j++){
            if(d[i][j] == false){
                if(i){
                    dp[i][j] += dp[i-1][j];
                }
                if(j){
                    dp[i][j] += dp[i][j-1];
                }
            }
        }
    }
    cout << dp[n][m] << endl;
    return 0;
}