平面最小点对距:分治法
时间:2020.03.21
地点:深圳
语言:C#
IDE: VS2019
概述:用分治法求平面内离散的点求最小点对距
1. 分治法

语言实现详细步骤:
1、设计点对距数据结构{点距,起点,终点}
2、从txt读取点集合
3、点集合排序
4、获取中点索引,划分左右区域
5、左右区域求最小点对距
6、比较左右区域最小点对距,选取最小值作为中线缓冲距离
7、获取缓冲区点集合
8、缓冲区点集合求最小点对距
9、比较左、中、右点对距,选择最小点对距
PointPairDis.cs
using System;
namespace 点线面
{
public partial class PointPairDis
{
#region 字段属性
private double distance;
private Point pointFrom;
private Point pointTo;
public double Distance { get => distance; set => distance = value; }
public Point PointFrom { get => pointFrom; set => pointFrom = value; }
public Point PointTo { get => pointTo; set => pointTo = value; }
#endregion
#region 方法
public void WriteLine()
{
Console.WriteLine("{0} {1} {2} ",
Distance, PointFrom.PointName, PointTo.PointName);
Console.WriteLine("-----------------------");
}
public void MinPointPairDis(Points points)
{
#region 变量
int startIndex;
int midIndex;
int endIndex;
double buffer;
PointPairDis pointPairDis_left = null;
PointPairDis pointPairDis_mid = null;
PointPairDis pointPairDis_right = null;
#endregion
//排序
points.SortPoints();
//获取中线缓冲距离
points.GetIntervalIndex(out startIndex, out midIndex, out endIndex);
pointPairDis_left =points.GetMinPointsDis(startIndex, midIndex);
pointPairDis_right =points.GetMinPointsDis(midIndex, endIndex);
if (pointPairDis_left.Distance < pointPairDis_right.Distance)
buffer = pointPairDis_left.Distance;
else
buffer = pointPairDis_right.Distance;
//获取中线区域最小点对距
points.GetIntervalIndex(out startIndex, out midIndex, out endIndex, buffer);
pointPairDis_mid =points.GetMinPointsDis(startIndex, endIndex);
//最小点对距
if (pointPairDis_left.Distance < pointPairDis_right.Distance)
{
if (pointPairDis_mid.Distance < pointPairDis_left.Distance)
pointPairDis_mid.WriteLine();
else
pointPairDis_left.WriteLine();
}
else
{
if (pointPairDis_mid.Distance < pointPairDis_right.Distance)
pointPairDis_mid.WriteLine();
else
pointPairDis_right.WriteLine();
}
}
#endregion
}
}
Points类内的方法:
#region 最小点对距
public void SortPoints()
{
pointList.Sort(new ComparerPoints());
}
public void GetIntervalIndex(out int startIndex, out int midIndex,
out int endIndex, double buffer = 0)
{
startIndex = 0;
endIndex = pointList.Count - 1;
if (pointList.Count % 2 == 0)
midIndex = pointList.Count / 2;
else
midIndex = (pointList.Count + 1) / 2; ;
if (buffer != 0)
{
//左缓冲
for (int i = 1; i < midIndex; i++)
{
double disLeft2Xmiddle = pointList[midIndex].PointX
- pointList[midIndex - i].PointX;
if (disLeft2Xmiddle >= buffer)
{
startIndex = midIndex - i;
break;
}
}
//右缓冲
for (int i = 1; i < midIndex; i++)
{
double disRigth2Xmiddle = pointList[midIndex + i].PointX
- pointList[midIndex].PointX;
if (disRigth2Xmiddle >= buffer)
{
endIndex = midIndex + i;
break;
}
}
}
}
/// <summary>
/// 获取区间范围最小点对距
/// </summary>
/// <param name="start">起点索引</param>
/// <param name="end">终点索引</param>
/// <returns>点对距</returns>
/// <remarks>20200318 刘小贝</remarks>
public PointPairDis GetMinPointsDis(int start, int end)
{
PointPairDis pointPairDis = new PointPairDis
{
Distance = pointList[start].Distance2Point(pointList[start + 1]),
PointFrom = pointList[start],
PointTo = pointList[start + 1]
};
for (int i = start; i < end; i++)
{
for (int j = i + 1; j <= end; j++)
{
double dis = pointList[i].Distance2Point(pointList[j]);
if (dis < pointPairDis.Distance)
{
pointPairDis.Distance = dis;
pointPairDis.PointFrom = pointList[i];
pointPairDis.PointTo = pointList[j];
}
}
}
return pointPairDis;
}
#endregion
IComparer接口实现:
public class ComparerPoints : IComparer<Point>
{
int IComparer<Point>.Compare(Point x, Point y)
{
if (x.GetPointX() < y.GetPointX())
{
return -1;
}
else
return 1;
}
}
运行结果为:
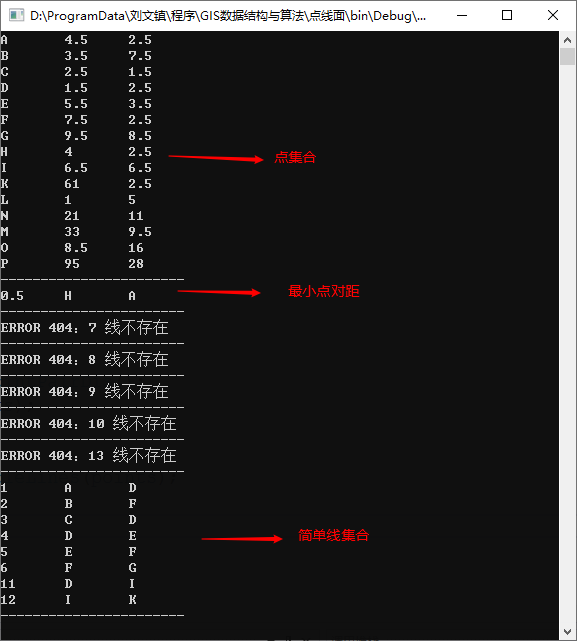
2. 旋转法
(1)以横坐标为关键字,将点的坐标排序
(2)把坐标轴旋转任意角度
(3)以横坐标为关键字,将n点的坐标排序
这是数学上的旋转公式
x1=x*cos(ds)-y*sin(ds);
y1=x*sin(ds)+y*cos(ds);
代码为:
作者:硝基苯张
链接:https://zhuanlan.zhihu.com/p/77472546
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cmath>
#include<ctime>
#include<cstdlib>
#define db double
#define ll unsigned long long
using namespace std;
int n;db ans=4e20;
struct E{
db x,y;
}a[200001];
bool cmp(E t1,E t2)
{
return t1.x<t2.x;
}
db minn(db a,db b)
{
if(a<b)return a;
else return b;
}
void dfs(int x)
{
for(int i=x+1;i<=min(x+5,n);i++)
{
if(a[i].x-a[x].x>=ans)break;
ans=minn(ans,(a[x].x-a[i].x)*(a[x].x-a[i].x)+(a[x].y-a[i].y)*(a[x].y-a[i].y));
}
//cout<<ans<<endl;
}
void around(int ds)
{
for(int i=1;i<=n;i++)
{
db x=a[i].x,y=a[i].y;
a[i].x=x*cos(ds)-y*sin(ds);
a[i].y=x*sin(ds)+y*cos(ds);
}
sort(a+1,a+1+n,cmp);
}
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
scanf("%lf%lf",&a[i].x,&a[i].y);
sort(a+1,a+1+n,cmp);
for(int i=1;i<n;i++)dfs(i);
around((rand()+1)%360-1);
for(int i=1;i<n;i++)dfs(i);
around(rand()%360);
for(int i=1;i<n;i++)dfs(i);
printf("%.4lf",sqrt(ans));
}
来源:知乎:硝基苯张
其他参考:洛谷算法