Write a program to find the nth super ugly number.
Super ugly numbers are positive numbers whose all prime factors are in the given prime list primes of size k. For example, [1, 2, 4, 7, 8, 13, 14, 16, 19, 26, 28, 32] is the sequence of the first 12 super ugly numbers given primes = [2, 7, 13, 19] of size 4.
Note:
(1) 1 is a super ugly number for any given primes.
(2) The given numbers in primes are in ascending order.
(3) 0 < k ≤ 100, 0 < n ≤ 106, 0 < primes[i] < 1000.
【题目分析】
在之前ugly number题目的基础上,这个题目在primes数上进行了扩充,不只是之前的2,3,5这三个数,而是可以以一个增序的序列给出k个质数。在这个基础上求出第n个ugly number。
【思路】
与之前的思路相同,我们为每一个prime维持一个指针指向i,表示第i次的ugly number与该prime相乘的结果作为下一个ugly number的候选值。每次我们取这些候选值中最小的,因此每个prime的指针指向的数与该prime相乘都会大于当前最后一个ugly number。当某些指针指向的数与当前prime相乘是最小的话,该prime指针向后移动一位。
一个例子如下:primes = [2,3,5], n = 7
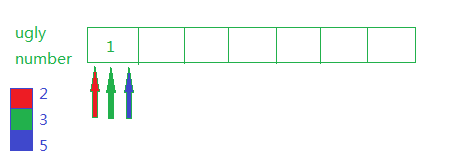
1. 初始第一个ugly number是1,三个指针都指向1.
比较1*2,1*3,1*5的大小,取最小值,并且对应的指针向后移动,结果如下:
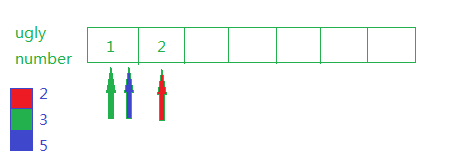
2. 第二个ugly number是2。比较1*3,1*5和2*2的大小取最小值,对应指针向后移动,结果如下:
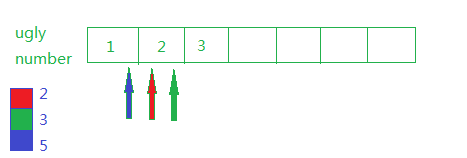
3. 第三个ugly number是3。比较1*5,2*3和2*2的大小取最小值,对应指针向后移动,结果如下:
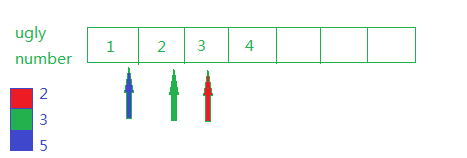
4. 第四个ugly number是4。比较1*5,2*3和3*2的大小取最小值,对应指针向后移动,结果如下:
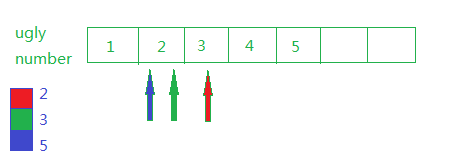
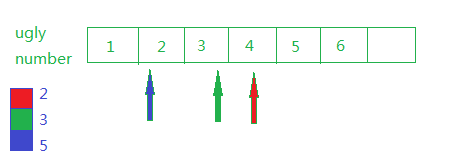
以此类推,结果如下:
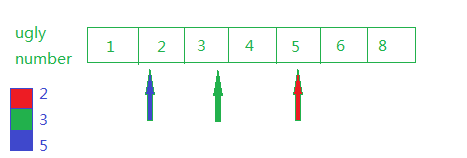
【java代码】
1 public class Solution { 2 public int nthSuperUglyNumber(int n, int[] primes) { 3 int[] pointerN = new int[primes.length]; 4 int[] num = new int[n]; 5 num[0] = 1; 6 7 for(int i = 1; i < n; i++) { 8 int min = Integer.MAX_VALUE; 9 for(int j = 0; j < primes.length; j++) { 10 int curnum = primes[j] * num[pointerN[j]]; 11 if(curnum < min) min = curnum; 12 } 13 num[i] = min; 14 for(int j = 0; j < pointerN.length; j++) { 15 int curnum = primes[j] * num[pointerN[j]]; 16 if(curnum == min) pointerN[j]++; 17 } 18 } 19 return num[n-1]; 20 } 21 }