R语言中计算协方差、相关系数。

001、

1.协方差

方差是描述自身偏离其均值的程度。

协方差用来描述两个变量间的变化关系,协方差用来度量两个随机变量关系的统计量：

<span class="mrow"><span class="mi"><img src="https://img2022.cnblogs.com/blog/1447599/202207/1447599-20220731123105542-380290930.png" alt="" loading="lazy" /> <span class="mrow"><span class="mi">

E[x] 代表期望，一般置X的均值。

公式：如果有X,Y两个变量，每个时刻的“X值与其均值之差”乘以“Y值与其均值之差”得到一个乘积，再对这每时刻的乘积求和并求出均值。

总结一下，如果协方差为正，说明X，Y同向变化，协方差越大说明同向程度越高；如果协方差为负，说明X，Y反向运动，协方差越小说明反向程度越高。

dat1 <- c(2, 4, 6, 4)
dat2 <- c(8, 10, 6, 12)
cov(dat1, dat2)

mean1 <- mean(dat1)
mean2 <- mean(dat2)

mean2

sum <- 0
for (i in 1:4) {
  sum = sum + (dat1[i] - mean1) * (dat2[i] - mean2)
}
sum
sum/(4 - 1)

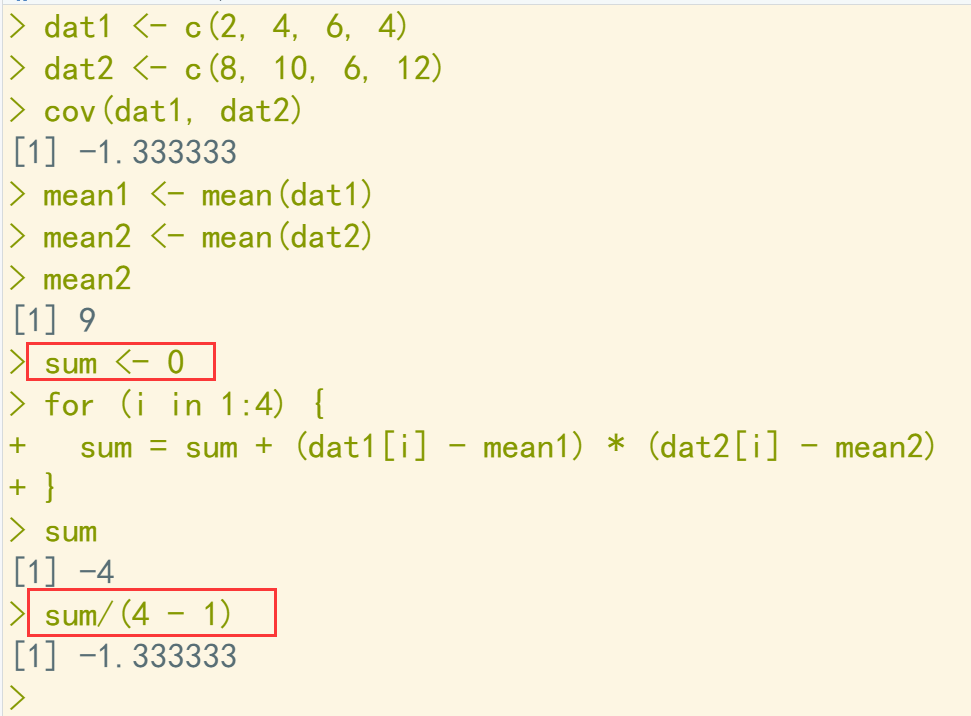
2、相关系数

协方差除以标准差的乘积。

就是用X、Y的协方差除以X的标准差和Y的标准差。

所以，相关系数也可以看成协方差：一种剔除了两个变量量纲影响、标准化后的特殊协方差。

既然是一种特殊的协方差，那它：

1、也可以反映两个变量变化时是同向还是反向，如果同向变化就为正，反向变化就为负。

2、由于它是标准化后的协方差，因此更重要的特性来了：它消除了两个变量变化幅度的影响，而只是单纯反应两个变量每单位变化时的相似程度。

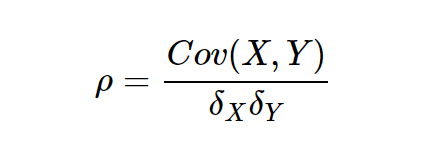
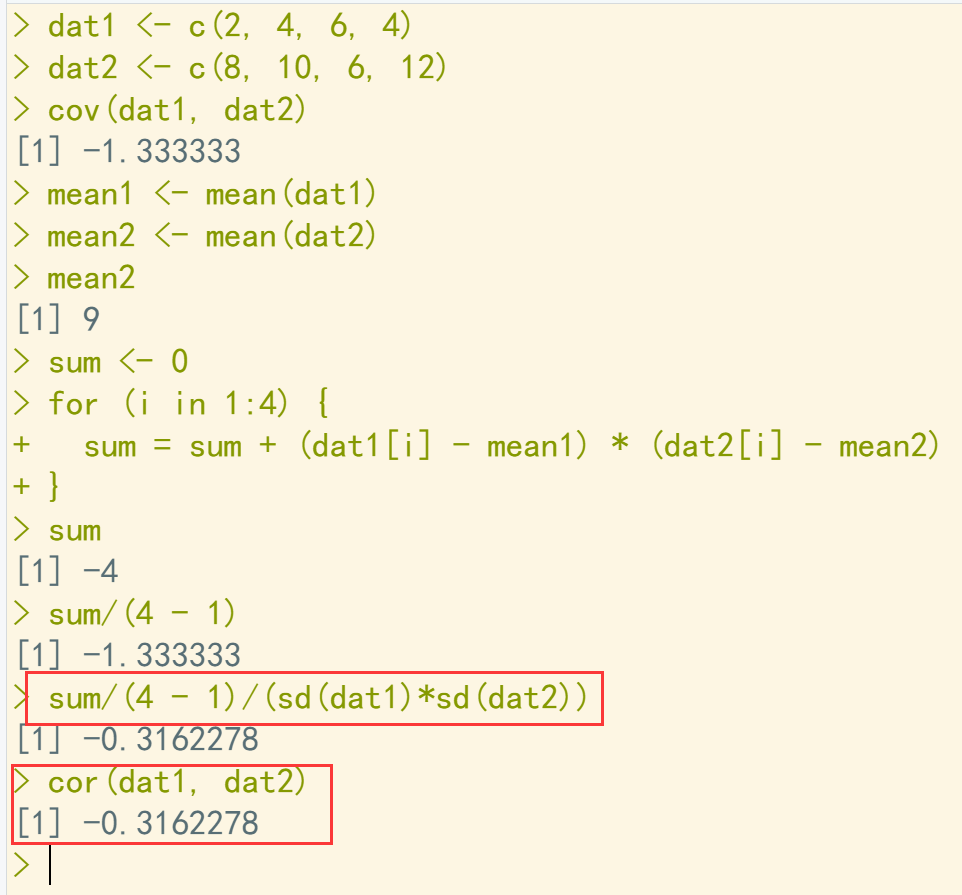
dat1 <- c(2, 4, 6, 4)
dat2 <- c(8, 10, 6, 12)
cov(dat1, dat2)

mean1 <- mean(dat1)
mean2 <- mean(dat2)

mean2
sum <- 0
for (i in 1:4) {
  sum = sum + (dat1[i] - mean1) * (dat2[i] - mean2)
}
sum
sum/(4 - 1)                          ## 协方差，方向两个变量同向或反向变化。

sum/(4 - 1)/(sd(dat1)*sd(dat2))      ## 相关系数 = 协方差除以标准差的乘积。
cor(dat1, dat2)

 

参考：https://www.zhihu.com/question/20852004