传送门
题面:
C. Rectangles
time limit per test
2 seconds
memory limit per test
256 megabytes
input
standard input
output
standard output
You are given nn rectangles on a plane with coordinates of their bottom left and upper right points. Some (n−1)(n−1) of the given nn rectangles have some common point. A point belongs to a rectangle if this point is strictly inside the rectangle or belongs to its boundary.
Find any point with integer coordinates that belongs to at least (n−1)(n−1) given rectangles.
Input
The first line contains a single integer nn (2≤n≤1326742≤n≤132674) — the number of given rectangles.
Each the next nn lines contains four integers x1x1, y1y1, x2x2 and y2y2 (−109≤x1<x2≤109−109≤x1<x2≤109, −109≤y1<y2≤109−109≤y1<y2≤109) — the coordinates of the bottom left and upper right corners of a rectangle.
Output
Print two integers xx and yy — the coordinates of any point that belongs to at least (n−1)(n−1) given rectangles.
Examples
input
Copy
3 0 0 1 1 1 1 2 2 3 0 4 1
output
Copy
1 1
input
Copy
3 0 0 1 1 0 1 1 2 1 0 2 1
output
Copy
1 1
input
Copy
4 0 0 5 5 0 0 4 4 1 1 4 4 1 1 4 4
output
Copy
1 1
input
Copy
5 0 0 10 8 1 2 6 7 2 3 5 6 3 4 4 5 8 1 9 2
output
Copy
3 4
Note
The picture below shows the rectangles in the first and second samples. The possible answers are highlighted.
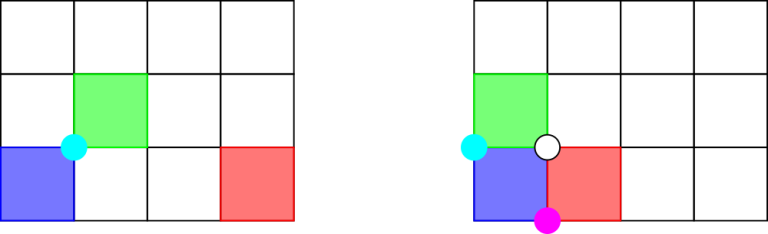
The picture below shows the rectangles in the third and fourth samples.
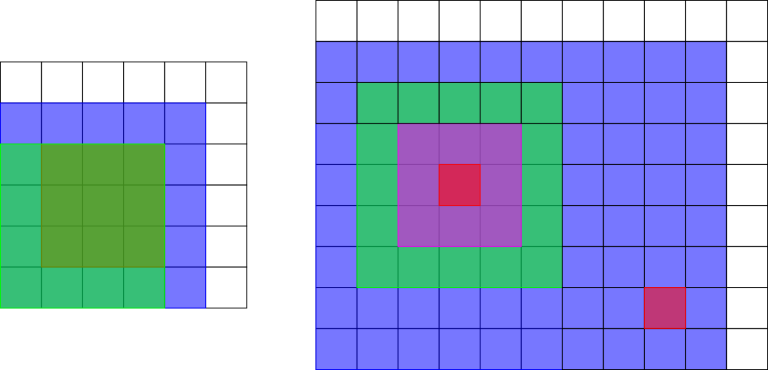
题意:
给你n个矩阵的左下角的点和右上角的点,让你求出一点使得这个点包含最少n-1个矩阵。(题目数据保证一定有解)。
题目分析:
因为题目中要求我们求出一个包含n-1个矩阵的点,因此我们不难想到这个点一定是在这n个矩形的面积并中。因此我们考虑从面积并入手解决问题。
考虑我们优先对矩形进行正向遍历,在遍历过程中不断维护前缀面积并pre,此时我们可以发现,正向遍历后的结果必为存在一个至少包含n-1个面积并矩形或者不存在矩形。而根据题意必定有解,则此时,倘若我们反向遍历,在遍历过程中维护后缀面积并suf,则此时遍历后的结果必定有一个面积并矩形。而我们的答案则必定是在正反遍历后得到的面积并矩阵之中。
因此我们只需要枚举前缀面积并pre和后缀面积并suf,并在最后判断得到的每一个面积并矩形是否能构成矩形即可。
代码:
#include <bits/stdc++.h>
#define maxn 150000
using namespace std;
const int INF=0x3f3f3f3f;
struct node{
int lx,ly,rx,ry;
node(){}
node(int _lx,int _ly,int _rx,int _ry){
lx=_lx,ly=_ly,rx=_rx,ry=_ry;
}
}q[maxn],pre[maxn],suf[maxn];
bool judge(node a){
if(a.lx>a.rx||a.ly>a.ry) return false;
return true;
}
int main()
{
int n;
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%d%d%d%d",&q[i].lx,&q[i].ly,&q[i].rx,&q[i].ry);
}
pre[0].lx=pre[0].ly=-INF;
pre[0].rx=pre[0].ry=INF;
for(int i=1;i<=n;i++){//维护前缀面积并
pre[i].lx=max(pre[i-1].lx,q[i].lx);
pre[i].ly=max(pre[i-1].ly,q[i].ly);
pre[i].rx=min(pre[i-1].rx,q[i].rx);
pre[i].ry=min(pre[i-1].ry,q[i].ry);
}
suf[n+1].lx=suf[n+1].ly=-INF;
suf[n+1].rx=suf[n+1].ry=INF;
for(int i=n;i>=1;i--){//维护后缀面积并
suf[i].lx=max(suf[i+1].lx,q[i].lx);
suf[i].ly=max(suf[i+1].ly,q[i].ly);
suf[i].rx=min(suf[i+1].rx,q[i].rx);
suf[i].ry=min(suf[i+1].ry,q[i].ry);
}
for(int i=1;i<=n;i++){
int tmplx=max(pre[i-1].lx,suf[i+1].lx);
int tmply=max(pre[i-1].ly,suf[i+1].ly);
int tmprx=min(pre[i-1].rx,suf[i+1].rx);
int tmpry=min(pre[i-1].ry,suf[i+1].ry);
if(judge(node(tmplx,tmply,tmprx,tmpry))){//判断是否能构成矩形
cout<<tmplx<<" "<<tmply<<endl;
return 0;
}
}
return 0;
}