Python3标准库：fractions有理数

1. fractions有理数

Fraction类基于numbers模块中Rational定义的API来实现有理数的数值运算。

1.1 创建Fraction实例

与decimal模块类似，可以采用多种方式创建新值。一种简便的方式是由单独的分子和分母值来创建。

import fractions

for n, d in [(1, 2), (2, 4), (3, 6)]:
    f = fractions.Fraction(n, d)
    print('{}/{} = {}'.format(n, d, f))

计算新值时要保持最小公分母。

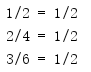
创建Fraction的另一中方法是使用<numerator> / <numerator>字符串表示。

import fractions

for s in ['1/2', '2/4', '3/6']:
    f = fractions.Fraction(s)
    print('{} = {}'.format(s, f))

解析这个字符串，以找出分子和分母值。

字符串还可以使用更常用的小数或浮点数记法，即用一个小数点分隔的一系列数字。能够由float()解析而且不表示NaN或无穷大值的所有字符串都被支持。

import fractions

for s in ['0.5', '1.5', '2.0', '5e-1']:
    f = fractions.Fraction(s)
    print('{0:>4} = {1}'.format(s, f))

浮点值表示的分子和分母值会自动计算。

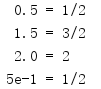
还可以从有理数的其他表示(如float或Decimal)直接创建Fraction实例。

import fractions

for v in [0.1, 0.5, 1.5, 2.0]:
    print('{} = {}'.format(v, fractions.Fraction(v)))

 不能精确表示的浮点值可能会得到意料外的结果。

使用值的Decimal表示则会给出期望的结果。

import decimal
import fractions

values = [
    decimal.Decimal('0.1'),
    decimal.Decimal('0.5'),
    decimal.Decimal('1.5'),
    decimal.Decimal('2.0'),
]

for v in values:
    print('{} = {}'.format(v, fractions.Fraction(v)))

Decimal的内部实现不存在标准浮点数表示的精度误差。

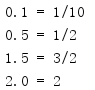
1.2 算术运算 

一旦分数被实例化，就可以在数学表达式中使用了。

import fractions

f1 = fractions.Fraction(1, 2)
f2 = fractions.Fraction(3, 4)

print('{} + {} = {}'.format(f1, f2, f1 + f2))
print('{} - {} = {}'.format(f1, f2, f1 - f2))
print('{} * {} = {}'.format(f1, f2, f1 * f2))
print('{} / {} = {}'.format(f1, f2, f1 / f2))

分数运算支持所有标准操作符。

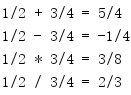
1.3 近似值

Fraction有一个有用的特性，即能够将一个浮点数转换为一个近似的有理数值。

import fractions
import math

print('PI       =', math.pi)

f_pi = fractions.Fraction(str(math.pi))
print('No limit =', f_pi)

for i in [1, 6, 11, 60, 70, 90, 100]:
    limited = f_pi.limit_denominator(i)
    print('{0:8} = {1}'.format(i, limited))

可以通过限制分母大小来控制这个分数的值。