AcWing 1307. 牡牛和牝牛

题目传送门

一、算法分析

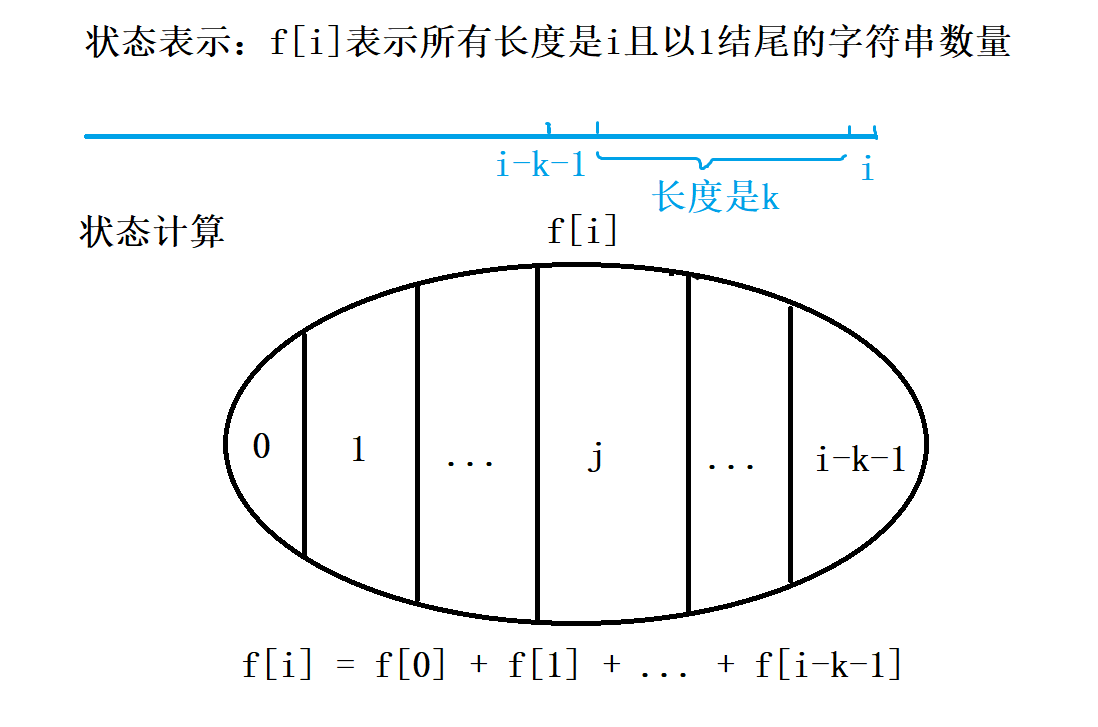
• 初始化：f[0] = 1(f[0]表示不摆放1的情况，初始值这么设，能让整个递推过程的边界是正确的则可行)
• 结果：f[0] + f[1] + f[2] + ... + f[n]

通过s[i]记录f[0] + ... + f[i]的前缀和可以优化到\(O(n)\)

二、朴素版本

#include <bits/stdc++.h>
using namespace std;

const int N = 100010, mod = 5000011;

int n, k;
int f[N];
// PASS 8/12 其它的TLE，需要优化
int main() {
    cin >> n >> k;
    f[0] = 1; //表示没有公牛
    for (int i = 1; i <= n; i++) {
        if (i - k - 1 < 0)
            f[i] = 1; //如果是前几个，不足k个的时候，其实每个位置，
        //都是可能做为公牛位的，但是，只有一种可能，就是它是公牛位，它前面都不是公牛位
        else {
            //当位置超过了 i-k-1(看图)，如果当前位是公牛位，那么前一个公牛位就需要枚举每个可能的位置了
            for (int j = 0; j <= i - k - 1; j++) f[i] = (f[i] + f[j]) % mod;
        }
    }

    int res = 0;
    for (int i = 0; i <= n; i++) res = (res + f[i]) % mod;

    printf("%d\n", res);
    return 0;
}

三、递推版本I

#include <bits/stdc++.h>
using namespace std;

const int N = 100010, mod = 5000011;

int n, k;
int f[N], s[N];

int main() {
    cin >> n >> k;

    f[0] = s[0] = 1;
    for (int i = 1; i <= n; i++) {
        if (i - k - 1 > 0)
            f[i] = s[i - k - 1]; //利用前缀和优化
        else
            f[i] = 1;

        s[i] = (s[i - 1] + f[i]) % mod; //维护前缀和
    }
    cout << s[n] << endl;
    return 0;
}

四、递推优化版本

#include <bits/stdc++.h>
using namespace std;

const int N = 100010, mod = 5000011;

int n, k;
int f[N], s[N];

int main() {
    cin >> n >> k;

    f[0] = s[0] = 1;
    for (int i = 1; i <= n; i++) {
        f[i] = s[max(i - k - 1, 0)];    //利用前缀和优化
        s[i] = (s[i - 1] + f[i]) % mod; //维护前缀和
    }
    cout << s[n] << endl;
    return 0;
}