题目传送门
https://www.luogu.com.cn/problem/CF786B
一、题目大意

二、解决思路
线段树优化建图的板子题
不难想到直接从一个点向其他点跑出最短路就完事了。但是,观察数据我们不难发现,这样边数一下就爆炸了。考虑到是区间建边,可以采用线段树优化建图的策略,优化边数。
简单地介绍一下线段树优化建图的策略:
我们以一段\(1-n\)的区段为例子:
我们建立两棵树,一棵代表入,一棵代表出:
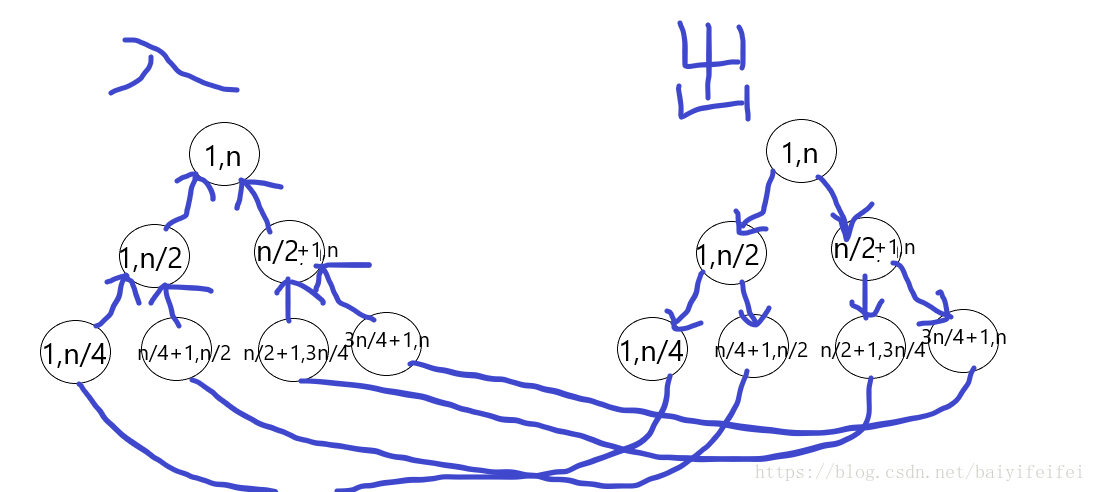
入树上所有的节点向他们的父亲节点连边,出树从父节点向子节点连边,所有的叶子节点之间连接上双向边(这些边的权值都是\(0\))。这样我们可以试着推导一下,假设从\(v\)点向\([l,r]\)之间连边,那么从\(v\)到\([l,r]\)之间的点\(u\)就会经过\(v\)点,\(u\)所在的区间的节点再到达\(u\),而如果从\([l,r]\)到\(v\)连边,那么从\([l,r]\)之间的\(u\)点就会进过\(u\)所在的区间节点到\(v\)节点,而叶子节点之间连接双向边也是保证了到达一个节点之后可以继续向其他节点走。
我们把区间映射到线段树的一个一个点上,然后建两颗线段树,第一颗线段树自上向下建边,边权为\(0\),第二颗线段树自下往上建边,边权为\(0\),这样就可以做到两颗线段树内的点互相走通,然后操作\(2\)可以在第一个线段树内加边,操作\(3\)可以在第二个线段树内加边。
三、代码实现
#include <bits/stdc++.h>
// 原理解析
// https://www.cnblogs.com/maoyiting/p/13764109.html
using namespace std;
typedef long long LL;
const LL INF = 0x3f3f3f3f3f3f3f3f;
const int N = 100100 << 3, M = N << 2;
typedef pair<LL, int> PII;
//最短路径
LL d[N]; //最短距离数组
bool st[N];
//邻接表
int e[M], h[N], idx, w[M], ne[M];
void add(int a, int b, int c) {
e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}
struct Node {
int l, r;
int ls, rs; //左儿子编号,右儿子编号
} tr[N];
int rtin, rtout, cnt; //出树根编号,入树根编号,编号计数器(从n+1开始,前面n个留给真实节点)
/**
* @brief 构建线段树
*
* @param l 左边界
* @param r 右边界
* @param flag true:点到区间 false:区间到点
* @return int 返回新创建的节点编号
*/
int build(int l, int r, bool flag) {
if (l == r) {
tr[l] = {l, r}; // tr[l]:叶子节点比较牛B,不用计数器生成节点号,而是真实的[1~n]。
return l;
}
int u = ++cnt; //非叶子节点利用cnt获取节点号
tr[u] = {l, r}; //记录区间范围
int mid = (l + r) >> 1;
tr[u].ls = build(l, mid, flag); //构建左子树
tr[u].rs = build(mid + 1, r, flag); //构建右子树
//节点到区间,区间(虚拟节点u)向左右儿子连一条权值为0的边,打通最后100米
flag ? add(u, tr[u].ls, 0) : add(tr[u].ls, u, 0);
//区间到节点,左右儿子向区间(虚拟节点u)连一条权值为0的边,打通最后100米
flag ? add(u, tr[u].rs, 0) : add(tr[u].rs, u, 0);
//返回新创建的节点编号
return u;
}
/**
* @brief 点向区间连边 或 区间向点连边
*
* @param u 线段树根节点u
* @param x 需要连边的点
* @param l 区间左边界
* @param r 区间右边界
* @param w 权值
* @param flag 哪种类型 true:点向区间 false:区间向点
*/
void add(int u, int x, int l, int r, int w, bool flag) {
if (l <= tr[u].l && tr[u].r <= r) {
flag ? add(x, u, w) : add(u, x, w);
return;
}
if (l <= tr[tr[u].ls].r) add(tr[u].ls, x, l, r, w, flag);
if (r >= tr[tr[u].rs].l) add(tr[u].rs, x, l, r, w, flag);
}
void dijkstra(int s) {
memset(d, 0x3f, sizeof(d));
d[s] = 0;
priority_queue<PII, vector<PII>, greater<PII>> q;
q.push({0, s});
while (q.size()) {
int u = q.top().second;
q.pop();
if (st[u]) continue;
st[u] = true;
for (int i = h[u]; ~i; i = ne[i]) {
int j = e[i];
if (d[j] > d[u] + w[i]) {
d[j] = d[u] + w[i];
q.push({d[j], j});
}
}
}
}
int main() {
memset(h, -1, sizeof h);
int n, q, s;
scanf("%d%d%d", &n, &q, &s);
//构建出树和入树
cnt = n; //可用的合法编号从n+1开始
rtin = build(1, n, true); //构建入树
rtout = build(1, n, false); //构建出树
int op, x, y, l, r, w;
for (int i = 1; i <= q; i++) {
scanf("%d", &op);
if (op == 1) { //点x到点y有一条边权w的边
scanf("%d%d%d", &x, &y, &w);
add(x, y, w);
} else if (op == 2) { //点x到区间[l,r]有一条边权w的边
scanf("%d%d%d%d", &x, &l, &r, &w);
add(rtin, x, l, r, w, true);
} else if (op == 3) { //区间[l,r]到点x有一条边权w的边
scanf("%d%d%d%d", &x, &l, &r, &w);
add(rtout, x, l, r, w, false);
}
}
//最短路径
dijkstra(s);
//输出最短路
for (int i = 1; i <= n; i++)
printf("%lld ", d[i] == INF ? -1 : d[i]);
putchar('\n');
return 0;
}