今天想了一下关于概率论的一维数据期望、方差以及高维数据的矩阵表示,突然想到为什么在一维中
方差的表示为:V(x) = E((x-E(x))2)
而到了高维,这样的表述就成了协方差呢?V(X) = E((X-µ)(X-µ)T), 它为什么可以表示协方差呢?于是拿出笔自己推到了一下,果然!
详细推导过程见下图:
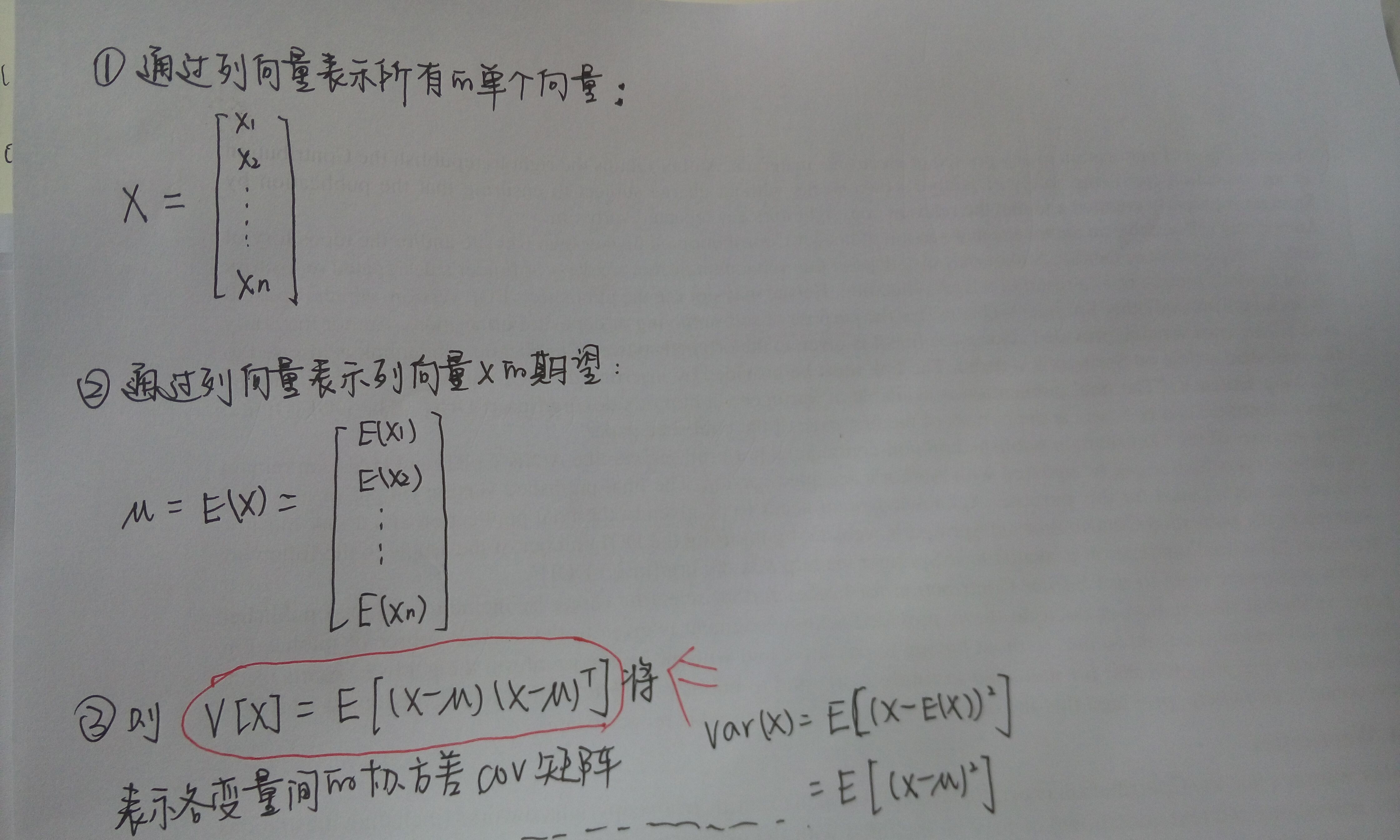

所以,我们可以得出 V(X) = E((X-µ)(X-µ)T) 其实就是描述了变量之间的协方差,就是协方差矩阵。
今天想了一下关于概率论的一维数据期望、方差以及高维数据的矩阵表示,突然想到为什么在一维中
方差的表示为:V(x) = E((x-E(x))2)
而到了高维,这样的表述就成了协方差呢?V(X) = E((X-µ)(X-µ)T), 它为什么可以表示协方差呢?于是拿出笔自己推到了一下,果然!
详细推导过程见下图:


所以,我们可以得出 V(X) = E((X-µ)(X-µ)T) 其实就是描述了变量之间的协方差,就是协方差矩阵。