[CQOI2018]解锁屏幕

Description:

使用过Android 手机的同学一定对手势解锁屏幕不陌生。Android 的解锁屏幕由3X3 个点组成，手指在屏幕上画一条线，将其中一些点连接起来，即可构成一个解锁图案。如下面三个例子所示

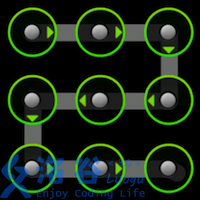
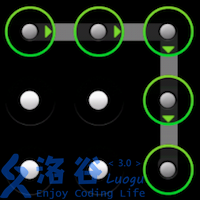
题目描述:

画线时还需要遵循一些规则:

连接的点数不能少于4 个。也就是说只连接两个点或者三个点会提示错误。

两个点之间的连线不能弯曲。

每个点只能“使用”一次，不可重复。这里的“使用”是指手指划过一个点，该点变绿。

两个点之间的连线不能“跨过”另一个点，除非那个点之前已经被“使用”过了。

对于最后一条规则，参见下图的解释。左边两幅图违反了该规则; 而右边两幅图(分别为2->4-1-3-6 和6->5-4->1->9-2) 则没有违反规则，因为在“跨过”点时，点已经被“使用”过了。

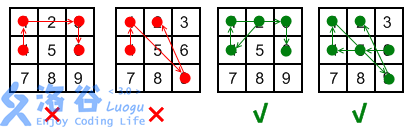
现在工程师希望改进解锁屏幕，增减点的数目，并移动点的位置，不再是一个九宫格形状，但保持上述画线的规则不变。请计算新的解锁屏幕上，一共有多少满足规则的画线方案。

Hint:

(n le 20)

Solution:

状压SB题,但是被细节坑了好多次??

#include <bits/stdc++.h>
#include <set>
#include <stack>
#include <cmath>
#include <queue>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <iostream>
#include <algorithm>
#define ls p<<1 
#define rs p<<1|1
#define blt(i) __builtin_popcount(i)
using namespace std;
typedef long long ll;
const int mod=1e8+7;
inline int read() {
    char c=getchar(); int x=0,f=1;
    while(c>'9'||c<'0') {if(c=='-') f=-1;c=getchar();}
    while(c<='9'&&c>='0') {x=(x<<3)+(x<<1)+(c&15);c=getchar();}
    return x*f;
}
inline int chkmax(int &x,int y) {if(x<y) x=y;}
inline int chkmin(int &x,int y) {if(x>y) x=y;}

const int mxn=1e6+5; //数组开小,WA成狗
int n,ans,x[mxn],y[mxn],dp[mxn][25];
int f[55][55]; //一开始用map.....结果TLE成狗23333

int check(int a,int b,int t) {
    int tp=f[a][b];
    if((tp&t)==tp) return 1;
    else return 0;
}

int main()
{
    n=read();
    for(int i=1;i<=n;++i) 
        x[i]=read(),y[i]=read();
    for(int i=1;i<=n;++i) {
        for(int j=i+1;j<=n;++j) {
            for(int k=1;k<=n;++k) {
                if(k==i||k==j) continue ;
                if((y[i]-y[k])*(x[i]-x[j])==(x[i]-x[k])*(y[i]-y[j]))
                    if((x[k]-x[j])*(x[k]-x[i])<0||(y[k]-y[i])*(y[k]-y[j])<0) //注意还要考虑线段的多种情况 
                        f[i][j]|=(1<<(k-1)),f[j][i]=f[i][j];		
            }
        }
    }	
    for(int i=0;i<n;++i) dp[(1<<i)][i+1]=1;
    for(int i=1;i<(1<<n);++i) {
        for(int j=1;j<=n;++j) {
            if(i&(1<<(j-1)))
            for(int k=0;k<n;++k) 
                if(!(i>>k&1)) 
                    if(check(j,k+1,i)) 
                        (dp[i|(1<<k)][k+1]+=dp[i][j])%=mod;
            
            if(blt(i)>3) ans=(ans+dp[i][j])%mod;
        }
    }
    printf("%d",ans);
    return 0;
}