一些概念:
-
损失函数:单个训练示例的误差。最经典的是“平方误差”来计算,即预测值与实际值差值的平方。
-
代价函数:整个训练集的损失函数的平均值。
-
最优化:求损失函数达到最小时的权重和偏置。
-
学习率:训练神经网络时,通常使用梯度下降法来优化参数。在每次迭代中,我们都使用反向传播来计算每个权重的损失函数的导数,并从这个权重中减去它。学习率决定了你想要更新权重(参数)值的速度。学习率不能太低导致收敛的速度缓慢,也不能太高导致找不到局部最小值。
-
epoch:循环训练的次数。
-
batch:批次,就是每次训练模型时,喂入的数据的大小。
对神经网络的理解:
现在有一个 目标函数f*(x)
我们只知道目标函数的 输入和输出(x和y,也就是feature和label)。
我们的目的是通过已知的输入和输出,去得到目标函数f*(x)。
我们可以定义一个f(x),然后让这个函数去近似目标函数。神经网络就是类似的例子,
它可以理解成:
-
通过搭建神经网络,构建出一个函数f(x)(函数可以有多层嵌套,相当于多层神经网络)。
-
通过f(x)对输入x的学习,会不断优化自身的参数,最终近似于f*(x)。
神经元

神经网络的每一层中,都有很多神经元,每一个神经元都可以看作是一个函数,这个函数称为激活函数。
第一层神经元没有输入、最后一层神经元没有输出。除此以外,每个神经元都含有:
-
输入x
-
权重(weight), 记作:w。
-
偏置(bias),记作:b。
-
激活函数f(x)
-
输出y
除第一层神经元之外,其余神经元的输入( x(i+1) )皆为上一层神经元的输出( y(i) )。
xi+1 = yi = f(x * w) = f(x1 * w1 + x2 * w2 + ... + xn * wn)
(n为神经元个数)

这时候,如果我们对神经元是否激活有其他的要求。
-
如即使加权和大于0,你也不想激活这个神经元;
-
或者是当加权和大于10时,才激活神经元。
所以引入了 偏置值 的概念,它起到一个阈值的作用。
在 t 时刻神经元得到输入X(t),只有当X(t) 大于偏置值b的时候,神经元才会在 t + 1 时刻被激活(激活的意思是有输出),否则不会被激活。
如:我们需要当加权和大于10时,才激活神经元。此时偏置值就是:-10。
所以,上述公式变成:
x(i+1) = y(i) = f(x * w - b) = f[(x1 * w1 - b1) + (xn * wn - bn) + ... + (xn * wn - bn)]
这时候,我们可以把多加一个输入X0,并把它的值设为 - 1。还可以把偏置b当成权重w0。
所以最终公式为:
yi = f(x * w) = f(x0 * w0 + x1 * w1 + ... + xn * wn)
(x0 为 -1,w0 为 偏置b的值。)
激活函数f(x):
如果我们对输出有要求,需要对输出的值进行某种限制,这时就需要用到激活函数。激活函数的作用是能够给神经网络加入一些非线性因素,使得神经网络可以更好地解决较为复杂的问题。
-
Sigmoid(): 可以将输出的值映射到[0, 1]的区间又称
Logistic曲线
-
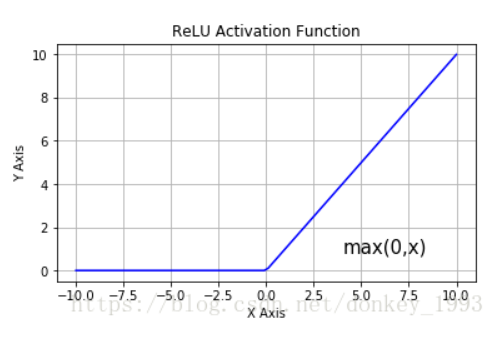
Relu():
训练:
每一层都带有权重和偏置,一个网络中的偏置和权值非常多。相当于这个网络有无数个旋钮开关让我们调整,得到我们想要的那个结果。所以,当我们讨论神经网络如何“学习”(又称“训练”)的时候,实际上说的是:我们应该怎样去设置这么多的参数
=================================================
f3( f2( f1(x) ) )
-
每一个函数为一层网络
-
f1(x) 为第一层,也称作 输入层
-
f3(x) 为最后一层,也称作 输出层
神经网络的核心是:
一层的激活值,通过某种运算,算出下一层的激活值。
机器学习:利用经验改善性能。
神经网络:利用网络自学习算法来确定参数。
神经网络如何得到参数:
- 强化合意的行为。
- 弱化不合意的行为。