Filling the Grid
Introduce
Suppose there is a (h×w) grid consisting of empty or full cells. Let's make some definitions:
- (r_i) is the number of consecutive full cells connected to the left side in the (i)-th row ((1≤i≤h)). In particular, (r_i=0) if the leftmost cell of the (i)-th row is empty.
- (c_j) is the number of consecutive full cells connected to the top end in the (j)-th column ((1≤j≤w)). In particular, (c_j=0) if the topmost cell of the (j)-th column is empty.
In other words, the (i)-th row starts exactly with (r_i) full cells. Similarly, the (j)-th column starts exactly with (c_j) full cells.
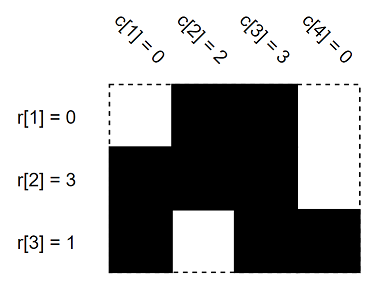
These are the (r) and (c) values of some (3×4) grid. Black cells are full and white cells are empty.
You have values of (r) and (c). Initially, all cells are empty. Find the number of ways to fill grid cells to satisfy values of (r) and (c). Since the answer can be very large, find the answer modulo (1000000007(10^9+7)). In other words, find the remainder after division of the answer by (1000000007(10^9+7)).
Input
The first line contains two integers (h) and (w) ((1≤h,w≤10^3)) — the height and width of the grid.
The second line contains (h) integers (r_1,r_2,…,r_h (0≤r_i≤w)) — the values of (r).
The third line contains (w) integers (c1,c2,…,cw (0≤c_j≤h)) — the values of (c).
Output
Print the answer modulo (1000000007(10^9+7)).
Examples
input
3 4 0 3 1 0 2 3 0
output
2
input
1 1 0 1
output
0
input
19 16 16 16 16 16 15 15 0 5 0 4 9 9 1 4 4 0 8 16 12 6 12 19 15 8 6 19 19 14 6 9 16 10 11 15 4
output
797922655
Note
In the first example, this is the other possible case.
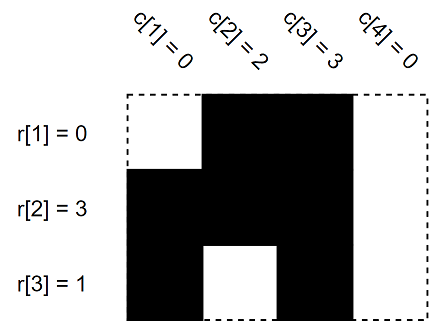
In the second example, it's impossible to make a grid to satisfy such (r), (c) values.
In the third example, make sure to print answer modulo ((10^9+7)).
题解
题目要求在网格满足一定条件下有多少种可能。
因为输入(r_j)时,第(j)行的前(r_j+1)个网格是确定的(前(r_j)个是黑色,第(r_j+1)个是白色)。
那么我们只要枚举每个位置是否同时在(r_j+1)和(c_i+1)之外。
找出这些位置的个数,因为这些位置可以为白或黑。
满足条件的方案数就是(pow(2,sum))。
时间复杂度是(O(hw))的。
这里要注意一下:
当行和列的一些条件相悖的时候,方案数应为0。
例如在((j,r_j+1))的位置上满足(r)的要求是白色的,但是如果(j≤c{r_j+1}),也就是满足(c)的要求是黑色,那么方案数就为0。
上代码:
#include<bits/stdc++.h>
#define mod 1000000007
using namespace std;
int n,m,ans;
int a[1009],b[1009];
long long ksm(int p){
long long s=2;
long long ans=1;
while(p){
if(p&1) ans*=s;
ans%=mod;
s=s*s%mod;
p/=2;
}
return ans;
}
int main(){
scanf("%d%d",&n,&m);
for(int j=1;j<=n;j++)
scanf("%d",&a[j]);
for(int j=1;j<=m;j++)
scanf("%d",&b[j]);
for(int j=1;j<=n;j++)
if(j<=b[a[j]+1]){
printf("0");
return 0;
}
for(int j=1;j<=m;j++)
if(j<=a[b[j]+1]){
printf("0");
return 0;
}
for(int j=1;j<=n;j++)
for(int i=a[j]+2;i<=m;i++)
if(j>b[i]+1) ans++;
printf("%lld",ksm(ans));
return 0;
}