FFT理解

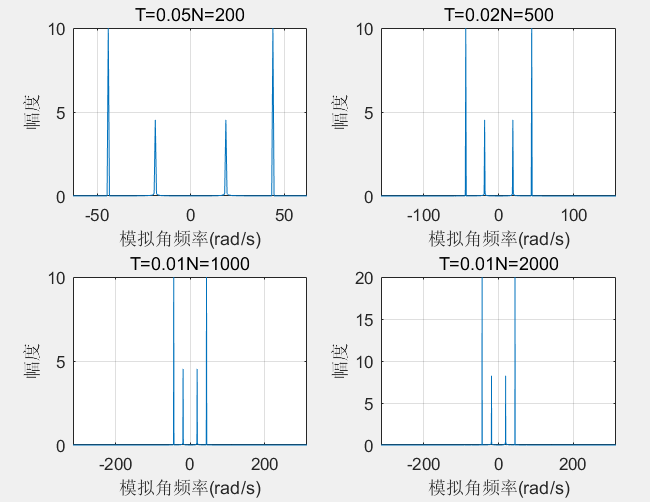
 *连续时间-周期性信号频谱

clc;clear;close all
N = input('N= ');
T = 0.05;
n = 1:N;
%原始数据输入
D = 2*pi/(N*T);
%计算分辨率
xa=cos(10*n*T);
%有限长余弦序列
Xa=T*fftshift(fft(xa,N));  %Xa(1)
%求x(n)的DFT，移动到对称位置
k=floor(-(N-1)/2:(N-1)/2);
%对于w=0对称的奈奎斯特频率下标向量
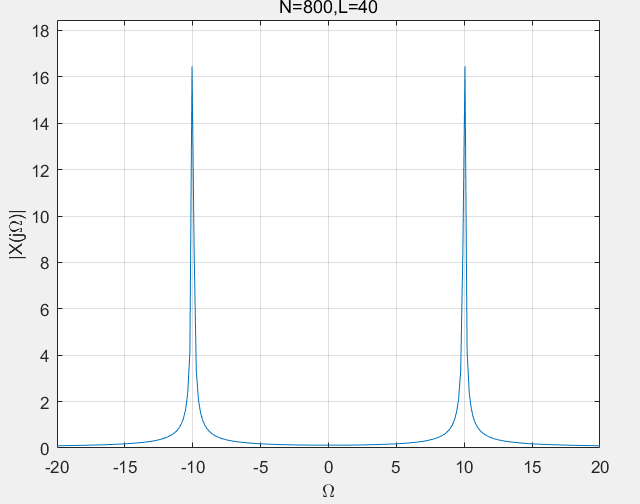
TITLE=sprintf('N=%i,L=%i',N,N*T);
%变数值为格式控制下的字符串
plot(k*D,abs(Xa));
axis([-20,20,0,max(abs(Xa))+2]);
xlabel('Omega');ylabel('|X(jOmega)|')
title(TITLE);
grid;

 

关于 fftshift函数：用于将数组进行循环移位，以达到对fft结果的负分量进行移位，方便结果的绘制；

https://ww2.mathworks.cn/help/matlab/ref/fftshift.html

*连续时间-非周期信号的频谱

综上： 抽样间隔T要选择足够小，以避免频谱的混叠失真，而截断长度L=NT要选择足够大，以减少截断效应，提高频率分辨率。建议采用以下步骤：

     1：先选定L不变，T逐步减少，直到频谱混叠的影响逐步减少到可以容忍的程度（研究-π/T或π/T处的频谱值），得到此时的T值；

     2：增加L值（实质上就是增加有效数据长度），使得截断效应减少，这时采用上面已求的最小T值。直到频谱的差别很小时，得到此时的L值。

 所以只需赋L/T两个变量值，N=L/T就能随之改变，总之要赋值N/L/T中两个变量即可。

编程下例：

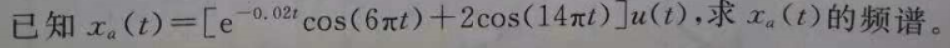
clear;clc
T0=[0.05,0.02,0.01,0.01];                                   %四种抽样间隔
L0=[10,10,10,20];                                           %四种信号记录长度，N=L0(i)/T0(i)
for i=1:4
	T=T0(i); N=L0(i)/T0(i);                             %按顺序选用T和L
	D=2*pi/(N*T);                                       %频率分辨率
	n=0:N-1;
	x=exp(-0.02*n*T).*cos(6*pi*n*T)+2*cos(14*pi*n*T);   %序列
	k=floor(-(N-1)/2 : (N-1)/2);
	X=T*fftshift(fft(x));
	[i,X(i)]                                            %检测四次循环在奈奎斯特频率处的幅度
	subplot(2,2,i),plot(k*D,abs(X));
	xlabel('模拟角频率(rad/s)');ylabel('幅度');grid
	axis([min(k*D),max(k*D),0,inf]);                    %坐标范围
	str=['T=',num2str(T),'N=',num2str(N)];title(str);   %标题显示抽样间隔和FFT点数N  
end