之前刷leetcode的时候,知道求排列组合都需要深度优先搜索(DFS), 那么前序、中序、后序遍历是什么鬼,一直傻傻的分不清楚。直到后来才知道,原来它们只是DFS的三种不同策略。
N = Node(节点)
L = Left(左节点)
R = Right(右节点)
在深度优先搜索的时候,以Node的访问顺序,定义了三种不同的搜索策略:
前序遍历:结点 —> 左子树 —> 右子树
中序遍历:左子树—> 结点 —> 右子树
后序遍历:左子树 —> 右子树 —> 结点
##前序遍历
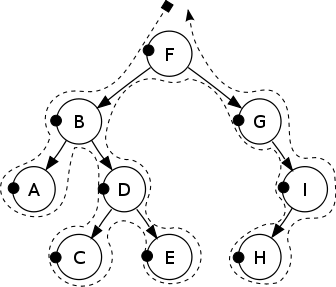
Pre-order: F, B, A, D, C, E, G, I, H.
##中序遍历
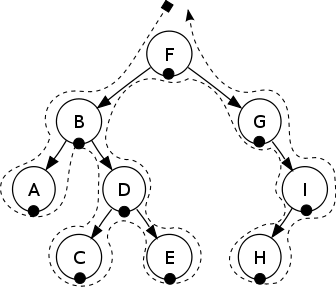
In-order: A, B, C, D, E, F, G, H, I.
在二叉搜索树(BST)中,中序遍历返回递增的一个序列
##后序遍历
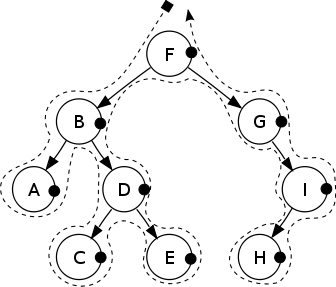
Post-order: A, C, E, D, B, H, I, G, F.
##递归代码
递归实现比较直观容易,通常DFS遍历,都需要传递一个参数 or 设置一个全局变量,来保存结果
def pre_order(self, node, results):
if node is None:
return
results.append(node.val)
self.pre_order(node.left, results)
self.pre_order(node.right, results)
def in_order(self, node, results):
if node is None:
return
self.in_order(node.left, results)
results.append(node.val)
self.in_order(node.right, results)
def post_order(self, node, results):
if node is None:
return
self.post_order(node.left, results)
self.post_order(node.right, results)
results.append(node. 大专栏 树的三种DFS策略(前序、中序、后序)遍历val)
##非递归代码
深度优先遍历的非递归代码,一定用到的是stack数据接口
非递归实现前序和中序还可以,后续遍历就非常烧脑了
前序最简单,相当于for循环所有children,所以一版非递归DFS,就用前序就好了。
中序遍历,由于对于BST有一个递增的特性,所以还是比较常用的
def preorderTraversal(self, root):
results = []
if root is None:
return results
stack = [root]
while(len(stack) > 0):
node = stack.pop()
results.append(node.val)
# right first so left pop fisrt
if node.right is not None:
stack.append(node.right)
if node.left is not None:
stack.append(node.left)
return results
def inorderTraversal(self, root):
results = []
if root is None:
return results
stack = []
node = root
while(len(stack) > 0 or node is not None):
if (node is not None):
stack.append(node)
node = node.left
else:
node = stack.pop()
results.append(node.val)
node = node.right
return results
def postorderTraversal(self, root):
results = []
if root is None:
return results
node = root
stack = []
lastNodeVisted = None
while(len(stack) > 0 or node is not None):
if node is not None:
stack.append(node)
node = node.left
else:
peek = stack[-1] # last element
if (peek.right is not None and lastNodeVisted != peek.right):
node = peek.right
else:
results.append(peek.val)
lastNodeVisted = stack.pop()
return results
–END–