NB模型概率估计很差，但分类效果很好。
朴素贝叶斯是产生模型，所以是要求联合概率的。
建立 NB分类器有两种不同的方法：一种多项式NB模型，它在文档的每个位置上生成词表中的一个词项。（推荐使用）
另外一种方法是多元贝努利模型（multivariate Bernoulli model）或者直接称为贝努利模型 。（该模型常出错，不推荐使用）
小规律小结
小结1：贝叶斯模型里，只要是求条件概率：p(x|y) ，即是已知隐变量类别y条件下 求可见变量x的概率 一般是可直接一步得出， 从训练集求得的，用词频相除即可求。
小结2：多项式模型 P(d|c) = P(<t1, …, tk , … , tnd >|c)，
贝努利模型 P(d|c) = P(<e1, … , ei , … , eM>|c)。
其中，< t1,… , tnd >是在d中出现的词项序列（当然要去掉那些从词汇表中去掉的词，如停用词）
<e1,… , ei , … , eM>是一个M维的布尔向量，表示每个词项在文档d中存在与否。
一、 多项式NB（multinomial NB）模型
给出文档d，求类别c：
（贝叶斯总式）
实际是求出分子即可，分母对y=1和y=0都一样。（如果是比较哪个概率大，是属于垃圾邮件概率大还是非垃圾的概率大，则分母不用求，只需比较分子即可，但下面演示例子里还是回求出分母，这样可以精确求出概率值）
对上面贝叶斯总式：1 ≤ k<nd计算其对应的条件概率的乘积，这可能会导致浮点数下界溢出。
因此，更好的方法是引入对数，从而将原公式 的计算转变成多个概率的对数之和。由于log(xy) = log(x) + log(y)，且log是单调递增函数，因 此具有较高概率对数值的类别就是最有可能的类别。因此，大多数 NB 在实现时所求的最大值 实际是
该公式选择最可能的类别作为最终的类别。
最终贝叶斯问题转换成参数估计问题：
如何估计参数p（c） 及 p(tk|c) ？
有：
其中，Nc是训练集合中c类所包含的文档数目，而N是训练集合中的文档总数。
（意思 为 t在c类文档中出现的相对频率：）
Tct是 单词t在训练集合 c类文档中出现的次数 （即在文档的词频）。B = |V| 是词汇表中所有词项的数目。分母第一项是指类别c文档的总长度（以单词为单位）
详情review《信息检索导论》对应章节！！！！
二、 贝努利模型
对于词汇表中的每个词项都对应一个二值变量，1和 0分别表示词项在文档中出现和不出现。
实例：垃圾邮件
我们最终要求的是给出某些样本x，求这些样本的类型y：（如，给出样本为邮件的所有包含单词X,求出这邮件是否为垃圾邮件y的概率）
这里假设y只有0或者1取值，1表示垃圾邮件，0非垃圾邮件。则我们最终要求的是：
对于上式，分子，i表示样本（邮件）里第i个单词，n表示一共n个单词。
因为分母一样，所以只需求分子：
（简化后，贝叶斯总共需求的公式）
这里涉及了2个概率，其实是可以一步直接求的，必须要再转换公式了！：
设p(xi = 1| y =1) = ∅i|y=1 （xi这里取值只有1或者0，表示出现或没出现，这个概率表示类别为1的垃圾邮件会出现单词xi的概率）
p(y=1) =∅y (表示在所有邮件里，垃圾邮件的概率是多少，其实就是垃圾邮件数目/总邮件数目)
把上面等式左右调换，变如下：
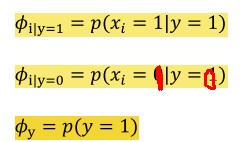（ 其中第二条公式表示y=0即非垃圾邮件出现单词Xi的概率）
所以将上面三种情况的概率都转换成了统一∅参数表示。
所以我们上面简化后的总式只需要求
三个参数最大值，即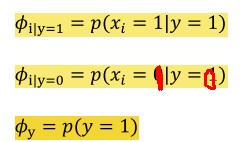三个概率最大值。
即：
=
（关键公式L）
= 或
（这步是这样吗？？）
所以三个参数（三个概率值）可以用下面等式直接算出：
=
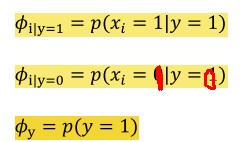这里m表示样本有m个，即有m封邮件，i表示第i封邮件。
规律小结：贝叶斯模型里，只要是求条件概率：p(x|y) ，即是已知隐变量类别y条件下求可见变量x的概率 一般是可以直接从训练集求得的，用词频相除即可求。
进而对上面三个式子继续拉普平滑，分子分母加常数：
即：
分子+1（防止新出现的词在训练集没出现过） ， 分母+k （这里z即是上面所有公式的y;ｋ是指类别y的取值范围{1,2,...k}
特别地，对垃圾邮件而言：k=2，因为y只有0或者1 取值，所以
上面三个参数改成：
=
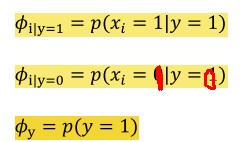以上是：文本分类的朴素贝叶斯模型， 为多值伯努利事件模型 。在这个模型中，我们首先随机选定了邮件的类（垃圾或者普通邮件，也就是 p(y)）
然后一个人翻阅词典，从第一个词到最后一个词，随机决定一个词是否要在邮件中出现，出现标示为1，否则标示为0。然后将出现的词组成 一封邮件。决定一个词是否出现依照概率 p(xi|y)。那么这封邮件的概率可以标示为 =
= 或
===========================================================================
下面以另外一种思路求文本分类，还是以邮件为例：
这次不先从词典入手，而是选择从邮件入手。
让j表示邮件中的第j个词，xj表示这个词在字典中的位置，那么xj取值范围为{1,2,…|V|}，|V|是字典中词 的数目。这样一封邮件可以表示成（X1，X2，X3,....,Xn）,n可以变化，因为每封信的个数不同。
然后我们对于每个xi随机从|V|个值中取一个，这样就形成了一封邮件。这相当 于重复投掷|V|面的骰子，将观察值记录下来就形成了一封邮件。
当然每个面的概率服从p(xj|y)，而且每次试验条件独立。这样我们得到的邮件概率是 。
居然跟上面的多值伯努利模型一样，那么不同点在哪呢？
注意第一个多值伯努利模型的n是字典中的全部的词，下面这个n是邮件中的词个数。
上面多值伯努利模型xj表示一个词是否出现，只有0和1两个值，两者概率和为1。下面的 xi=xj表示|V|中的一个值，|V|个p(xi|y)相加和为1。是多值二项分布模型。
上面多值伯努利模型的x向量都是 0/1值，下面的x的向量都是字典中的位置。
-----------------------------
总之，变量表示：V是字典词数，n是邮件词数，m表示m个样本（邮件），i表示第i个样本。X(i)表示一封邮件，Xj是指向词典的索引。如果词典有5000个词，则j范围是0到5000
，这里x^(i)表示第i封邮件（样本），其中共有ni个词，如果一封邮件有300个词，那邮件里有300个Xj^(i)个单词，
每个词在字典中的编号为
。 如果词典有5000个词，则xj范围是0到5000，
则最大似然估计公式依然同上(L式)，复制过来即可：
=
（细化成两个 连乘 号）
三个概率是：
拉普平滑后：
表示每个k值至少发生过一次。
与多值伯努利模型的式子相比，分母多了个ni，分子Xj由原来0/（1表示有没有出现在邮件里 ），变成了k（表示单词k） 。
例如:对第一个公式 phi(k|y=1)解释为:
分子是，对训练集合中所有垃圾邮件中词k出现的次数
分母是 对所有训练集合进行求和，如果其中一个样本是垃圾邮件，则将它的长度加起来
所以分母意思是，训练集合中所有垃圾邮件的总长(即垃圾邮件的总件数（即邮件为单位，非以单词为单词）)
所以这个比值的含义是 在所有垃圾邮件中 词k 所占的比例。
而在上面多值伯努利模型，这个公式意思是在垃圾邮件出现这个单词的概率。
例子：
a b c
图的列分别是a,b,c词。 行是邮件，一共4行，所以一共4封邮件。（矩阵里的权值是什么意思？？）
假如邮件中只有a，b，c这三词，他们在词典的位置分别是1,2,3，前两封邮件都只有2 个词，后两封有3个词。 Y=1是垃圾邮件。 那么，
（有错吧？？？）
解释上面答案：phi(k=1,2,3|y=1)的分母都是2+3，因为V=3，表示只有3个词。垃圾邮件一共2封（不是计算垃圾邮件单词数吗），所以为2.所以是2+3。分子是什么意思？
假如新来一封邮件为b，c那么特征表示为{2,3}。
所以非垃圾邮件概率为0.4，所以这封新邮件自然被确定为垃圾邮件了
注意这个公式与朴素贝叶斯的不同在于这里针对整体样本求的 phi(k|y=1)，
而朴素贝叶斯里面针对每个特征求的phi(xj=1|y=1)，而且这里的特征值维度是参差不齐的。
三、贝叶斯模型和LDA主题模型 比较
LDA主体模型是基于贝叶斯模型的，主要求的是：（见 LDA naive .pdf）
1.文档m属于哪个topic的概率？（符合Dir分布）
2.每个topic 产生档次Wj的概率 ？ （符合Dir分布）
举例：
文档1的第一个word，即bank这个词来评价 P(z=topic|w=bank,doc=1) ，
即求 P(z=topic|w=bank）
=p(w|z)p(z=topic) / p(w=bank)
因为分母p(w=bank)对任何topic 该值都是一样的： 即如此式
的分母一样，是对分子逐个y遍历相加 ；故可忽略
故只需求p(w|z)p(z=topic)值了。
其中p(z=topic) 即先验概率，若是贝叶斯理论，则可以一步得出结果：即此式，即用z=topic的文档数/所有topic文档数
但贝叶斯模型是监督学习的，它是有训练集的，所以上面公式可以直接根据训练集求出值，但是LDA模型 是聚类，是非监督，没有训练集，所以无法用上面式子，
且p(z =topic )是符合Dir分布， 所以：
而求p(w|z)p(z=topic) 也并非用贝叶斯公式直接可求：
而是根据Dir分布:
四、代码
最后附两个NB方法伪代码：
五、两个模型例子比较：
多项式解法：
伯努利模型解法： 
伯努利模型里的p(chinese|c)分子是3+1，3是因为有三个文档出现了chinese单词。
总之，这个模型比较