异或(^)、异或和 的性质及应用总结
异或的含义
异或运算与一般的逻辑或不同,异或算符的值为真仅当两个运算元中恰有一个的值为真,而另外一个的值为非真。转化为命题,就是:“两者的值不同。”或“有且仅有一个为真。”符号为 XOR 或 EOR 或 ⊕(编程语言中常用^)。
或在数学中的含义:一个元素在集合A中或在集合B中,或的维恩图如下:
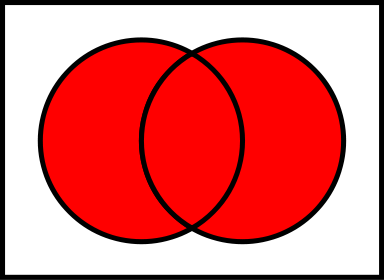
而异或是不允许共存的,所以 A ^ B 的维恩图如下:
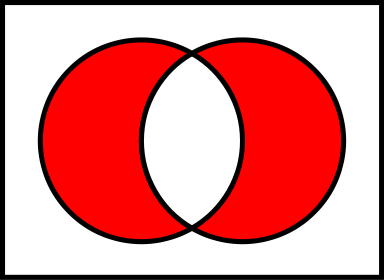
同理对于 A ^ B ^ C 维恩图:
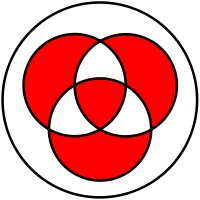
异或运算{displaystyle Aoplus B}
| A | B | ⊕ |
|---|---|---|
| F | F | F |
| F | T | T |
| T | F | T |
| T | T | F |
| A | B | ⊕ |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
任何数异或自己=把自己置0
异或的性质:满足交换律和结合律
- 交换律:A ^ B = B ^ A;
- 结合律:A ^ (B ^ C) = (A ^ B) ^ C;
- 恒等律:X ^ 0 = X;
- 归零律:X ^ X = 0;
- 自反:A ^ B ^ B = A ^ 0 = A;
- 对于任意的 X: X ^ (-1) = ~X;
- 如果 A ^ B = C 成立,那么 A ^ B = C,B ^ C = A;
异或的应用
1-1000放在含有1001个元素的数组中,只有唯一的一个元素重复,找出这个重复的数字。要求不能使用辅助存储空间并且数组的每个元素只能访问一次。
解法一:将这1001个元素加起来的和减去1+2+……+1000,所得的值就是重复的数字(数据过大容易溢出)。
解法二:异或
将1001个数全部异或得到的值再与12……^1000的结果再次异或,这样就避免了数据过大溢出的情况。
首先,异或运算满足交换律和结合律,即a^b = ba,(ab)^c = a(bc)。令重复的数字为n:
所以1 ^ 2 ^ … ^ n ^ n ^ … ^ 1000 = 1 ^ 2 ^ … ^ 1000 ^ (n ^ n) = 1 ^ 2 ^ … ^ 1000 ^ 0 = 1 ^ 2 ^ … ^ 1000(即序列中除了重复数字 n 以外所有数的异或。
如果令1 ^ 2 ^ … ^ 1000(序列中不包含n)的结果为T,那么1 ^ 2 ^ … ^ 1000(序列中包含n)的结果就是 T^n,T ^ (T ^ n) = n。
变形:一个数组存放若干整数,一个数出现奇数次,其余数均出现偶数次,找出这个出现奇数次的数。
解法与上面的解法二相同。
快速比较两个数值是否相等
a == b a^b == 0
不用额外内存,交换两个数的值
a ^= b;
b ^= a;
a ^= b;
检验和恢复,RAID5
校验和恢复主要利用的了异或的特性:IF a ^ b = c THEN a ^ c = b 应用:一个很好的应用实例是RAID5,使用3块磁盘(A、B、C)组成RAID5阵列,当用户写数据时,将数据分成两部分,分别写到磁盘A和磁盘B,A ^ B的结果写到磁盘C;当读取A的数据时,通过B ^ C可以对A的数据做校验,当A盘出错时,通过B ^ C也可以恢复A盘的数据。
使用异或使某些特定位翻转
翻转10100001的第6位, 答案:可以将该数与00100000进行按位异或运算; 10100001 ^ 00100000 = 10000001
一个整型数组里除了N个数字之外,其他的数字都出现了两次,找出这N个数字
比如,从{1, 2, 3, 4, 5, 3, 2, 4, 5}中找出单个的数字: 1
1^2^3^4^5^3^2^4^5 = 1
根据以上异或运算的特征,可以有以下用途,除方便直观外,运算性能也更加优异。
变量重置0
假设有一个变量15,二进制表示为0000 1111
0000 1111 ^ 0000 1111 = 0000 0000
a = 0000 1111
a = a ^ a
结论:同变量本身异或运算,可以将变量重置0。
指定位置取反
假设有一个变量15,二进制表示为0000 1111,将第3,4,8位取反。
0000 1111 ^ 1000 1100 = 1000 0011
结论:同指定取反位为1,其他位为0的变量进行异或运算,可以将指定位置取反。
取反后的结果,同原指定取反变量异或,可以还原变量:
1000 0011 ^ 1000 1100 = 0000 1111(15)
加密解密
假设有一个变量15,二进制表示为0000 1111,密码子为0101 0101。
加密:0000 1111 ^ 0101 0101 = 0101 1010
加密后结果是90。
将加密后结果同密码子异或,可以进行解密
0101 1010 ^ 0101 0101 = 0000 1111
解密后结果是15。
二值交换
假设两个变量:a = 15(0000 1111), b= 23(0001 0111),将两个变量交换。
1、a = a ^ b = 0000 1111 ^ 0001 0111 = 0001 1000
2、b = b ^ a = 0001 0111 ^ 0001 1000 = 0000 1111(15)
3、a = a ^ b = 0001 1000 ^ 0000 1111 = 0001 0111(23)
结论:二值交换实际上是利用了加密解密的特性。
1、a和b异或,可以把结果x看作是a、b互为密码子进行加密。
2、将x,同b(原值)异或,也就是把b作为密码子,因此可以还原a,赋值给b。
3、将x,同b(此时为a)异或,也就是把b(此时为a)作为密码子,因此还原出的值为原b,赋值给a。交换结束。
判断两值是否相等
利用同变量本身异或运算,可以将变量重置0的特性。
假设:a = 0000 1111,b = 0000 1111,则 a ^ b == 0
假设:a = 0000 1111,b = 0000 0001,则 a ^ b != 0
结论:当两个变量相等时,异或结果为0。
按位 与运算符(&)
参加运算的两个数据,按二进制位进行“与”运算。
运算规则:0&0=0; 0&1=0; 1&0=0; 1&1=1;
即:两位同时为“1”,结果才为“1”,否则为0
例如:3&5 即 0000 0011& 0000 0101 = 00000001 因此,3&5的值得1。
另,负数按补码形式参加按位与运算。
“与运算”的特殊用途:
(1)清零。如果想将一个单元清零,即使其全部二进制位为0,只要与一个各位都为零的数值相与,结果为零。
(2)取一个数中指定位
方法:找一个数,对应X要取的位,该数的对应位为1,其余位为零,此数与X进行“与运算”可以得到X中的指定位。
例:设X=10101110,
取X的低4位,用 X & 0000 1111 = 00001110 即可得到;
还可用来取X的2、4、6位。
按位 或运算符(|)
参加运算的两个对象,按二进制位进行“或”运算。
运算规则:0|0=0; 0|1=1; 1|0=1; 1|1=1;
即 :参加运算的两个对象只要有一个为1,其值为1。
例如:3|5 即 00000011 | 0000 0101 = 00000111 因此,3|5的值得7。
另,负数按补码形式参加按位或运算。
“或运算”特殊作用:
(1)常用来对一个数据的某些位置1。
方法:找到一个数,对应X要置1的位,该数的对应位为1,其余位为零。此数与X相或可使X中的某些位置1。
例:将X=10100000的低4位置1 ,用X | 0000 1111 = 1010 1111即可得到。
取 反运算符(~)
参加运算的一个数据,按二进制位进行“取反”运算。
运算规则:~1=0; ~0=1;
即:对一个二进制数按位取反,即将0变1,1变0。
使一个数的最低位为零,可以表示为:a&~1。
1的值为1111111111111110,再按“与”运算,最低位一定为0。因为“”运算符的优先级比算术运算符、关系运算符、逻辑运算符和其他运算符都高。
左移运算符(<<)
将一个运算对象的各二进制位全部左移若干位(左边的二进制位丢弃,右边补0)。
例:a = a<< 2将a的二进制位左移2位,右补0,
左移1位后a = a *2;
若左移时舍弃的高位不包含1,则每左移一位,相当于该数乘以2。
右移运算符(>>)
将一个数的各二进制位全部右移若干位,正数左补0,负数左补1,右边丢弃。
操作数每右移一位,相当于该数除以2。
例如:a = a>> 2 将a的二进制位右移2位,
左补0 or 补1得看被移数是正还是负。
运算符把expression1 的所有位向右移 expression2指定的位数。expression1的符号位被用来填充右移后左边空出来的位。向右移出的位被丢弃。
例如,下面的代码被求值后,temp 的值是 -4:
-14 (即二进制的 11110010)右移两位等于 -4(即二进制的 11111100)。
var temp = -14 >> 2
无符号右移运算符(>>>)
运算符把 expression1 的各个位向右移expression2 指定的位数。右移后左边空出的位用零来填充。移出右边的位被丢弃。
例如:var temp = -14 >>>2
变量 temp的值为 -14 (即二进制的 11111111 11111111 1111111111110010),向右移两位后等于 1073741820 (即二进制的 00111111 11111111 1111111111111100)。
复合赋值运算符
位运算符与赋值运算符结合,组成新的复合赋值运算符,它们是:
&= 例:a &=b 相当于a=a& b
|= 例:a |=b 相当于a=a |b
= 例:a >>=b 相当于a=a>> b
<<= 例:a<<=b 相当于a=a<< b
^= 例:a ^= b 相当于a=a^ b
运算规则:和前面讲的复合赋值运算符的运算规则相似。
不同长度的数据进行位运算
如果两个不同长度的数据进行位运算时,系统会将二者按右端对齐,然后进行位运算。
以“与”运算为例说明如下:我们知道在C语言中long型占4个字节,int型占2个字节,如果一个long型数据与一个int型数据进行“与”运算,右端对齐后,左边不足的位依下面三种情况补足,
(1)如果整型数据为正数,左边补16个0。
(2)如果整型数据为负数,左边补16个1。
(3)如果整形数据为无符号数,左边也补16个0。
如:long a=123;int b=1;计算a& b。
如:long a=123;int b=-1;计算a& b。
如:long a=123;unsigned intb=1;计算a & b。