上一节我们学习了堆和堆排序的一些理论知识(点击查看),今天我们就来讲一讲,堆这种数据结构的几个非常重要的应用。
应用一:优先级队列
优先队队列,是一个按优先级进出的特殊队列,一般的队列是先进先出,而优先级队列是优先级高的先出。
优先级队列与堆非常相似,一个堆可以看作一个优先级队列。往优先队队列插入一个元素,相当于往堆中插入一个元素;从优先级队列中取出优先级最高的元素,就相当于取出堆顶元素。
例子1:合并有序小文件
合并多个有序的小文件到大文件。假设有100个文件,要合并到1个文件里,要求有序。
定义一个大小为100的小顶堆,从100个文件里取出第一行,初始化小顶堆。然后取出堆顶放进大文件里,并从此数据所在的文件里再取出一行放到堆里(重新堆化),重复这个动作,直到所有文件的内容都为空。
例子2:高性能定时器
定时器维护多个定时任务,每个任务都设置了触发执行的时间点。
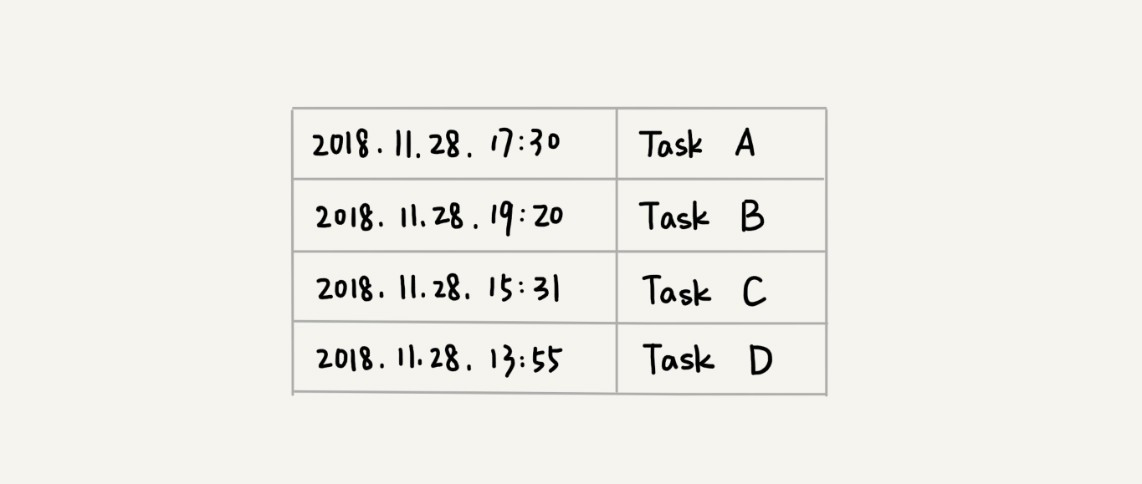
计算每个任务的时间差,弄成小顶堆。取堆顶元素的时间差,让程序睡眠,睡眠时间为此时间差,程序唤醒后,取出堆顶任务(删除堆顶元素)并执行。如果任务是重复的,再重新计算任务的时间差,并插入堆里。
应用二:利用堆求Top K
抽象成两类问题:静态数据集合和动态数据集合
实现方式:定义一个大小为K的小顶堆,顺序遍历数组,逐一与堆顶进行比较,假设比它大,则删除堆顶再插入后堆化。假设小于等于它,则忽略。
对于动态数组,可维护一个实时的堆,当有数据插入数组,与堆顶判断,比它大则插入堆,否则忽略。并且插入到数组中。
时间复杂度:O(nlogk)。遍历数组O(n),每次替换(堆化)O(logk)。
应用三:利用堆求中位数
中位数指在有序数据中处于中间位置的那个数据。如果数据个数为奇数,则中位数是n/2+1位置的数,如果是偶数,则是n/2和n/2+1,可取其中的任意一个。
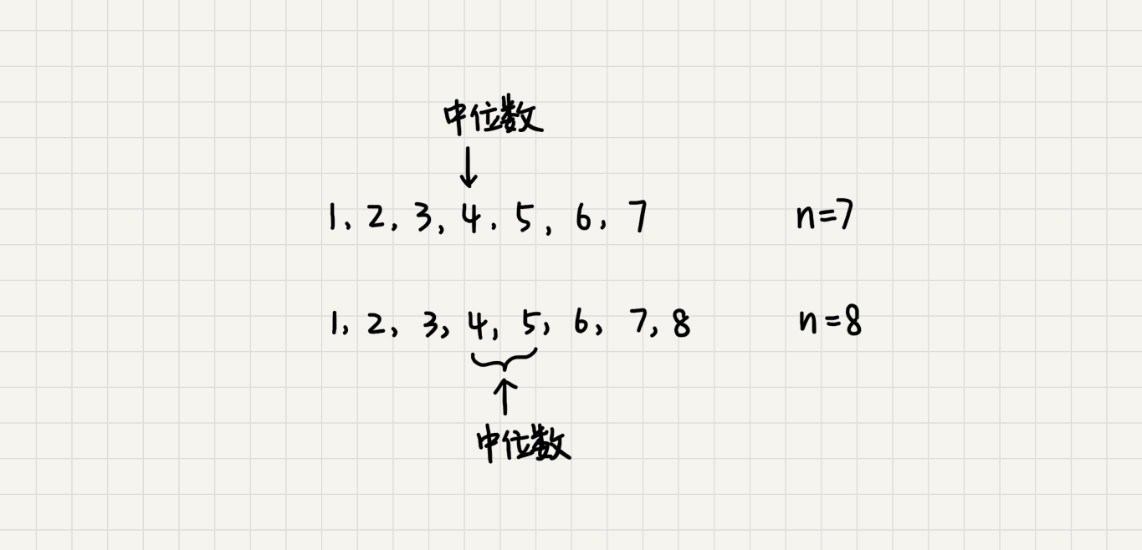
分两种情况:静态数据集合、动态数据集合
对于静态数据,先排序,再取n/2+1。
对于动态数据,如果每次都排序,性能不好。可利用堆来实现。
定义两个堆,一个大顶堆,一个小顶堆。大顶堆存储前半数据,小顶堆存储后半数据,并且小顶堆的数据都大于大顶堆的数据。
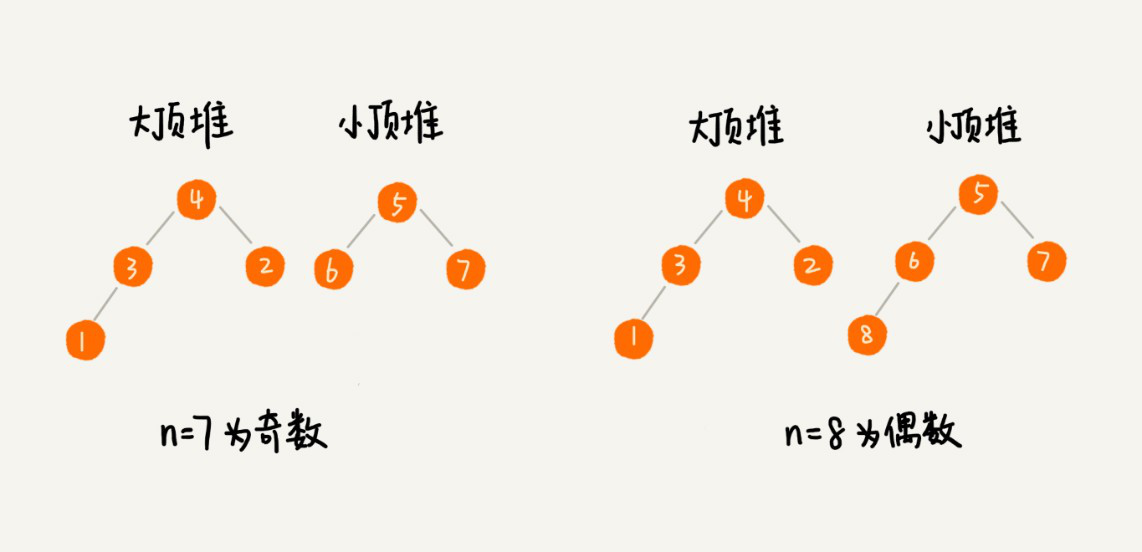
初始化时,对现有数组进行排序,把前n/2(n/2+1)个数存储到大顶堆里,把后n/2个数存储到小顶堆中,中位数就是大顶堆的堆顶。
对于动态插入时,把数据跟大顶堆的堆顶进行比较,如果小于等于堆顶,则插入到大堆顶。如果大于等于小堆顶的堆顶,则插入小堆顶。最后再对大顶堆和小堆顶进行平衡,保证大顶堆是n/2(n/2+1)个数据,小顶堆是n/2个数据。
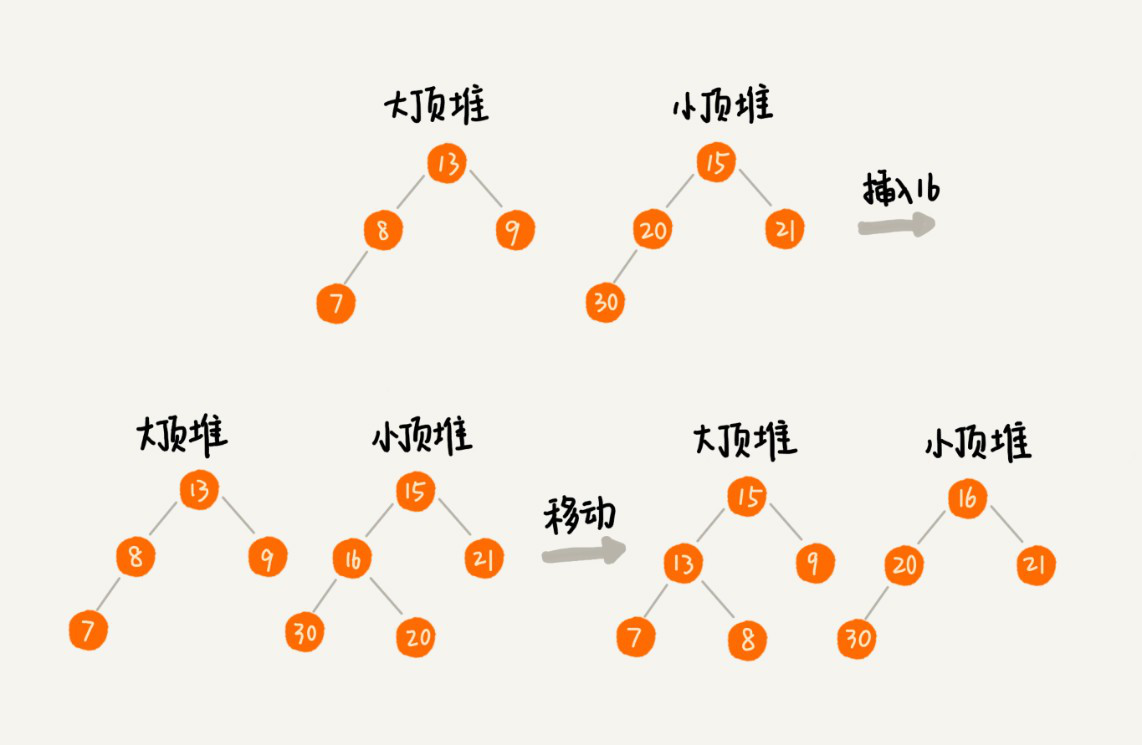
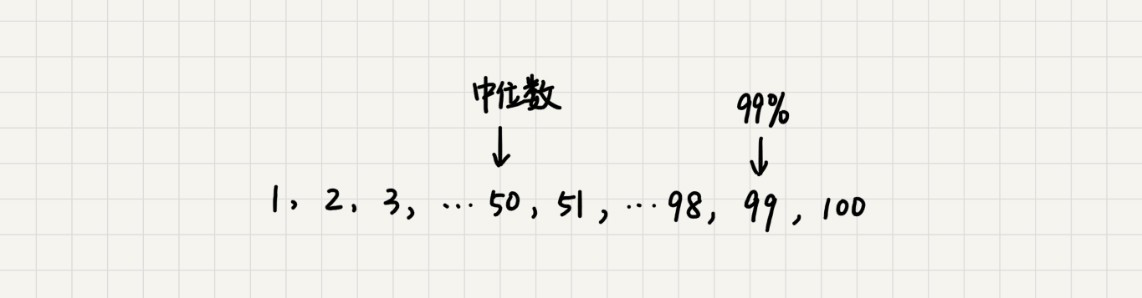
除了求中位数,还能求其他百分位的数据,例如“99%响应时间”。实际上中位数是求50%的数据,大堆顶和小堆顶各占50%,对于“99%响应时间”这个问题,就是把大顶堆划分为99%,小堆顶划分为1%,其他实现跟中位数一样。
时间复杂度:插入数据O(logn)、返回堆顶O(1)