1.Kmeans算法
1.1算法思想
kmeans算法又名k均值算法,是一个重复移动类中心点的过程,把类的中心点,也称重心(centroids),移动到其包含成员的平均位置,然后重新划分其内部成员。k是算法计算出的超参数,表示类的数量;Kmeans可以自动分配样本到不同的类,但是不能决定究竟要分几个类。k必须是一个比训练集样本数小的正整数。有时,类的数量是由问题内容指定的。其算法思想总结为:先从样本集中随机选取 k 个样本作为簇中心,并计算所有样本与这 k 个“簇中心”的距离,对于每一个样本,将其划分到与其距离最近的“簇中心”所在的簇中,对于新的簇计算各个簇的新的“簇中心”。
根据以上描述,我们可以知道实现kmeans算法的要点:
(1)簇个数 k 的选择,一般是按照实际需求进行决定,或在实现算法时直接给定 kk 值。
(2)各个样本点到“簇中心”的距离
给定样本 x(i)={x(i)1,x(i)2,,...,x(i)n,}与x(j)={x(j)1,x(j)2,,...,x(j)n,},其中i,j=1,2,...,m,表示样本数,n表示特征数x(i)={x1(i),x2(i),,...,xn(i),}与x(j)={x1(j),x2(j),,...,xn(j),},其中i,j=1,2,...,m,表示样本数,n表示特 征数 。本文数据集为连续属性,因此代码中主要以欧式距离进行距离的度量计算
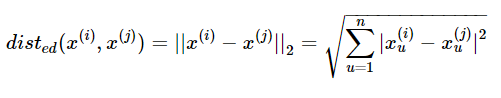
(3)根据新划分的簇,更新“簇中心”
1.2算法步骤
输入:训练数据集 D=x(1),x(2),...,x(m)D=x(1),x(2),...,x(m) ,聚类簇数 k ;
过程:函数 kMeans(D,k,maxIter)kMeans(D,k,maxIter) .
1:从 D 中随机选择 kk 个样本作为初始“簇中心”向量: μ(1),μ(2),...,,μ(k)μ(1),μ(2),...,,μ(k) :
2:repeat
3: 令 Ci=∅(1≤i≤k)Ci=∅(1≤i≤k)
4: for j=1,2,...,mj=1,2,...,m do
5: 计算样本 x(j)x(j) 与各“簇中心”向量 μ(i)(1≤i≤k)μ(i)(1≤i≤k) 的欧式距离
6: 根据距离最近的“簇中心”向量确定 x(j)x(j) 的簇标记: λj=argmini∈{1,2,...,k}djiλj=argmini∈{1,2,...,k}dji
7: 将样本 x(j)x(j) 划入相应的簇: Cλj=Cλj⋃{x(j)}Cλj=Cλj⋃{x(j)} ;
8: end for
9: for i=1,2,...,ki=1,2,...,k do
10: 计算新“簇中心”向量: (μ(i))′=1|Ci|∑x∈Cix(μ(i))′=1|Ci|∑x∈Cix ;
11: if (μ(i))′=μ(i)(μ(i))′=μ(i) then
12: 将当前“簇中心”向量 μ(i)μ(i) 更新为 (μ(i))′(μ(i))′
13: else
14: 保持当前均值向量不变
15: end if
16: end for
17: else
18:until 当前“簇中心”向量均未更新
输出:簇划分 C=C1,C2,...,CK
1.3代码实现

1.4算法优缺点
1.4.1优点:
1.原理比较简单,实现也是很容易,收敛速度快。
2.对大数据集有较高的效率并且是可伸缩性的。
3.主要需要调参的参数仅仅是簇数k。
1.4.2缺点:
1.K值需要预先给定,很多情况下K值的估计是非常困难的。
2.K-Means算法对初始选取的质心点是敏感的,不同的随机种子点得到的聚类结果完全不同 ,对结果影响很大。
3.采用迭代方法,可能只能得到局部的最优解,而无法得到全局的最优解。
参考文献: