


我们分析题目给的条件:在最右边放一个骨牌
我们可以把它转化成:破坏最后的k个骨牌
我们枚举最后一个没被破坏的骨牌在哪,然后模拟把它碰倒,可以二分找到最靠右边的没被破坏的骨牌位置,答案加上被破坏的骨牌数量,再继续此操作
这样时间复杂度O(n^2logn)。
如何优化?
我们用一个数组(d)记录下把第i个位置的骨牌碰倒,会被破坏的骨牌数量(记忆化搜索)
这样我们就可以避免大量的重复计算,这样便可以使时间复杂度优化到O(nlogn)
记得要排序,题目没有说有序

#include<iostream> #include<cstdio> #include<algorithm> #include<cstring> using namespace std; typedef pair<int,int> P; P p[100100];int n,d[100100],ans=999999999; int erfen(int x) { int l=1,r=n+1; while(l<r) { int mid=(l+r)/2; if(p[mid].first>x)r=mid; else l=mid+1; } return l; } int cz(int x) { if(d[x]!=-1)return d[x]; int j=erfen(p[x].first-p[x].second-1)-1; d[x]=cz(j)+x-j-1; return d[x]; } int main() { //freopen("card.in","r",stdin);freopen("card.out","w",stdout); scanf("%d",&n); for(int i=1;i<=n;i++)scanf("%d%d",&p[i].first,&p[i].second); sort(p+1,p+n+1);memset(d,-1,sizeof(d));d[0]=0; for(int i=0;i<=n;i++)ans=min(ans,n-i+cz(i)); printf("%d",ans);return 0; }



我们先证明一个结论:海棠度肯定取相邻的最优。
f(i,j)看起来就像一个斜率
y1=kx1+b
y2=kx2+b
∴k=(y2-y1)/(x2-x1)
由于题目的f函数有加绝对值且i!=j,所以k一定大于0
我们假设有三个点A(x1,y1)B(x2,y2)C(x3,y3)(y1<y2<y3)(x是值,y是下标)
所以它们的图像如下:

AB的斜率或BC的斜率必大于等于AC的斜率(三角形两边之和大于第三边)。就证完啦。
于是,我们把原数组差分。令cf[i]=|a[i+1]-a[i]|,则海棠度(i,j)=max(cf[i~j-1])
我们把每个差分后的值及其坐标形象的在平面直角坐标系中表示出来:
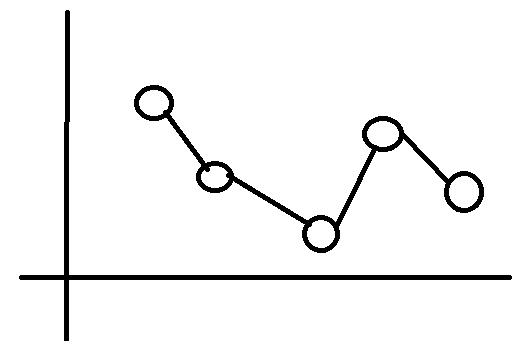
我们发现,每个点(k)对区间[i,j+1](即差分后的区间[i,j])的子区间的海棠度之和的贡献为((k-max(i-1,l))*(min(r,j+1)-k))*cf[k](l表示从k开始最左边的大于cf[k]的数,r表示从k开始最右边的大于cf[k]的数,对于两个一样的数,我们看做下标小的数大(下标大的也行),避免重复计算(一个区间只对应一个最大的数))
根据乘法原理,区间[l,i]的每个数都可以和[i,r]区间的数配对,组成的区间(记为[x,y])中的最大的数(海棠度)为cf[i],保证每个区间不重不漏(因为对于每个区间,有且只有一个最大值)。
那么我们要怎么寻找l,r呢?
单调栈!(不上升)
对于题目要求查询的区间[i,j],我们把cf[i~j-1]按顺序压入栈(为了方便计算,我们先压入一个无穷大的数(下标为i-1)),若一个数被弹出,那么它所对应的l为它上一个数的下标(由于该栈单调不升且我们看做下标小的数大,那么它前一个数一定大于cf[i]且前一个数的下标到i的数不存在比cf[i]大的数(比它大的数都在cf[i]入栈的时候被弹掉了)),所对应的r为压入栈的元素的下标(由于该栈单调不升且我们看做下标小的数大,所以它后面的数(直到压入栈的元素之前)一定小于它),最后我们压入一个无穷大1(下标为j),把栈内元素全部弹出并计算答案
注意开long long,时间复杂度O(nq)

#include<iostream> #include<cstdio> using namespace std; const int INF=1999999999; int n,q,a[100001],cf[100001];int top=0; int st[100101][2];long long ans; int abs(int x){return x>0?x:-x;} int main() { // freopen("array.in","r",stdin);freopen("array.out","w",stdout); scanf("%d%d",&n,&q); for(int i=1;i<=n;i++) { scanf("%d",&a[i]);cf[i-1]=abs(a[i]-a[i-1]); } for(int i=1;i<=q;i++) { int l,r;scanf("%d%d",&l,&r);if(l==r){puts("0");continue;} ans=0;top=0;st[++top][0]=INF;st[top][1]=l-1; int g=cf[r];cf[r]=INF-1; for(int j=l;j<=r;j++) { while(cf[j]>st[top][0]) { ans+=((long long)(st[top][1]-st[top-1][1])*(long long)(j-st[top][1]))*(long long)st[top][0]; top--; } st[++top][0]=cf[j];st[top][1]=j; } cf[r]=g;printf("%lld ",ans); } return 0; }



贪心。我们把a[i]<=b[i]和a[i]>b[i]的数分别按a[i],b[i]排序。
对于a[i]<=b[i]的数,我们按a[i]从小到大依次杀掉每只怪物即可。如果杀不死某只,输出-1。证明:如果你能杀掉a[i]更大的怪物,那么你一定能杀掉这只怪物,而你杀完这只怪物后,再去杀a[i]更大的怪物也行(因为你的血量在杀怪后一定是递增的)。如果你杀不死这只怪物,那么a[i]更大的怪物你更杀不死,所以无解。
对于a[i]>b[i]的数,我们可以计算出玩家杀完所有怪物后最后的HP。我们反过来思考,把b[i]看成扣血,a[i]看成加血。按b[i]从小到大依次杀掉每只怪物。如果你杀不死某只怪物,那么你在吃这个回血之前血量一定<=0。证明与上面一样。注意:由于这种情况我们是倒推过来分析,即分析最后一只要打哪只怪,所以我们输出时对于第一种情况正序输出,对于第二种情况倒序输出
时间复杂度O(nlogn)

#include<iostream> #include<cstdio> #include<algorithm> using namespace std; struct xxx{ int a,b,no; }c[200001],d[200001]; bool cmp1(xxx a,xxx b){return a.a<b.a;} bool cmp2(xxx a,xxx b){return a.b<b.b;} int main() { // freopen("atm.in","r",stdin);freopen("atm.out","w",stdout); int n,h,cc=0,dd=0;scanf("%d%d",&n,&h);int HP=h; for(int i=1;i<=n;i++) { int a,b;scanf("%d%d",&a,&b);HP=HP-a+b; if(a<=b)c[++cc].a=a,c[cc].b=b,c[cc].no=i; else d[++dd].a=a,d[dd].b=b,d[dd].no=i; } if(HP<=0||h<=0){puts("-1");return 0;} sort(c+1,c+cc+1,cmp1);sort(d+1,d+dd+1,cmp2); for(int i=1;i<=cc;i++) { h-=c[i].a;if(h<=0){puts("-1");return 0;}h+=c[i].b; } for(int i=1;i<=dd;i++) { HP-=d[i].b;if(HP<=0){puts("-1");return 0;}HP+=d[i].a; } for(int i=1;i<=cc;i++)printf("%d ",c[i].no); for(int i=dd;i>=1;i--)printf("%d ",d[i].no); return 0; }
