原理:
线段树比树状数组要灵活许多,只要能满足“区间加法”的题,都能用线段树来做。但是对于没有修改的情况,区间和可以用树状数组,Max/Min可以用ST表。
线段树的本质是做区间分解,各个子区间的Sum/Max/Min合成大区间的,例如【2,12】=【2】+【3,4】+【5,7】+【8,10】+【11,12】.
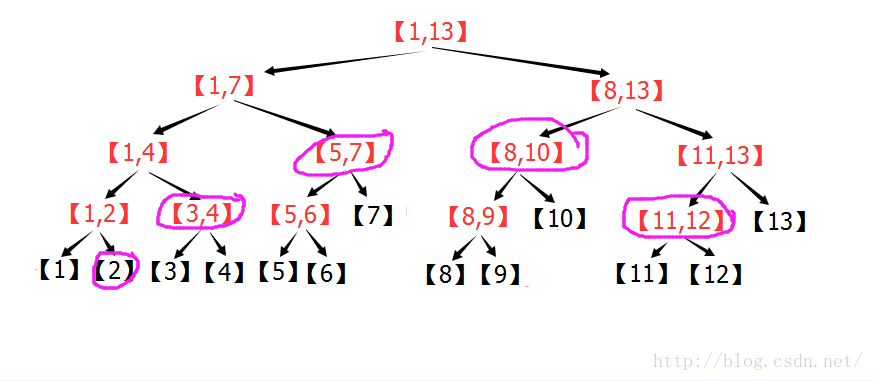
可以证明的是,当n>=3时,[1, n]的任意子区间[l, r] 分解的子区间不超过 2log(n-1)
这样的话,不管是查询还是修改,只需要查询/修改 log(len) 次,而不用 len 次(len是区间长度)。
实现:
建树:可以不用单点修改n次,可以递归到叶子节点,再赋值
单点修改:找到那个点,改掉就可以了
区间修改:不能递归到叶子节点,而是遇到包含在修改范围内的子区间就打上Lazy标记。Update有两种,一种是Add,是个改变量,另一种是Set,是设置为,两者在PushDownh和区间赋值时略有不同
应用:
1. leetcode1526. 形成目标数组的子数组最少增加次数:
dfs(i, j) ,再在线段树上查询[i, j]的最小值
2. leetcode1157. 子数组中占绝大多数的元素:
线段树维护绝对众数,只是区间合并时与普通的不同,采用抵消法
3. leetcode699. 掉落的方块:
维护区间的最大值,由于数值范围过大,需要将所有出现的点进行离散化
4. leetcode1521. 找到最接近目标值的函数值:
二分时,查询[right, mid]的区间与
5. leetcdeo715. Range 模块
区间修改+动态开点,由于数值范围很大,但是又不能离散化(离散化只保留相对顺序,而这里必须修改那么长的区间)
总的来说,就是,要么直接给出左右端点,要么就是dfs/二分/滑动窗口等得到的左右端点,要么范围太大进行离散化/动态开点。
模板:
1. 区间修改(Add)+最小值

struct SegTree { #define maxn 100010 //元素总个数 #define ls l,m,rt<<1 #define rs m+1,r,rt<<1|1 #define INF 0x3f3f3f3f long long Sum[maxn<<2],Add[maxn<<2], Max[maxn<<2], Min[maxn<<2];//Sum求和,Add为懒惰标记, Max区间最大值 // int A[maxn],n;//存原数组数据下标[1,n] vector<int>A; void init(vector<int>& _A){ A = _A; for(int i = 1;i < maxn;i++) Min[i] = INF; } //PushUp函数更新节点信息 ,这里是求和 void PushUp(int rt){ Sum[rt]=Sum[rt<<1]+Sum[rt<<1|1]; Max[rt] = max(Max[rt<<1], Max[rt<<1|1]); // 标记不需要向上维护x Min[rt] = min(Min[rt<<1], Min[rt<<1|1]); // } //Build函数建树 void Build(int l,int r,int rt){ //l,r表示当前节点区间,rt表示当前节点编号 // cout << "build: " << l << " " << r << endl; if(l==r) {//若到达叶节点 Sum[rt]=A[l-1];//储存数组值 Max[rt]=Min[rt]=A[l-1]; return; } int m=(l+r)>>1; //左右递归 Build(l,m,rt<<1); Build(m+1,r,rt<<1|1); //更新信息 PushUp(rt); } void Update(int L,int R,int C,int l,int r,int rt){//L,R表示操作区间,l,r表示当前节点区间,rt表示当前节点编号 // cout << "Update: " << l << " " << r << endl; if(L <= l && r <= R){//如果本区间完全在操作区间[L,R]以内 Sum[rt] +=C*(r-l+1);//更新数字和,向上保持正确 Add[rt] +=C;//增加Add标记,表示本区间的Sum正确,子区间的Sum仍需要根据Add的值来调整 Max[rt] = Max[rt]+C; Min[rt] = Min[rt]+C; return ; } int m=(l+r)>>1; PushDown(rt,m-l+1,r-m);//下推标记 //这里判断左右子树跟[L,R]有无交集,有交集才递归 if(L <= m) Update(L,R,C,l,m,rt<<1); if(R > m) Update(L,R,C,m+1,r,rt<<1|1); PushUp(rt);//更新本节点信息 } void PushDown(int rt,int ln,int rn){ //ln,rn为左子树,右子树的数字数量。 // cout << "rt: " << rt << endl; if(Add[rt]){ //下推标记 Add[rt<<1]+=Add[rt]; Add[rt<<1|1]+=Add[rt]; //修改子节点的Sum使之与对应的Add相对应 Sum[rt<<1]+=Add[rt]*ln; Sum[rt<<1|1]+=Add[rt]*rn; Max[rt<<1] = Max[rt<<1]+Add[rt]; Max[rt<<1|1] = Max[rt<<1|1]+Add[rt]; Min[rt<<1] = Min[rt<<1]+Add[rt]; Min[rt<<1|1] = Min[rt<<1|1]+Add[rt]; //清除本节点标记 Add[rt]=0; } } int Query(int L,int R,int l,int r,int rt){//L,R表示操作区间,l,r表示当前节点区间,rt表示当前节点编号 if(L <= l && r <= R){ //在区间内,直接返回 return Min[rt]; } int m=(l+r)>>1; //下推标记,否则Sum可能不正确 PushDown(rt,m-l+1,r-m); //累计答案 int ANS=INF; if(L <= m) ANS=min(ANS, Query(L,R,l,m,rt<<1)); if(R > m) ANS=min(ANS, Query(L,R,m+1,r,rt<<1|1)); return ANS; } }segTree;
2. 区间修改(Set)+ 最大值
加上离散化,set+unordered_map

class Solution { public: struct SegTree { #define maxn 2010 //元素总个数 #define ls l,m,rt<<1 #define rs m+1,r,rt<<1|1 int Sum[maxn<<2],Add[maxn<<2], Max[maxn<<2];//Sum求和,Add为懒惰标记, Max区间最大值 // int A[maxn],n;//存原数组数据下标[1,n] vector<int>A; void init(vector<int>& _A){ A = _A; } //PushUp函数更新节点信息 ,这里是求和 void PushUp(int rt){ // Sum[rt]=Sum[rt<<1]+Sum[rt<<1|1]; Max[rt] = max(Max[rt<<1], Max[rt<<1|1]); // 标记不需要向上维护 } //Build函数建树 void Build(int l,int r,int rt){ //l,r表示当前节点区间,rt表示当前节点编号 // cout << "build: " << l << " " << r << endl; if(l==r) {//若到达叶节点 // Sum[rt]=A[l-1];//储存数组值 Max[rt]=A[l-1]; return; } int m=(l+r)>>1; //左右递归 Build(l,m,rt<<1); Build(m+1,r,rt<<1|1); //更新信息 PushUp(rt); } void Update(int L,int R,int C,int l,int r,int rt){//L,R表示操作区间,l,r表示当前节点区间,rt表示当前节点编号 if(L <= l && r <= R){//如果本区间完全在操作区间[L,R]以内 // Sum[rt]=C*(r-l+1);//更新数字和,向上保持正确 Add[rt]=C;//增加Add标记,表示本区间的Sum正确,子区间的Sum仍需要根据Add的值来调整 Max[rt] = C; // ** return ; } int m=(l+r)>>1; PushDown(rt,m-l+1,r-m);//下推标记 //这里判断左右子树跟[L,R]有无交集,有交集才递归 if(L <= m) Update(L,R,C,l,m,rt<<1); if(R > m) Update(L,R,C,m+1,r,rt<<1|1); PushUp(rt);//更新本节点信息 } void PushDown(int rt,int ln,int rn){ // ln,rn为左子树,右子树的数字数量。 if(Add[rt]){ //下推标记 Add[rt<<1]=Add[rt]; // ** Add[rt<<1|1]=Add[rt]; // ** //修改子节点的Sum使之与对应的Add相对应 // Sum[rt<<1]+=Add[rt]*ln; // Sum[rt<<1|1]+=Add[rt]*rn; Max[rt<<1] = Add[rt<<1]; // ** Max[rt<<1|1] = Add[rt<<1|1]; // ** //清除本节点标记 Add[rt]=0; } } int Query(int L,int R,int l,int r,int rt){//L,R表示操作区间,l,r表示当前节点区间,rt表示当前节点编号 if(L <= l && r <= R){ //在区间内,直接返回 return Max[rt]; } int m=(l+r)>>1; //下推标记,否则Sum可能不正确 PushDown(rt,m-l+1,r-m); //累计答案 int ANS=0; if(L <= m) ANS=max(ANS, Query(L,R,l,m,rt<<1)); if(R > m) ANS=max(ANS, Query(L,R,m+1,r,rt<<1|1)); return ANS; } }segTree; vector<int> fallingSquares(vector<vector<int>>& positions) { // 维护Max,修改为特定值 // vector<int>vec = {1,4,3,5,2,1,3}; // segTree.init(vec); // segTree.Build(1, vec.size(), 1); // cout << segTree.Query(2,4,1,7,1) << endl; // segTree.Update(1, 3, 1, 1, 7, 1); // segTree.Update(2, 5, 2, 1, 7, 1); // cout << segTree.Query(1,3,1,7,1) << endl; // cout << segTree.Query(1,7,1,7,1) << endl; // 先做个离散化 set<int>st; unordered_map<int, int>mp; int cnt = 1; for(auto position : positions) { int left = position[0], right = position[0]+position[1]; st.insert(left); st.insert(right-1); } for(auto num : st) { mp[num] = cnt++; } // 处理 vector<int>res; int cur_max = -1; for(auto position : positions) { int left = position[0], right = position[0]+position[1]; int max_h = segTree.Query(mp[left], mp[right-1], 1, cnt, 1); segTree.Update(mp[left], mp[right-1], max_h+position[1], 1, cnt, 1); if(max_h+position[1] > cur_max) cur_max = max_h+position[1]; res.push_back(cur_max); } return res; } };
3. 区间修改(Set)+动态开点

/* 动态开点 */ struct SegTree { #define maxn 100010 //元素总个数 int Sum[maxn],Lazy[maxn],Min[maxn];//Sum求和,Add为懒惰标记, Lazy是将改成,Max区间最大值 int ls[maxn], rs[maxn], cnt; // 记录每个点的左右子节点 void init() { for(int i = 0;i < maxn;i++) { Sum[i] = 0,Lazy[i]=0; // if(Lazy[i]) cout << Lazy[i] << endl; } } //PushUp函数更新节点信息 ,这里是求和 void PushUp(int rt){ Sum[rt]=Sum[ls[rt]]+Sum[rs[rt]]; // Max[rt] = max(Max[rt<<1], Max[rt<<1|1]); // 标记不需要向上维护 Min[rt] = min(Min[ls[rt]], Min[rs[rt]]); } //L,R表示操作区间,l,r表示当前节点区间,rt表示当前节点编号 void Update(int L,int R,int C,int l,int r,int& rt) { if(!rt) rt=++cnt; if(L <= l && r <= R){//如果本区间完全在操作区间[L,R]以内 Sum[rt]=C*(r-l+1);//更新数字和,向上保持正确 // Add[rt]=C;//增加Add标记,表示本区间的Sum正确,子区间的Sum仍需要根据Add的值来调整 Min[rt] = C; Lazy[rt] = C; return ; } int m=(l+r)>>1; PushDown(rt,m-l+1,r-m);//下推标记 //这里判断左右子树跟[L,R]有无交集,有交集才递归 if(L <= m) Update(L,R,C,l,m,ls[rt]); if(R > m) Update(L,R,C,m+1,r,rs[rt]); PushUp(rt);//更新本节点信息 } void PushDown(int rt,int ln,int rn){ //ln,rn为左子树,右子树的数字数量。 if(Lazy[rt]){ if(!ls[rt]) ls[rt]=++cnt; if(!rs[rt]) rs[rt]=++cnt; //下推标记 Lazy[ls[rt]] = Lazy[rt]; Lazy[rs[rt]] = Lazy[rt]; //修改子节点的Sum使之与对应的Add相对应 Sum[ls[rt]]=Lazy[rt]*ln; Sum[rs[rt]]=Lazy[rt]*rn; Min[ls[rt]] = Lazy[rt]; Min[rs[rt]] = Lazy[rt]; //清除本节点标记 Lazy[rt]=0; } } int Query(int L,int R,int l,int r,int rt){//L,R表示操作区间,l,r表示当前节点区间,rt表示当前节点编号 if(!rt) return 0; if(L <= l && r <= R){ //在区间内,直接返回 return Sum[rt]; } int m=(l+r)>>1; //下推标记,否则Sum可能不正确 PushDown(rt,m-l+1,r-m); //累计答案 int ANS=0; if(L <= m) ANS+=Query(L,R,l,m,ls[rt]); if(R > m) ANS+=Query(L,R,m+1,r,rs[rt]); return ANS; } }segTree; int n = 1e9+1, root=0;
