多项式大总结

文章没有写完，近期填完这坑

参考文章：

https://www.luogu.com.cn/blog/froggy/duo-xiang-shi-tai-za-hui

https://www.cnblogs.com/zwfymqz/p/8244902.html

https://www.cnblogs.com/RabbitHu/p/FFT.html

https://blog.csdn.net/enjoy_pascal/article/details/81478582

Thomas H.Cormen,Charles E.Leiserson,Ronald L.Rivest,Clifford Stein. 殷建平等译. 算法导论第三版 [M]. 北京:机械工业出版社,2013,527-542.

多项式的定义：

一个 (n) 次多项式，是长成这样的：

[f(x)=sumlimits_{i=0}^n{a_i x^i}quad (a_n eq 0) ]

其中 (a_i) 是第 (i) 项的系数。

拉格朗日插值法：

洛谷模板题

给定 (n) 个点 ((x_i,y_i)) 确定一个多项式 (f(k))，并求出 (f(k)) 的值。

定理：

[f(k)=sum_{i=1}^{n}y_iprod_{j eq i}frac{k-x_j}{x_i-x_j} ]

不会证明这个。

代码：

int n;
ll x[N], y[N], k;
ll ans;

ll qpow(ll a, ll b) 
{
	ll ans = 1;
	for (; b; b >>= 1, a = a * a % mod) 
		if (b & 1) ans = ans * a % mod;
	return ans;
} 

int main()
{
	scanf ("%d%lld", &n, &k);
	for (int i = 1; i <= n; i++)
		scanf ("%lld%lld", &x[i], &y[i]);
	for (int i = 1; i <= n; i++)
	{
		ll tmp = y[i];
		for (int j = 1; j <= n; j++)
			if(i != j)
				tmp = tmp * ((k - x[j] + mod) % mod) % mod * qpow((x[i] - x[j] + mod) % mod, mod - 2) % mod;
		ans = (ans + tmp) % mod;
	}
	printf ("%lld
", ans);
	return 0;
}

快速傅里叶变换 FFT：

为了方便计算，这里的 (n) 都是 (2) 的整次幂。

在此之前，先明白 DFT（离散傅里叶变换）、FFT（快速傅里叶变换）、IDFT（离散傅里叶逆变换）、IFFT（快速傅里叶逆变换） 之间的关系：

类似的，IDFT 也是概念，IFFT 是基于 IDFT 概念的算法。现在不知道这四个东西的具体含义在下文介绍。

洛谷模板题

给定两个多项式 (F(x),G(x))，求出它们的卷积 (F(x)*G(x))。

这里定义多项式卷积运算：

[(F*G)(x)=sum_{i+j=x}F_icdot G_{j} ]

然后快速傅里叶变换可以在 (mathcal{O}(nlog n)) 的时间复杂度内完成多项式乘法。

多项式的点值表示：

点值表示法，顾名思义就是把用 (n) 点的坐标表示一个多项式：

[F(x)={(x_0,F(x_0)),(x_1,F(x_1)),cdots,(x_{n-1},F(x_{n-1}))} ]

而点值表示法的优点就是可以在 (mathcal{O}(n)) 的时间范围内求出两个多项式的乘积。

多项式的系数表示：

系数表示法，就是记录 (F(x)) 每一项的系数，比如 (F(x)=sum_{i=0}^{n-1}a_ix^i) 可以表示为：

[F(x)={a_0,a_1,cdots,a_{n-1}} ]

那么我们可以推测，多项式乘法流程一般是：系数表示法先转化到点值表示法，这样就能快速求卷积，然后由转回系数表示法。也就是有两步，第一步系数转点值就是 DFT；第二步点值转系数 IDFT。

复数：

介绍：

提示：建议学习数学选修 2-2 的复数相关课程。

(i) 是虚数单位，规定：

(i^2=-1)；
实数可以与它进行四则运算，进行四则运算时，原有的加法和乘法运算律仍然成立。

有一个复数 (z=a+bi(a,binmathbb{R}))，其中 (a,b) 分别是 (z) 的实部与虚部。那么在复平面对应的平面直角坐标系中，(z) 在 ((a,b))：

如图点 (Z) 的复数是 (z=3+4i)，它对应的平面直角坐标系中在 ((3,4))。

或者，你还可以把复数作成一个向量：

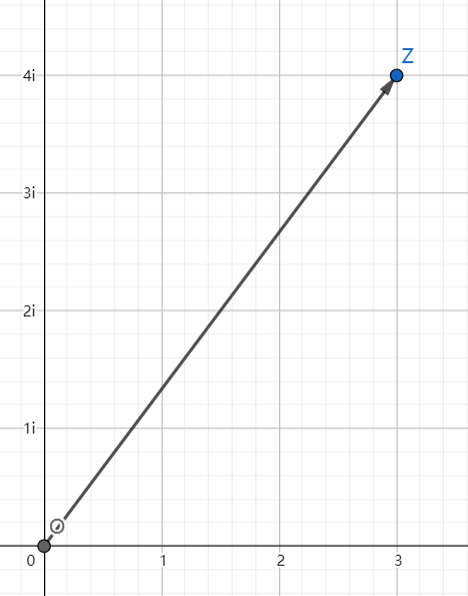
向量 (overrightarrow{OZ}) 与复数 (z=a+bi) 一一对应。然后有：

[|overrightarrow{OZ}|=|z|=|a+bi|=r=sqrt{a^2+b^2}quad(rgeq0,rinmathbb{R}) ]

共轭复数：

一般地，当两个复数的实部相等，虚部互为相反数时，这两个复数叫做互为共轭复数。通常记复数 (z) 的共轭复数为 (overline{z})。

比如当 (z=a+bi) 时，(overline{z}=a-bi)。

复数的运算：

设 (z_1=a+bi,z_2=c+di) 是任意两个复数，那么：

[z_1+z_2=(a+c)+(b+d)i\ z_1z_2=(ac-bd)+(ad+bc)i]

其中，复数相乘时，模长相乘，幅角相加。

DFT：

其实 DFT 的本质就是代入 (x) 得到点值，而这几个 (x) 就是一些特殊的复数（选择这些复数的原因不会证明/youl）。

单位根：

在复平面中，以原点为圆心，半径为 (1) 的圆是 单位圆。然后将这个圆 (n) 等分，以圆心为起点，圆的 (n) 等分点为终点，做 (n) 个向量，设幅角为正且最小的向量对应的复数是 (omega_n)，也就是 (n) 次单位根。根据复数乘法性质，剩下 (n-1) 个复数是 (omega_n^2,omega_n^3,dots,omega_n^n)。其中，这几个复数的值是：

[omega_n^k=cos kcdotfrac{2pi}{n}+isin kcdotfrac{2pi}{n} ]

这几个复数就是那几个 “特殊的复数”。

单位根的性质：

性质一：

[omega_{n}^{k}=omega_{2n}^{2k} ]

证明：

[omega_{n}^{k}=cos kcdotfrac{2pi}{n}+isin kcdotfrac{2pi}{n}=cos 2kcdotfrac{2pi}{2n}+isin 2kcdotfrac{2pi}{2n}=omega_{2n}^{2k} ]

性质二：

[omega_{n}^{k + frac{n}{2}} = -omega_{n}^{k} ]

证明：

[egin{aligned}omega_{n}^{frac{n}{2}}&=cos frac{ncdot2pi}{2n}+isinfrac{ncdot2pi}{2n}\&=cospi+isinpi\&=-1end{aligned} ]

FFT 的流程：

朴素的 DFT 是 (mathcal{O}(n^2)) 的，通过分治优化 DFT 得到 FFT。

设多项式 (F(x)=a_0+a_1x+a_2x^2+cdots+a_{n-1}x^{n-1})，然后按照奇偶性分为两份：

[egin{aligned}F(x)&=(a_0+a_2x^2+cdots+a_{n-2}x^{n-2})+(a_1x+a_3x^3+cdots+a_{n-1}x^{n-1})\ &=(a_0+a_2x^2+cdots+a_{n-2}x^{n-2})+x(a_1+a_3x^2+cdots+a_{n-1}x^{n-2})end{aligned}]

设：

[F_1(x)=a_0+a_2x+a_4x^2+cdots+a_{n-2}x^{frac{n}{2}-1}\ F_2(x)=a_1+a_3x+a_5x^2+cdots+a_{n-1}x^{frac{n}{2}-1}]

那么：

[F(x)=F_1(x^2)+xcdot F_2(x^2) ]

将 (x=omega_n^kquad(k<frac{n}{2})) 代入得：

[egin{aligned}F(omega_n^k)&=F_1(omega_n^{2k})+omega_n^kcdot F_2(omega_n^{2k})\ &=F_1(omega_{frac{n}{2}}^{k})+omega_n^kcdot F_2(omega_{frac{n}{2}}^{k}) end{aligned}]

将 (x=omega_n^{k+frac{n}{2}}) 代入得：

[egin{aligned}F(omega_n^{k+frac{n}{2}})&=F_1(omega_n^{2k+n})+omega_n^{k+frac{n}{2}}cdot F_2(omega_n^{2k+n})\ &=F_1(omega_n^{2k}cdotomega_n^n)+omega_n^{k+frac{n}{2}}cdot F_2(omega_n^{2k}cdotomega_n^n)\ &=F_1(omega_{frac{n}{2}}^{k})-omega_n^{k}cdot F_2(omega_{frac{n}{2}}^{k})\ end{aligned}]

然后我们就可以通过 (mathcal{O}(nlog n)) 的时间复杂度递归了。

IFFT 的流程：

我们得到了点值表示 (F(x)={(omega_n^0,F(omega_n^0)),(omega_n^1,F(omega_n^1)),cdots,(omega_n^{n-1},F(omega_n^{n-1}))})。设：(y_k=sum_{i=0}^{n-1}a_icdotomega_n^{ki})，我们要求系数：

[a_i=frac{1}{n}sum_{j=0}^{n-1}y_jcdotomega_n^{-ij} ]

关于证明，stoorz 爷的看法：

QuantAsk 爷的看法：

虽然二位爷都对我进行嘲讽，但这不影响我们证明。

将 (y_i) 的定义代入后面的和式得到：

[sum_{j=0}^{n-1}sum_{k=0}^{n-1}a_kcdotomega_n^{kj}cdotomega_n^{-ij}=sum_{j=0}^{n-1}sum_{k=0}^{n-1}a_kcdotomega_n^{(k-i)j}=sum_{k=0}^{n-1}a_kcdotsum_{j=0}^{n-1}omega_n^{(k-i)j} ]

发现最后的和式是等比数列求和。设 (S(omega_n^k)=sum_{i=0}^{n-1}(omega_n^k)^iquad(k>0))，用等比数列求和公式代入：

[egin{aligned}S(omega_n^k)&=frac{(omega_n^k)^n-1}{omega_{n}^{k}-1}\ &=frac{(omega_n^n)^k-1}{omega_{n}^{k}-1}\ &=frac{1-1}{omega_{n}^{k}-1}end{aligned}]

而 (S(omega_n^0)) 更好求了：

[S(omega_n^0)=sum_{i=0}^{n-1}(omega_n^0)^i=sum_{i=0}^{n-1}1=n ]

代回原式：

[sum_{k=0}^{n-1}a_kcdot S(omega_n^{k-i})=sum_{k=0}^{n-1}a_kcdot n[k=i]=a_icdot n ]

(a_i=frac{1}{n}sum_{j=0}^{n-1}y_jcdotomega_n^{-ij}) 得证。

所以 IFFT 只用用对点值表示的 (F(x)) 像 FFT 一样操作，只不过乘的是原来的复数的共轭，就可以求出系数表示的多项式了。

蝴蝶变换优化：

递归 FFT 常数大，所以尝试把它变成迭代形式。

按奇偶性划分可以发现一个规律：

十进制	二进制
(0~1~2~3~4~5~6~7)	(000~001~010~011~100~101~110~111)
(0~2~4~6,1~3~5~7)	(000~010~100~110,001~011~101~111)
(0~4,2~6,1~5,3~7)	(000~100,010~110,001~101,011~111)
(0,4,2,6,1,5,3,7)	(000,100,010,110,001,101,011,111)

每一个数最终的位置，就是把它的二进制翻转过来。

所以每个数的位置就能够 (mathcal{O}(n)) 预处理出来（递推式见代码 tr[i])。

代码：

const int N = 1500010;

const double PI = acos(-1.0);

struct Complex
{
	double x, y;
	Complex (double ix, double iy) {x = ix, y = iy;}
	Complex () {x = y = 0;}
	Complex operator + (Complex &b) 
	{
		return Complex(x + b.x, y + b.y);
	}
	Complex operator - (Complex &b) 
	{
		return Complex(x - b.x, y - b.y);
	}
	Complex operator * (Complex &b) 
	{
		return Complex(x * b.x - y * b.y, x * b.y + y * b.x);
	}
	
}f[N << 1], g[N << 1];

int n, m;
int tr[N << 1];

void FFT (Complex *f, bool isDFT)
{
	for (int i = 1; i <= n; i++)
		if (i < tr[i]) swap (f[i], f[tr[i]]);
	
	for (int p = 2; p <= n; p <<= 1)
	{
		int len = p >> 1;
		Complex omega(cos(2 * PI / p), sin(2 * PI / p));
		if (!isDFT) omega.y *= -1;                  //共轭复数 
		for (int k = 0; k < n; k += p)
		{
			Complex tmp(1, 0);
			for (int i = k; i < k + len; i ++)
			{
				Complex y = tmp * f[i + len];
				f[i + len] = f[i] - y;
				f[i] = f[i] + y;
				tmp = tmp * omega;
			}
		}
	}
    if(!isDFT) for (int i = 0; i <= n; i++) f[i].x /= n;
}

int main()
{
	scanf ("%d%d", &n, &m);
	for (int i = 0; i <= n; i++)
		scanf ("%lf", &f[i].x);
	for (int i = 0; i <= m; i++)
		scanf ("%lf", &g[i].x);
		
	for (m += n, n = 1; n <= m; n <<= 1);
	for (int i = 1; i <= n; i++)
		tr[i] = (tr[i >> 1] >> 1) | (i & 1? n >> 1: 0);
	
	FFT(f, 1), FFT(g, 1);
	
	for (int i = 0; i <= n; i++) f[i] = f[i] * g[i];
		
	FFT(f, 0);
	for (int i = 0; i <= m; i++)
		printf ("%d ", (int)(f[i].x + 0.49));
	return 0;
}

快速数论变换 NTT：

由于 FFT 会有很大的精度误差，所以用模数操作代替，就是 NTT 了，NTT 也比 FFT 要快很多。

原根的定义：

百度百科给的定义：
原根是一种数学符号，设 (p) 是正整数，(g) 是整数，若 (g) 模 (p) 的阶等于 (varphi(p))，则称 (g) 为模 (p) 的一个原根。

简单点说：

若整数 (g) 是奇素数 (p) 的一个原根，则满足 (g,g^2,g^3,cdots,g^{p-1}) 在模 (p) 意义下互不相同。

在模 (998244353) 意义下最小原根 (g=3)!

NTT 的基本流程：

若 (p) 满足 (2^kcdot r+1)（比如 (998244353=2^{23} imes199+1)），把 (g^{frac{p-1}{2^k}}) 作为 (omega_n^1)，发现原本单位根的性质它都能满足，那么就这么跑 FFT 可以了。

但 NTT 也有局限性，只能处理 (nleq 2^k) 的情况，遇到模数 (p=10^9+7) 时，NTT 就做不了。所以后面有任意模数 NTT。

代码：

const int N = 1500010;

const ll mod = 998244353ll, G = 3, invG = 332748118ll;

ll f[N << 1], g[N << 1];

int n, m;
int tr[N << 1];

ll qpow(ll a, ll b)
{
	ll ans = 1;
	for (; b; b >>= 1, a = a * a % mod)
		ans = ans * (b & 1? a: 1) % mod;
	return ans;
}

void NTT (ll *f, bool isDFT)
{
	for (int i = 1; i <= n; i++)
		if (i < tr[i]) swap (f[i], f[tr[i]]);
	
	for (int p = 2; p <= n; p <<= 1)
	{
		int len = p >> 1;
		ll omega = qpow(isDFT? G: invG, (mod - 1) / p);
		for (int k = 0; k < n; k += p)
		{
			ll tmp = 1ll;
			for (int i = k; i < k + len; i ++)
			{
				ll y = tmp * f[i + len] % mod;
				f[i + len] = (f[i] - y + mod) % mod;
				f[i] = (f[i] + y) % mod;
				tmp = tmp * omega % mod;
			}
		}
	}
    if(!isDFT) 
	{
		ll invn = qpow(n, mod - 2);
		for (int i = 0; i <= n; i++) f[i] = f[i] * invn % mod;
	}
}

int main()
{
	scanf ("%d%d", &n, &m);
	for (int i = 0; i <= n; i++)
		scanf ("%lld", &f[i]);
	for (int i = 0; i <= m; i++)
		scanf ("%lld", &g[i]);
		
	for (m += n, n = 1; n <= m; n <<= 1);
	for (int i = 1; i <= n; i++)
		tr[i] = (tr[i >> 1] >> 1) | (i & 1? n >> 1: 0);
	
	NTT(f, 1), NTT(g, 1);
	
	for (int i = 0; i <= n; i++) f[i] = f[i] * g[i];
		
	NTT(f, 0);
	for (int i = 0; i <= m; i++)
		printf ("%lld ", f[i]);
	return 0;
}

多项式乘法逆：

洛谷模板题

给定一个多项式 (F(x)) ，请求出一个多项式 (G(x))，满足 (F(x) * G(x) equiv 1pmod{x^n})。系数对 (998244353) 取模。

思路：

运用倍增的思想求解。

设已经求出 (G'(x)equiv F(x)^{-1}pmod{x^{frac{n}{2}}})，将 (G(x)equiv F(x)^{-1}pmod{x^n}) 与之相减得：

[G(x)-G'(x)equiv 0pmod{x^{frac{n}{2}}} ]

式子两边同时取平方：

[G(x)^2-2cdot G(x)cdot G'(x)+G'(x)^2equiv 0pmod{x^n} ]

式子两边同时乘 (F(x)):

[egin{aligned}G(x)-2cdot G'(x)+G'(x)^2cdot F(x)&equiv 0&pmod{x^n}\ G(x)&equiv 2cdot G'(x)-G'(x)^2cdot F(x)&pmod{x^n} end{aligned}]

接着就可以套 NTT 求解了。

代码：

const int N = 1500010;

const ll mod = 998244353ll, G = 3, invG = 332748118ll;

ll f[N << 1], g[N << 1];

int n, m;
int tr[N << 1];

ll qpow(ll a, ll b)
{
	ll ans = 1;
	for (; b; b >>= 1, a = a * a % mod)
		ans = ans * (b & 1? a: 1) % mod;
	return ans;
}

void NTT (ll *f, bool isDFT, int n)
{
	for (int i = 1; i <= n; i++)
		if (i < tr[i]) swap (f[i], f[tr[i]]);
	
	for (int p = 2; p <= n; p <<= 1)
	{
		int len = p >> 1;
		ll omega = qpow(isDFT? G: invG, (mod - 1) / p);
		for (int k = 0; k < n; k += p)
		{
			ll tmp = 1ll;
			for (int i = k; i < k + len; i ++)
			{
				ll y = tmp * f[i + len] % mod;
				f[i + len] = (f[i] - y + mod) % mod;
				f[i] = (f[i] + y) % mod;
				tmp = tmp * omega % mod;
			}
		}
	}
    if(!isDFT) 
	{
		ll invn = qpow(n, mod - 2);
		for (int i = 0; i <= n; i++) f[i] = f[i] * invn % mod;
	}
}

ll h[N << 1];

void Inv(ll *f, ll *g, int m)
{
	if (m == 1)
	{
		g[0] = qpow(f[0], mod - 2);
		return ;
	}
	Inv(f, g, (m + 1) / 2);
	int n;
	for (n = 1; n < (m << 1); n <<= 1);
	for (int i = 0; i <= n; i++)
		tr[i] = (tr[i >> 1] >> 1) | (i & 1? n >> 1: 0),
		h[i] = f[i] * (i <= m);
	
	NTT(h, 1, n), NTT(g, 1, n);
	
	for (int i = 0; i <= n; i++) 
		g[i] = (2 - g[i] * h[i] % mod + mod) % mod * g[i] % mod;
		
	NTT(g, 0, n);
	
	for (int i = m; i <= n; i++) g[i] = 0;
}

int main()
{
	scanf ("%d", &n);
	for (int i = 0; i < n; i++)
		scanf ("%lld", &f[i]);
	Inv(f, g, n);
	for (int i = 0; i < n; i++)
		printf ("%lld ", g[i]);
	return 0;
}

多项式对数函数：

洛谷模板题

给定一个多项式 (F(x)) ，请求出一个多项式 (G(x))，满足 (G(x) equiv ln F(x)pmod{x^n})。系数对 (998244353) 取模。

求导：

提示：建议学习数学选修 2-2 的导数相关课程。

瞬时变化率：

先咕到这罢!

相关阅读:
4、[重点]Mybatis配置解析
 3、Mybatis的CRUD实现
 mybatis程序容易出错的地方
 1、初识Mybatis
容易忽略的基础
 读取.properties配置文件的几种方式：
格式化数字显示
 安装ipa文件
 保活一个线程
 地图经纬度的问题
原文地址：https://www.cnblogs.com/GJY-JURUO/p/14352531.html