求中位数


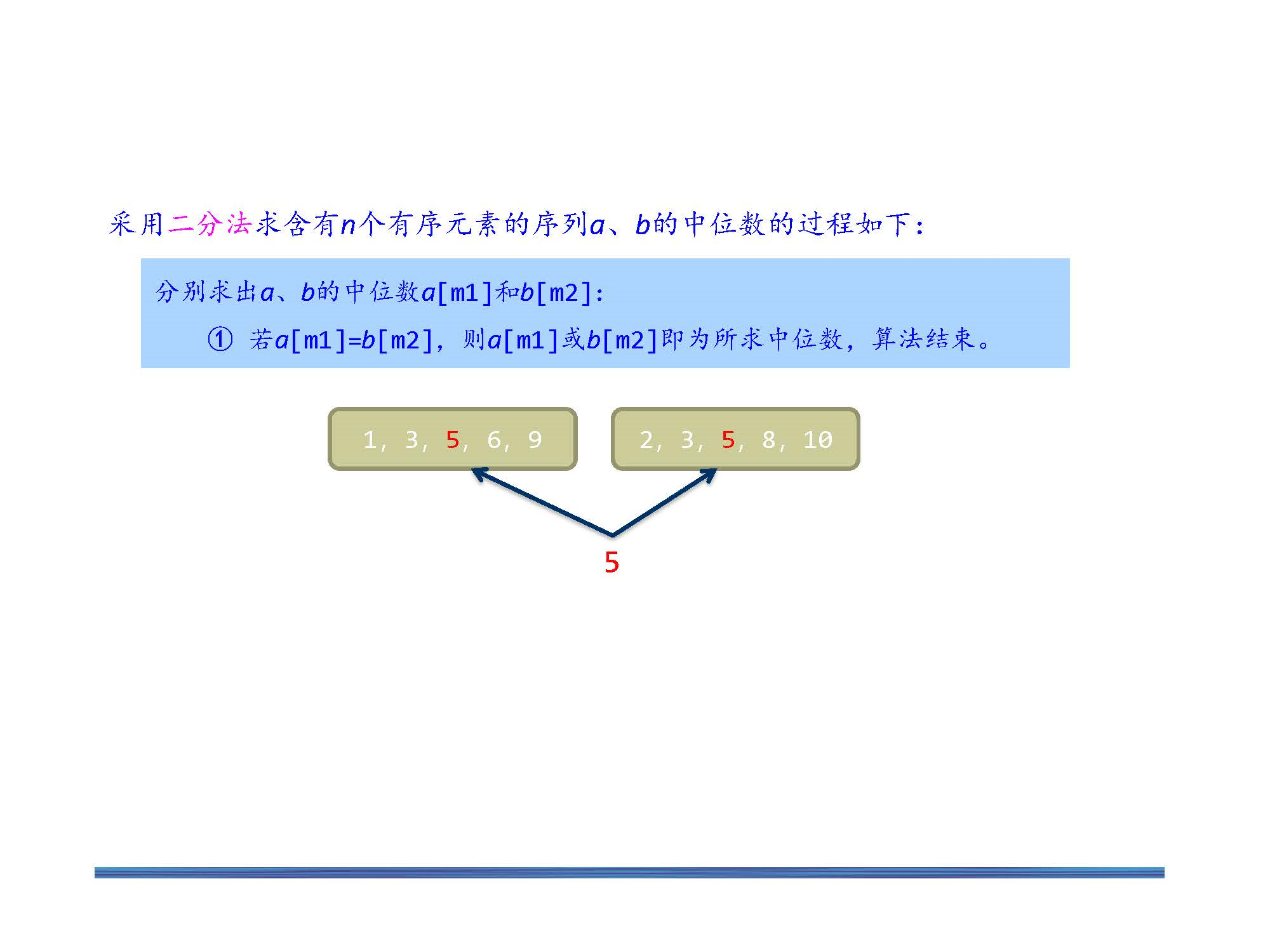


求K-th(leetcode4)
由于上面的写法要求两个数组等长且是奇数,leetcode上的题长度不定,所以按中位数的写法并不好写。
如果我们能用log的复杂度找到第K个,那么很容易得到中位数.
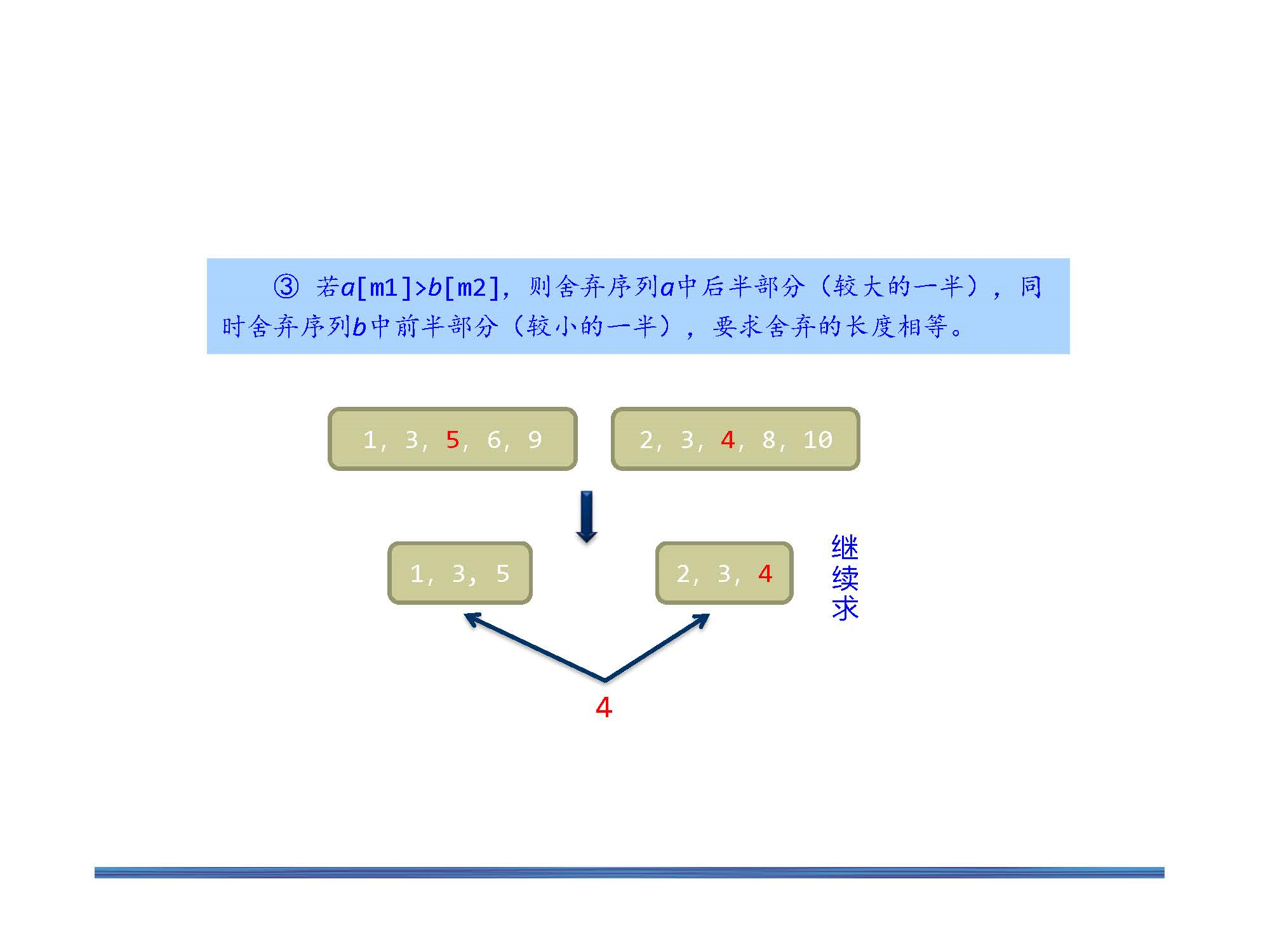
方法大致如下:从两个数组取前K/2个,比较两部分的第K/2个,将较小的那部分去掉,在剩下的部分找K-K/2个,这就是个递归了。
class Solution { private: int INF = 0x3f3f3f3f; public: double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) { int m = nums1.size(), n = nums2.size(); if(m == 0) { if(n&1) return nums2[n/2]; return (nums2[n/2-1] + nums2[n/2])*1.0 / 2; } if(n == 0) { if(m&1) return nums1[m/2]; return (nums1[m/2] + nums1[m/2-1])*1.0 / 2; } int th = (m+n+1)/2, th2 = (m+n+2)/2; return (find_kth(nums1, 0, nums2, 0, th) + find_kth(nums1, 0, nums2, 0, th2))/2; } double find_kth(vector<int>a, int sa, vector<int>b, int sb, int k) { if(sa > a.size()-1) return b[sb+k-1]; if(sb > b.size()-1) return a[sa+k-1]; if(k == 1) return min(a[sa], b[sb]); int mid_a = INF, mid_b = INF; if(sa + k/2-1 < a.size()) mid_a = a[sa + k/2-1]; if(sb + k/2-1 < b.size()) mid_b = b[sb + k/2-1]; if(mid_a < mid_b) return find_kth(a, sa+k/2, b, sb, k-k/2); else return find_kth(a, sa, b, sb+k/2, k-k/2); } };
参考链接:
1. https://blog.csdn.net/qq_14821023/article/details/50806849
2. 《算法设计与分析》-董老师的PPT