问题
对于任意的闭合环路，是否总能在其上找到四个点形成一个矩形？
该问题也被称为内接矩形问题，而内接正方形问题至今没有解答方案。
首先我们不再关注单个而是成对的点，并利用矩形的性质：对于平面上任意两对不同的点 a，c 和 b，d ，只需确保它们有相同的中点，且 a，c 间的距离等于 b，d 点的距离，那么即可以保证这四个点可以组成矩形。这样寻找闭合环路内接矩形问题就转化为了寻找两对点的问题。
我们定义一个函数$f(A,B) = (x,y,z)将环路的上的点对（无序）映射到三维空间上的一个点
设闭合回路位于3维空间中的X-Y平面上，对于给定的一对点，取中点记为M，AB间距离为d，将位于M上方d个单位的点画出：
对环路上的所有点对进行同样的操作，则在平面上方画出了某种曲面：
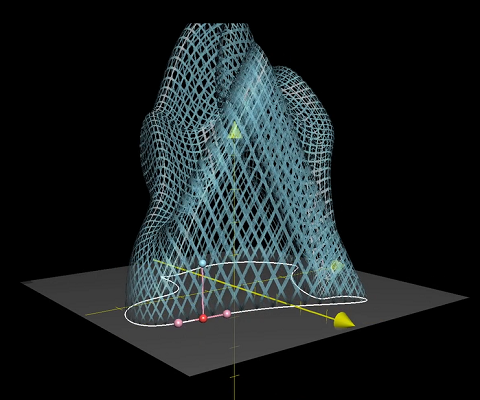
注意一点重要的性质
$$f(x,x) = x$$
即该曲面一定以环路为底，同时曲面必定连续。
我们的目标即是要证明这一曲面存在碰撞，即有两对不同的点对被映射到同一点。
下一步，我们需要找到一个二维曲面，与环路上的点对存在一 一对应关系。
点对可以分为两种：有序对$(a,b) eq (b,a)$和无序对$(a,b)=(b,a)$
首先寻找有序对所对应的自然形状:
- 将环路在某一点切开并拉直为[0,1]区间的X轴，再用一个区间构成Y轴，这样在[0,1]x[0,1]上的单位正方形中的点对应环路上的一对点
- 由于在正方形边界上存在重复对应的点对（这是因为0和1是同一点），因此将正方形的左右边界进行粘贴，再对上下边界进行粘贴，即得到一个环面
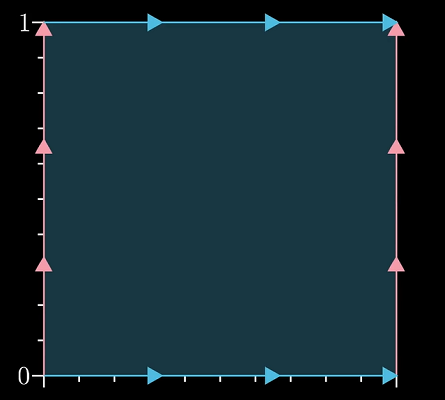
- 该表面上的每个点都与环路上的有序对一一对应
无序对：
- 由于正方形上的点关于$y=x$对称，先将其沿对角线对折成三角形。
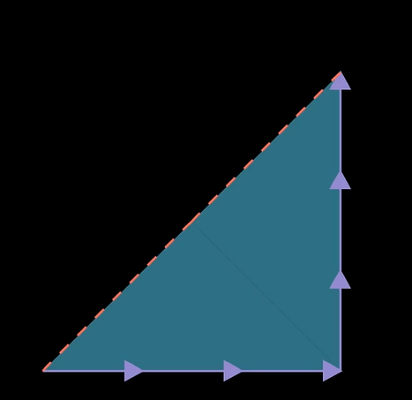
- 需要将三角形的下边界粘贴到右边界，此时注意粘贴的方向性。首先沿对角线切开，将其中一个小三角形进行翻转并重新拼接成为一个小正方形
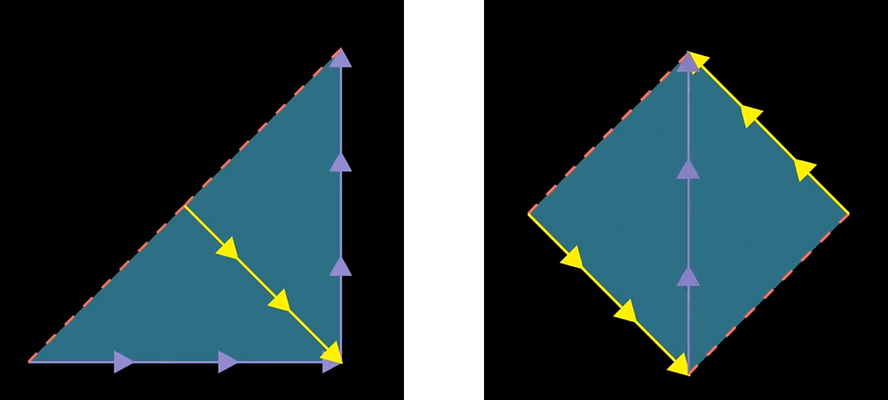
- 需要将该正方形的黄色边界再次粘贴，得到莫比乌斯带，该表面上的每一个点都与环路上的无序对一 一对应
注意到莫比乌斯带的红色边界对应的是$(x,x)$这样的点对 - 得到平面上的无序点对所对应的自然形状是莫比乌斯带这一结论后，自然存在莫比乌斯带到三维曲面的一个映射（其实 这三者相互一一对应），而该映射又必须保证莫比乌斯带的边界正好映射到平面上的环路。由于莫比乌斯带的特殊形状，将它的边界粘到二维平面必定会使其自身相交（即莫比乌斯带上不同的两点对应三维曲面上的同一点），原命题得证。
参考链接：