前言:前面介绍的线性表的顺序存储结构和链式存储结构中,都有对对象地引用或指向,也就是编程语言中有引用或者指针,那么在没有引用或指针的语言中,该怎么实现这个的数据结构呢?
一、简介
定义:用数组代替指针或引用来描述单链表,即用数组描述的链表叫做静态链表,这种描述方法叫做游标实现法;
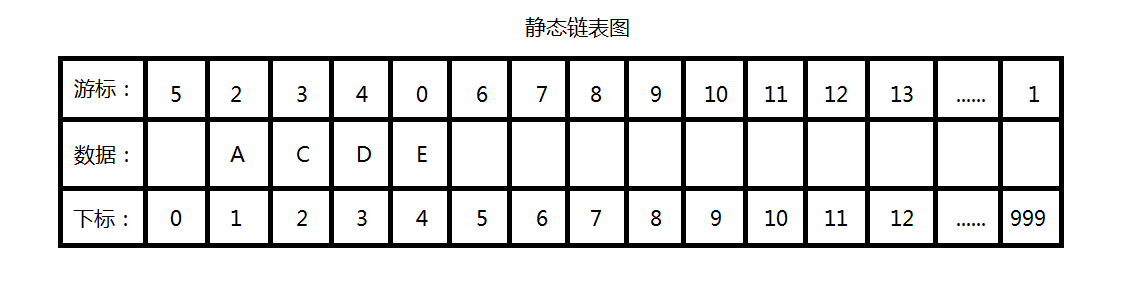

上面的静态链表图有两个数组游标和数据,其中数据数组存储数据,而游标数组存储同下标为数据的下一个数据的下标值,简单模拟一下静态链表遍历的过程:
- 先查看下标为999的游标数组值:1;
- 根据游标数组值1,查找下标为1的数据:A;
- 然后查看游标数组为1的值:2;
- 根据游标数组值为2查找对应的数据数组的值:C;
- 然后循环3->4,直至游标数组的值为0;
二、代码实现
静态链表的创建:
- 我们对数组的第一个和最后一个元素做特殊处理,他们的data不存放数据;
- 我们通常把未使用的数组元素称为备用链表;
- 数组的第一个元素,即下标为0的那个元素的cur就存放备用链表的第一个结点的下标;
- 数组的最后一个元素,即下标为MAXSIZE-1的cur则存放第一个有数值的元素的下标,相当于单链表中的头结点作用;
静态链表创建代码实现:
public class StaticChain<T> { //数据链 private T[] datas; //游标链 private int[] vernier; private Integer size; private Integer length = 1000; StaticChain() { datas = (T[])new Object[length]; vernier = new int[length]; //将游标链的末位(头结点)初始化为1(下一节点的位置) vernier[length-1]=1; //将游标链的首位(空闲位的位置)初始化为1 vernier[0]=1; size = 0; } }
插入操作:
1、获取游标链下标为0的值为空闲位置的下标,并将该值对应下标所在的值放在游标链下标为0的地方;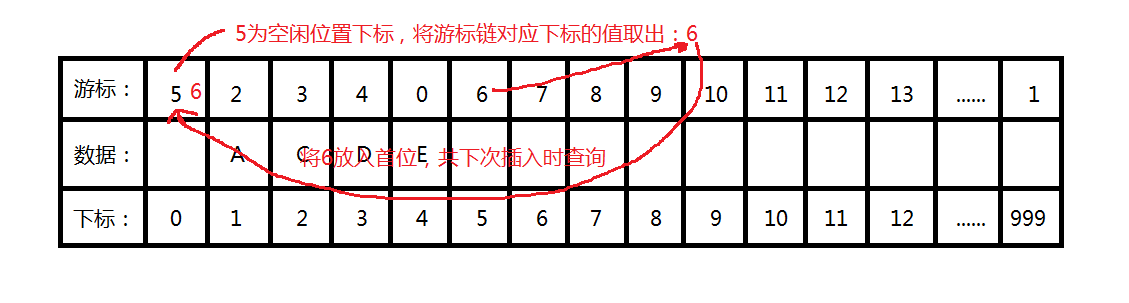
2、在5的位置插入值F,并将下标为5的游标链的值修改为0;
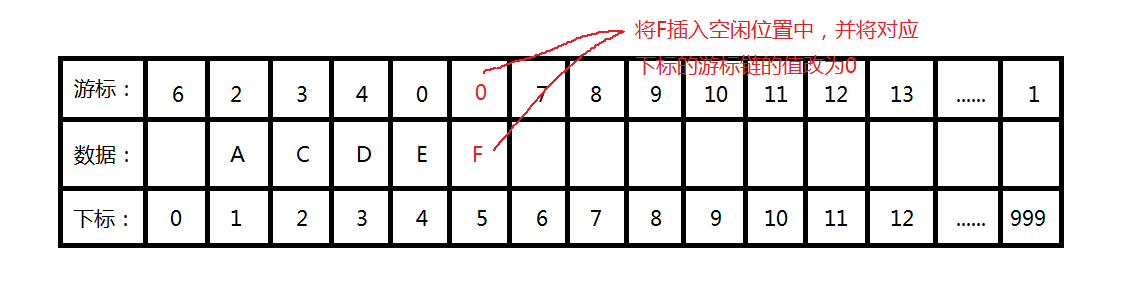
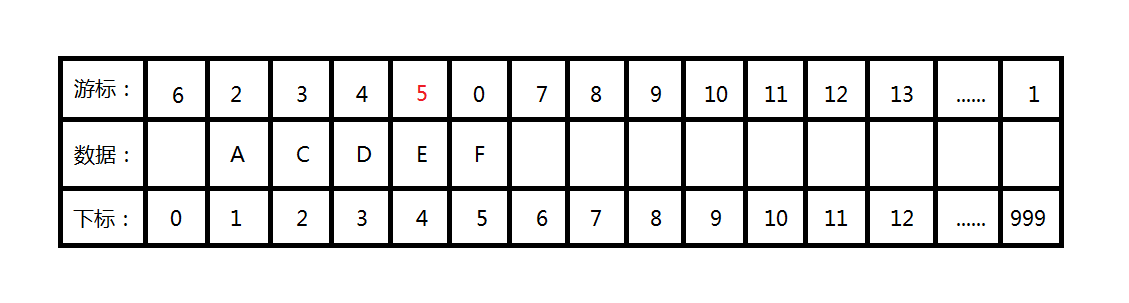
3、若插入值为末位则直接将对应下标为4的游标链的值改为5,否则循环查找要插入值的上一位,并对应下标为4的游标链的值改为5;

插入操作代码如下:

//插入到第几个元素的后面 public void add(Integer index,T t) throws Exception { if (index>size) throw new Exception("outof index"); int insertIndex = vernier[0]; if (index == size) { int freeIndex = vernier[insertIndex]; //将空闲位置的下标放入游标链的首位 vernier[0] = freeIndex; //将刚插入末位值对应下标的游标链的值置为0 vernier[insertIndex] = 0; //将值插入对应的位置 datas[insertIndex] = t; //获取第几个元素的游标链对应的值 Integer preIndex = this.getIndex(index); //将上一个元素的游标链的值改为插入的值的下标 vernier[preIndex] = insertIndex; size++; } else { //获取第index+1个元素的游标链对应的值 Integer nextIndex = this.getIndex(index+1); //将插入位置下标对应的游标链的值改为下一个元素的位置 vernier[insertIndex] = vernier[nextIndex]; datas[insertIndex] = t; //将上一个元素的游标链的值改为插入的值的下标 Integer preIndex = this.getIndex(index); vernier[preIndex] = insertIndex; size++; //重置游标链的首位为空闲值下标 Integer endIndex = this.getIndex(size); vernier[0] = vernier[endIndex]; vernier[endIndex] = 0; } } //查询几个元素的游标链对应的下标 private Integer getIndex(Integer index) throws Exception { int k = length - 1; for (int i = 1; i <= index; i++) k = vernier[k]; if (k==-1) { throw new Exception("outof index"); } return k; }
删除操作:
1、查找到要删除的节点的下标,将其对应的游标链的值取出来放在上一个游标链的指;
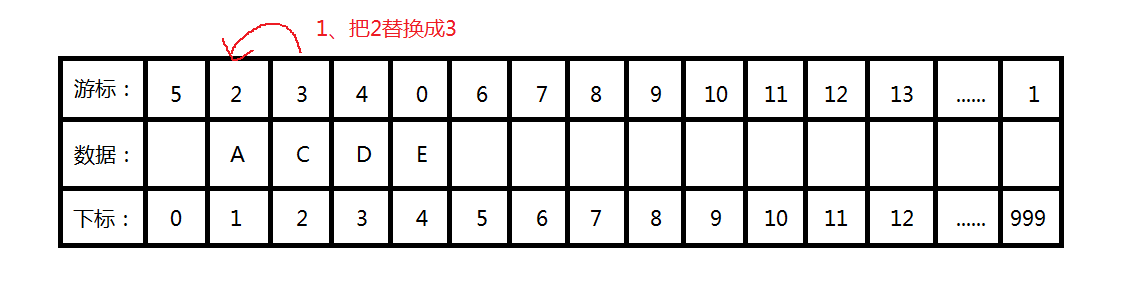

2、并将删除的结点对应的游标链的值改为当前空闲指的下标,将空闲值的下标改为当前删除节点的下标;
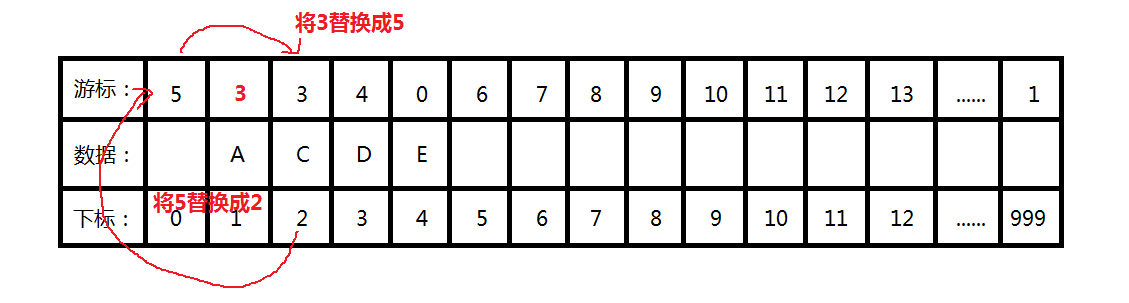

删除操作代码如下:
//删除第index个元素 public T remove(Integer index) throws Exception { T data = null; if (index == 1) { Integer delIndex = vernier[999]; data = datas[delIndex]; int nextIndex = vernier[delIndex]; vernier[length-1] = nextIndex; vernier[delIndex] = vernier[0]; vernier[0] = delIndex; } else { Integer delIndex = this.getIndex(index); data = datas[delIndex]; int nextIndex = vernier[delIndex]; Integer preIndex = this.getIndex(index - 1); vernier[preIndex] = nextIndex; vernier[delIndex] = vernier[0]; vernier[0] = delIndex; } return data; }
三、总结
优点:
- 在插入和删除操作时,只需要修改游标,不需要移动元素,从而改进了在顺序存储结构中的插入和删除操作需要移动大量元素的缺点;
- 解决了在某些没有引用和指针的高级语言中无法创建线性表的链式存储结构;
缺点:
- 没有解决连续存储分配(数组)带来的表长难以确定的为题;
- 失去了顺序存储结构随机存取的特性;
在这里就要说一下静态链表和动态链表的区别:
- 静态链表是数组实现的,是顺序存储结构,在物理地址上是连续的,而且需要预先分配大小。而动态链表适用内存申请函数(malloc)动态申请内存的,所以每个节点的物理地址是不连续的,要通过指针来顺序访问;
- 静态链表的大小是一开始就定好的,所以当数组放满后就无法再放入了。而动态链表则无需考虑这种情况,随时加随时用;
总结:静态链表其实是为了给没有指针或引用的编程语言设计的一种实现单链表功能的方法,这种思想还是需要了解一下的——取他山之石以攻玉!
本系列参考书籍:
《写给大家看的算法书》
《图灵程序设计丛书 算法 第4版》
