牛客OI周赛15-提高组 环球旅行

https://ac.nowcoder.com/acm/contest/4912/A

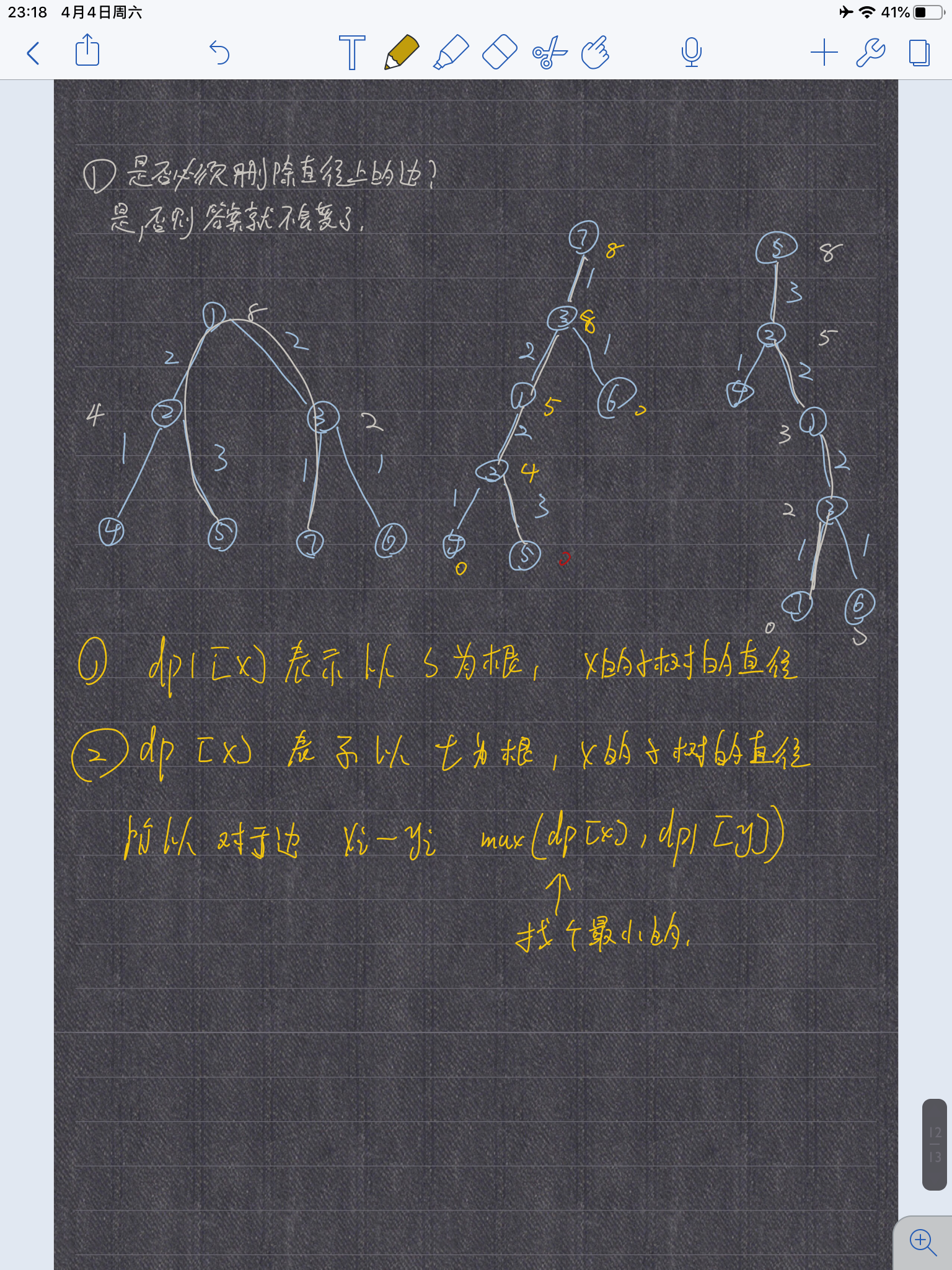
过这个题有个前提，需要知道删除哪条边-------必须是直径上的边

为什么？

如果不删直径上的边答案就不可能减少了，建议多画画试一下

抓住直径两端s和t开始树形DP，

具体看代码吧

#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
#include<queue>
using namespace std;
typedef long long ll;
const int maxn = 1e6 + 77;
ll cns[maxn];
struct Node {	
	int to;
	ll len;
	int nxt;
}G[maxn * 2];
int head[maxn];
int z;
void add(int be, int en,ll len) {
	G[++z].to = en;
	G[z].len = len;
	G[z].nxt = head[be];
	head[be] = z;
}
int n;
ll cs = 0;
int s, t, fa[maxn];
int dfs(int x, int f, int d) {
	if (cs < d) {
		cs = d;
		s = x;
	}
	for (int i = head[x]; i; i = G[i].nxt) {
		int p = G[i].to;
		if (p == f) continue;
		dfs(p, x, d + G[i].len);
	}
	return 0;
}
//-----------------------------------------------------------------------------------------------------------算直径的部分
int son[maxn];//长儿子
ll dp[maxn];//直径
ll dp1[maxn];
ll dep[maxn];//子树到根的最长路

int dfs1(int x, int f) {
	ll s = 0;
	fa[x] = f;

	for (int i = head[x]; i; i = G[i].nxt) {//先找个最长边
		int p = G[i].to;
		ll ln = G[i].len;
		if (p == f) continue;
		dfs1(p, x);
		dp[x] = max(dp[x], dp[p]);//或许子树的直径不过根
		if (s < dep[p] + ln) {
			s = dep[p] + ln;
			son[x] = p;
			dep[x] = s;
		}
	}
	for (int i = head[x]; i; i = G[i].nxt) {//再算子树直径
		int p = G[i].to;
		ll ln = G[i].len;
		if (p == f || p == son[x]) continue;
		dp[x] = max(dp[x], dep[x] + ln + dep[p]);
	}
	dp[x] = max(dp[x], dep[x]);
	return 0;
}


int main() {
	scanf("%d", &n);
	int be, en;
	ll len;
	for (int i = 1; i < n; i++) {
		scanf("%d %d %lld", &be, &en, &len);
		add(be, en, len);
		add(en, be, len);
	}
	dfs(1, -1, 0);
	t = s;int r = s;
	dfs(r, -1, 0);
	//算好直径了
	dfs1(s, -1);
	for (int i = 1; i <= n; i++) {
		dp1[i] = dp[i];
		dp[i] = 0;
		dep[i] = 0;
	}
	dfs1(t, -1);
	//dp1 --- s当根,
	int x = s;
	ll ans = 1e17;

	while (x != -1) {
		int y = fa[x];
		//x用dp，y用dp1
		ll cns = max(dp[x], dp1[y]);
		ans = min(ans, cns);
		x = y;
	}
	printf("%lld
", ans);
	return 0;
}